接收机将换能器接收的微弱回波信号进行检测放大，经处理后送入显示设备。图3-2回声测深仪组成示意图图3-3百米、千米和万米测深仪为了求得实际的水深、对回声测深仪实测的深度数据需施加的改正数，称回声测深仪总改正数。这种改正主要是由于回声测深仪在设计、生产制造和使用过程中产生的误差造成的。回声测深仪按照频率可分为单频测深仪和双频测深仪。......
2023-11-29
多元回归分析原理及应用技术
【摘要】：回归分析原理回归分析方法的基本思想是基于地形地质资料，结合对考察域地应力场产生条件的认识，建立考察域三维有限元模型，计算各种基本影响因素独立作用下的有限元模型“观测值”，并结合一定量的实测值，展开回归计算分析，从而获得模拟整个考察域初始应力场的回归方程。复相关系数可表达为其中:复相关系数r介于0与1之间，r值越接近于1，说明回归效果越好。
(1)回归分析原理
回归分析方法的基本思想是基于地形地质资料，结合对考察域地应力场产生条件的认识，建立考察域三维有限元模型，计算各种基本影响因素独立作用下的有限元模型“观测值”，并结合一定量的实测值，展开回归计算分析，从而获得模拟整个考察域初始应力场的回归方程。
将地应力回归计算值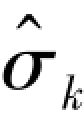
作为因变量，把有限元计算求得的自重应力场和构造应力场相应于实测点的应力计算值作为自变量，则回归方程的形式为
假定有m个观测点，则最小二乘法的残差平方和为
式中: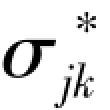
为k观测点j应力分量的观测值。
根据最小二乘法原理，使得S残为最小值的法方程式为
通过求解方程(2.5)，得n个待定回归系数L=(L1，L2，…，Ln)T，则计算域内任一点p的回归初始应力，可由该点各工况有限元计算值叠加而得:
式中:j=1，2，…，6。
(2)回归效果评价方法
为衡量回归效果，可通过计算复相关系数r进行检查;并通过计算偏相关系数Vi(i=1，2，…，n)，检查每个子构造应力场的显著性。
复相关系数可表达为
其中:
复相关系数r介于0与1之间，r值越接近于1，说明回归效果越好。
偏相关系数Vi可表示为
其中:
由于各子构造应力场之间是相容的，其中一个因素的引入必将造成其余因素的退化，因此，需根据偏相关系数将不显著因素剔除。某种工况的偏相关系数越小，说明对实测值的影响越不显著。
有关挤压性围岩隧道变形破坏特性及控制技术的文章
- 详细阅读
-
水的冷却原理及应用技术详细阅读
图7-8水和空气之间的传热过程2.传热量计算蒸发传热量Qe。冷却塔运行过程中，其传热速率的主要影响因素有气水的界面面积、相对流速、接触时间以及冷却范围等。湿球温度代表在当地气温条件下，水可能被冷却的最低温度，也是冷却设备出水温度的理论极限值。......
2023-06-19
-
IDA协议及应用技术分析详细阅读
作为一个单纯的工业以太网协议，IDA涵盖自动化结构中的所有层次，包括设备层。因为Modbus TCP/IP是完全透明的，所以很好地符合IDA。IDA协议建立在组件的基础上，该组件包括了IEC 61449的第一部分体系结构功能块标准，但用IDA的体系结构替代了IEC 61499的模型。除了支持以太网TCP、UDP和IP有关的Web服务的完整套件外，IDA协议规范还包括：基于RTI公司的中间件NDDS的RTPS，Modbus TCP/IP作为工业以太网消息传输协议，IDA通信目标库，实时和安全API。IDA的协议栈如图1-16所示。......
2023-11-20
-
现场总线与工业以太网：应用技术及原理详细阅读
由于标准并未统一，所以对现场总线也有不同的定义。但现场总线的本质含义主要表现在以下6个方面。现场设备互连是基本的要求，只有实现互操作性，用户才能自由地集成FCS。通过网络对现场设备和功能块统一组态，把不同厂商的网络及设备融为一体，构成统一的FCS。......
2023-11-20
-
气割原理及特点分析详细阅读
切割的实质是被切割的材料在氧气中燃烧的过程，并且与借助切割氧的流动而排除熔渣的物理过程相结合。目前最常见的气体火焰切割是氧-乙炔火焰切割和氧-丙烷切割。2）金属的燃点比熔点低，否则不能实现氧气切割而变成熔化切割。铝材虽然氧化反应热很高，但是其氧化物的熔点远高于铝的熔点，并且材料燃点与熔点接近，也属于不可气割的金属。表8-2 常见金属及其氧化物的熔点、燃烧热及其气割性......
2023-07-02
-
迫击炮发射原理及优缺点分析详细阅读
图3-1炮口装填迫击炮弹2.优缺点迫击炮武器系统具有以下优点: 结构简单, 质量轻, 机动性好。由于迫击炮弹从炮口装填, 迫击发火, 射击时无须开关炮闩, 因而发射速度较快。迫击炮的射速每分钟可达几十发。由于迫击炮武器系统的上述优点, 在现代高技术战争中, 迫击炮武器系统仍然是不可替代的。......
2023-06-15
-
CRC校验及应用技术详细阅读
CRC码检错能力强，实现容易，是目前应用最广泛的校验方法之一，CRC校验基本工作原理如图2-14所示。图2-14 CRC校验基本工作原理2）将fxk除以生成多项式G，得式中，R为余数多项式。......
2023-11-22
-
物场分析原理及应用介绍详细阅读
运用物场分析原理创造时，其思考要点如下：1.课题分析分析创造课题的出发点和期望达到的目的。例2－3冷冻机密封检测方案设计：运用物场分析原理求解家用电冰箱中冷冻机密封不良的检测设备的原理方案。因此，本课题运用物场分析原理，主要是将非物场体系补建成非人工检测泄漏的完全物场体系。图2-3过滤器清洗物场体系这个物场虽属完全物场体系，但其功效并不令人满意，打算对此进行改造。......
2023-06-26
相关推荐