图7.7车重为10kN的车辆以静力和动力方式加载的位移响应由图7.7可知，静力荷载作用下，加劲梁的响应为平滑的曲线，而考虑车-桥系统耦合振动的动力加载方式作用下，加劲梁的响应具有一定的波动性，且动力响应的最大值大于静力响应。这表明，车重增加1倍，加劲梁位移响应最大值增加约0.97倍。图7.11不同车重下主梁关键节点的位移响应速度对加劲梁动力响应有一定的影响，但不随着速度的变化而单调增加或减小。......
2023-09-19
桥梁可靠度分析：考虑车重增长的结果
【摘要】：考虑车重的线性增长系数为a，则到运营期的第n年为止，累积疲劳损伤函数可表示为：由此得出100年内顶板-U肋的细节疲劳损伤如图9.5所示。表9.3考虑车重增长的100年后顶板-U肋细节疲劳可靠指标由表9.3可知，当车重的线性增长系数为0.6%时，行车道顶板-U肋细节疲劳可靠指标为1.57，超车道位置处为2.49。
诸多的研究结果表明重型车辆和车辆超载是钢桥疲劳裂纹萌生的重要因素。为了研究车重对南溪长江大桥钢箱梁细节疲劳损伤和寿命的影响，假定随机车流中样本中车辆轴重全部按照b的比例进行增加。由此得出车重增加对疲劳损伤的影响趋势如图9.5所示。考虑车重的线性增长系数为a，则到运营期的第n年为止，累积疲劳损伤函数可表示为：
由此得出100年内顶板-U肋的细节疲劳损伤如图9.5所示。
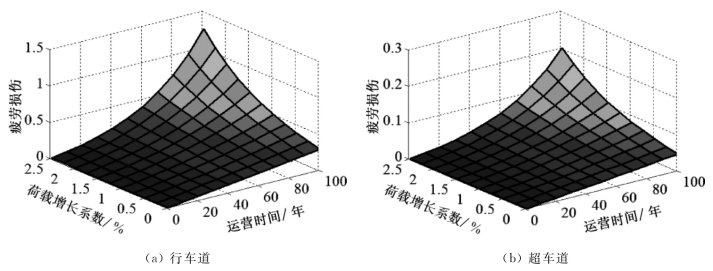
图9.5 车重增加对疲劳损伤的影响
由图9.5可知，随着荷载增长系数b的增加，疲劳损伤呈加速增长趋势。在车重增长系数达到2.2%的时候，行车道的疲劳损伤值D＝1，不能满足规范要求；而超车道的细节疲劳损伤值仅为0.2，还有足够的安全储备。事实上，根据S-N曲线的表达式可知，疲劳损伤D与应力幅值的m次方成正比，在荷载增长时，疲劳损伤将加速增加。因此，在运营期，不仅应控制交通量的增长，还应对车辆荷载的增长进行严格控制。仅考车重增长时，细节疲劳功能函数可表示为：
取车重的增长系数分别为0、1%、2%和3%时，行车道和超车道的顶板-U肋细节疲劳可靠指标在1～100年内的变化趋势如图9.6所示。
图9.6 车重增长对顶板-U肋细节疲劳可靠指标的影响
图9.6中曲线前端具有波动性，这是由于Monte Carlo抽样方法计算可靠指标时，可靠指标较低导致计算结果的变异性较大。由该图可知，随着车重的增长，顶板-U肋细节疲劳可靠指标呈下降趋势，当交通量线性增长系数由0增至0.6%时，顶板-U肋细节疲劳可靠指标在100年后由2.92下降至1.57。这表明了车辆微小的变化量会引起细节疲劳可靠度较大的变化。在桥梁的日常管理中，对车辆重量及超载情况的准确把握有助于对顶板-U肋细节疲劳可靠度做出有效评估。第100年的疲劳可靠指标如表9.3所示。
表9.3 考虑车重增长的100年后顶板-U肋细节疲劳可靠指标
由表9.3可知，当车重的线性增长系数为0.6%时，行车道顶板-U肋细节疲劳可靠指标为1.57，超车道位置处为2.49。
有关桥梁可靠度分析方法与应用的文章
- 详细阅读
-
优化结果分析-桥梁可靠度分析方法与应用详细阅读
取目标体系可靠指标β0＝2，截面及荷载变异系数均为ξ＝0.1，遗传算法优化结果如图5.7所示。图5.7遗传算法迭代过程图由图5.7所示桁架结构遗传算法优化过程可以看出，在第40次种群迭代时，适应度值已经稳定并达到收敛，表明优化过程稳定，优化结果可靠。表5.3不同方法优化结果由表5.3所示的不同体系可靠度约束优化结果可以看出，体系可靠性优化后结构的重量较常规优化方法的大。......
2023-09-19
-
交通量增长对桥梁可靠度影响分析详细阅读
表9.2考虑交通量增长的100年后顶板-U肋细节疲劳可靠度由上述分析可知，交通量的增长对行车道的顶板-U肋细节疲劳损伤有重要的影响，随着运行车辆的增加，细节的疲劳损伤呈加速增长趋势。因此，在运营期应采用有效的方案控制交通量的增长，特别是在行车道位置车辆的通行数量。......
2023-09-19
-
桥梁可靠度分析方法-桥梁可靠度分析方法与应用详细阅读
静定桁架就属于这种结构体系，单元逻辑图如图4.2所示。因尔，从体系可靠度的角度来看，实际的桥梁应尽量避免做成静定结构，条件允许时，应做成具有适当冗余度的超静定结构。超静定结构就是具有这种特性的结构体系。......
2023-09-19
-
桥梁可靠度分析方法与应用-算例分析结果详细阅读
表2.1计算结果比较图2.4算例1迭代过程图2.5算例2迭代过程图中虚线为采用文献［10］的响应面法的迭代过程，实线为改进后的响应面法迭代过程。计算结果表明：算例1的一次二阶矩法结果与文献［13］同种方法给出的结果β＝2.3309，几乎相等；而算例2的一次二阶矩法计算结果不收敛无法得出结果。......
2023-09-19
-
桥梁可靠度分析与应用详细阅读
BS5400规范［4］将常幅疲劳极限ΔσL定义为当循环次数N＝107时对应的容许应力幅值。BS5400规范对不同细节S-N曲线参数规定如表8.1所示。表8.1BS5400规范对疲劳细节S-N曲线参数表8.2BS5400规范的部分疲劳细节分类BS5400规范的特点是规定了常幅疲劳极限，并且基于概率水平给出了结构构造细节在5种失效概率下的S-N曲线。......
2023-09-19
-
桥梁可靠度分析：失效概率与可靠性详细阅读
工程结构可靠度是指在规定的时间内，在规定的条件下，完成预定功能的概率。结构的失效概率是指结构不能完成预定功能的概率，用Pf表示。结构可靠度分析的依据就是根据结构的极限状态计算结构的失效状态的概率。假定式所述两个随机变量的均值和标准差分别为μR、μS和σR、σS，且随机变量均服从正态分布，由此可以获取Z的概率密度函数。......
2023-09-19
-
桥梁可靠度分析中的Possion假定详细阅读
定义若r＞3，则无论结构的响应是宽带过程还是窄带过程，Possion假定均能满足精度要求。下面给出考虑密集车辆占有率的Possion假定动力可靠度表达式：由式可计算出界限跨越率和考虑车辆运行状态的大跨度桥梁位移动力可靠度。......
2023-09-19
相关推荐