根据南溪长江大桥整体有限元模型的计算结果，选取车辆荷载作用下应力变化最大的标准钢箱梁作为疲劳验算的研究对象。表8.8标准梁段主要尺寸参数单位：cm图8.16标准梁段设计图针对基于有限元模拟的细节疲劳特性分析，应对有限元方法进行基本假定。图8.17标准梁段有限元模型随机车流具有随机性特点，而疲劳应力提取是针对确定性的应力时程曲线，如何获取疲劳应力的统计特征也是需要解决的重要问题。......
2023-09-19
南溪长江大桥在随机车流下的疲劳应力分析
【摘要】：表8.15C2车型的轴重均匀设计表单位：kN通过20次有限元计算和雨流计数提取应力循环，并转换为等效应力幅值Seq，通过SVR回归分析可得到C2车型的轴重与Seq的SVR模型。将该车辆样本代入C2车型的SVR模型中可得到各车辆样本对应的钢箱梁细节处的等效应力幅Seq。表8.16某日随机车流作用下细节①的疲劳应力计算结果备注：各车型车辆的数量为全桥单向行驶的数量，即仅考虑半幅通车数量。
以C2车型为例，该车型有AW21和AW22两个轴，按照均匀设计条件，取该两个轴重的均匀设计表U20202（见表8.15），其中20表示20个水平数，2表示2个参数。
表8.15 C2车型的轴重均匀设计表 单位：kN
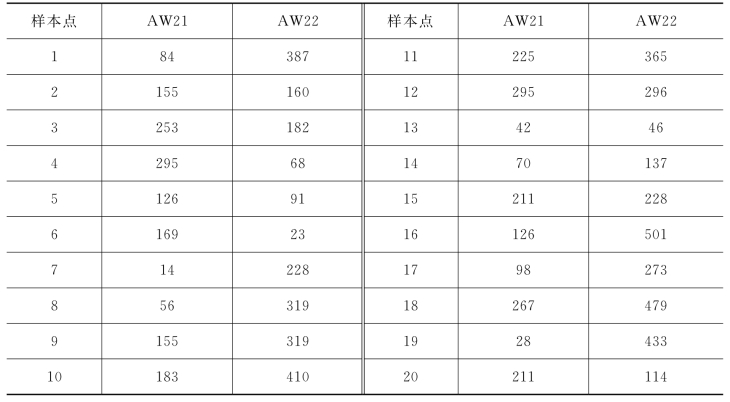
通过20次有限元计算和雨流计数提取应力循环，并转换为等效应力幅值Seq，通过SVR回归分析可得到C2车型的轴重与Seq的SVR模型。其中，设计点如图8.33（a）所示，SVR模型的函数关系如图8.33（b）所示。
图8.33 C2车型的UD-SVR数据
由图8.33可知，均匀设计的样本点能够均匀地布满设计变量空间。随着车轴轮重的增加，细节的等效应力幅值有所增加，且具有一定的非线性。随机抽样某日的随机车流样本，其中C2车型在单向行驶的行车道上数量为254辆，在超车道上数量为26辆。将该车辆样本代入C2车型的SVR模型中可得到各车辆样本对应的钢箱梁细节处的等效应力幅Seq。
在建立每种车型的各轴重与Seq的SVR曲线拟合模型之后，按照第二章随机车流模型生成某日随机车流样本，再由SVR模型得出每辆车的轴重作用下钢桥面板细节的等效应力幅Seq，最后得出日等效应力幅Sdeq，并计算相应的日循环次数Nd。随机抽样某日的随机车流样本，得到的行车道和超车道的细节等效应力幅Seq和应力循环次数计算结果如表8.16所示。
表8.16 某日随机车流作用下细节①的疲劳应力计算结果
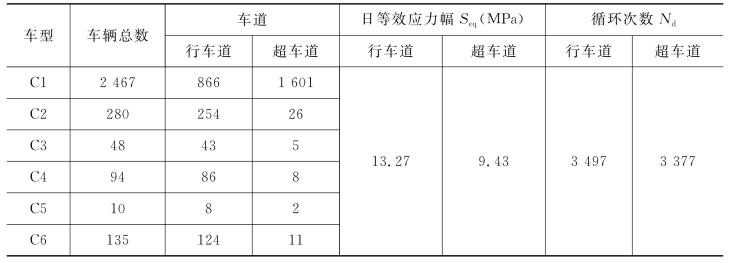
备注：各车型车辆的数量为全桥单向行驶的数量，即仅考虑半幅通车数量。
由表8.16可知，行车道的车辆总数约为超车道的0.8倍，但是行车道的Seq是超车道的1.4倍，行车道的Nd与超车道的几乎相同。这表明，虽然行车道的日通行车辆总数大于超车道数量，但是由于重型货车大部分（C2车型比例为84%）行驶于行车道，该车型对钢桥面板细节的疲劳损伤远大于C1车型，因此相应的等效应力幅值也大于超车道。虽然货车的占有率较低（C2～C5车型的累积值为19%），但是货车在行车道的占有率及车轴数量较多，其产生的钢桥面板的细节疲劳应力循环次数也较C1车型多，综合上述因素，行车道与超车道的Nd值基本相同。
有关桥梁可靠度分析方法与应用的文章
- 详细阅读
-
不同车型疲劳应力分析效详细阅读
每种车型的轴距与轴数均不相同，为研究每种车型作用下钢桥面板细节疲劳应力时程曲线特征，本节将每种车型的车辆分为空载和满载两种情况。在获取各车型的等效应力幅值之后，可采用焊接细节疲劳应力的数学模型进一步分析损伤与疲劳可靠度。本节的研究工作为后面疲劳应力的统计分析奠定了基础。......
2023-09-19
-
结构疲劳应力分析方法及应用详细阅读
疲劳应力分析方法有两种，分别是名义应力法和热点应力法。本书的研究工作是基于名义应力，其分析方法主要有两种，其一是基于疲劳荷载理论对有限元模型加载分析，其二是基于现场实测的疲劳应力时程数据。图8.6基于数值模拟的钢箱梁细节疲劳应力分析流程ANSYS软件中，采用Shell 63号单元的壳单元。因此采用一个梁段的有限元模型模拟实际桥梁的疲劳受力是满足要求的。......
2023-09-19
-
疲劳应力提取方法-桥梁可靠度分析方法详细阅读
结构细节疲劳应力循环的提取是车载作用下钢桥面板疲劳可靠度分析的一个重要步骤。下面将对疲劳应力提取常用方法——雨流计数法进行讨论。雨流计数法又称为塔顶法，是最早由美国的Matsuishi和Endo［15］两位工程师提出的主要应用于工程结构疲劳应力循环提取的方法。图8.3给出了采用雨流计数法基本原理得出的应力循环为1-4-7，2-3-2′和5-6-5′。......
2023-09-19
-
低压断路器操作机构应力分析与疲劳寿命评估详细阅读
低压断路器是低压配电支路的主开关，开断能力以及机械寿命是影响其性能的两个主要因素。低压断路器的机械寿命主要取决于断路器操作机构中零部件的结构形式和加工工艺水平，很多零部件本身的材料和结构具有弹性，部件一方面作绕固定坐标系的运动，另一方面相对自身局部坐标系作弹性变形运动，即部件具有柔性体的特性，会对整个机械系统的运动产生重要影响。......
2023-06-15
-
预应力混凝土受弯构件疲劳验算方法详细阅读
一级裂缝控制等级的预应力混凝土构件的钢筋可不进行疲劳验算。式～式中混凝土压、拉应力以及预应力筋、普通钢筋应力幅计算方法见《混凝土结构设计规范》第6.7.11条。......
2023-08-28
-
钢箱梁细节疲劳应力的概率模型-桥梁可靠度分析详细阅读
车载下钢桥面板细节疲劳损伤与等效应力幅值和相应的日循环次数有关，前者与车型和轴重有关，而与车速和车距的影响不大；后者与车辆的日通行量有关。本节采用高斯混合模型对细节疲劳应力幅和循环次数的概率分布进行拟合，如图8.27～8.30给出了高斯混合模型的拟合结果。由此可知，高斯混合模型能够较好地模拟随机车流作用下疲劳荷载效应的概率分布特征。......
2023-09-19
-
机械应力的分析方法详细阅读
转子所受的机械载荷即为气体爆发压力，是与热负荷共同作用，因此不单独对转子机械应力进行分析。机械载荷作用下，最大应力出现在进气道旁的螺栓孔，此处螺栓预紧力最大。因此对气缸、前端盖、后端盖机械应力分布影响较大的载荷为螺栓预紧力。而对转子而言，转子不直接受螺栓预紧力的影响，其工作过程中仅受到气体爆发压力的作用，在爆发压力的作用下运动，其应力水平较低。......
2023-06-23
相关推荐