车载下钢桥面板细节疲劳损伤与等效应力幅值和相应的日循环次数有关，前者与车型和轴重有关，而与车速和车距的影响不大；后者与车辆的日通行量有关。本节采用高斯混合模型对细节疲劳应力幅和循环次数的概率分布进行拟合，如图8.27～8.30给出了高斯混合模型的拟合结果。由此可知，高斯混合模型能够较好地模拟随机车流作用下疲劳荷载效应的概率分布特征。......
2023-09-19
桥梁细节疲劳损伤概率模型-钢箱梁
【摘要】：由300组随机车流样本分析得到的钢箱梁细节日疲劳损伤Dd的概率模型如图8.31、8.32所示。图8.31行车道的细节疲劳损伤概率模型图8.32超车道的细节疲劳损伤概率模型由图8.31和8.32可知，行车道和超车道的日疲劳损伤均呈单峰偏态分布。表8.14南溪长江大桥钢桥面板细节疲劳荷载效应的概率参数高斯混合模型可适用于建立随机车流作用下钢箱梁细节疲劳应力及疲劳损伤的概率模型。等效疲劳应力及日应力循环次数呈多峰分布，疲劳损伤呈单峰的偏态分布。
引入车辆的轮迹横向分布系数e＝0.76，随机车流作用下细节①的日累积损伤值如表8.13所示。
表8.13 随机车流下钢箱梁细节的疲劳损伤计算表
由表8.13可知，行车道的Seq大于超车道，而行车道的Nd均值略小于超车道，但行车道的日损伤值约为超车道日损伤值的5倍。根据细节①的日损伤值平均值，可得出行车道的疲劳寿命为811年，超车道的疲劳寿命为4 027年。
行车道的车辆较少，但是行车道的等效应力幅值比超车道的高。C1车型的65.36%行驶在超车道，而只有36.64%行驶在行车道，超车道数量是行车道数量的1.8倍；而C2～C6中大多数车辆均行驶在行车道，虽然行车道的车辆数量较少（约是超车道的0.57倍），但行车道的重载车辆对钢箱梁细节等效应力幅值较大。行车道的寿命约为超车道的1／5。由300组随机车流样本分析得到的钢箱梁细节日疲劳损伤Dd的概率模型如图8.31、8.32所示。
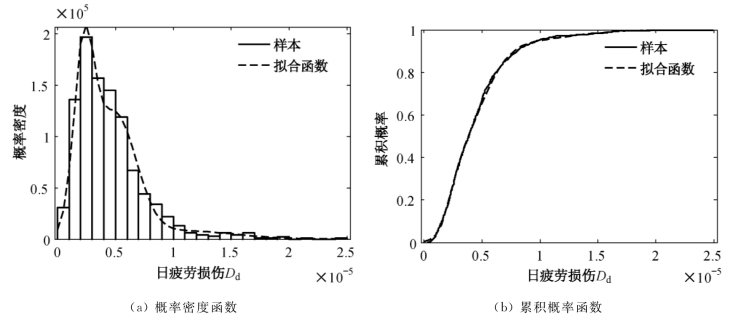
图8.31 行车道的细节疲劳损伤概率模型
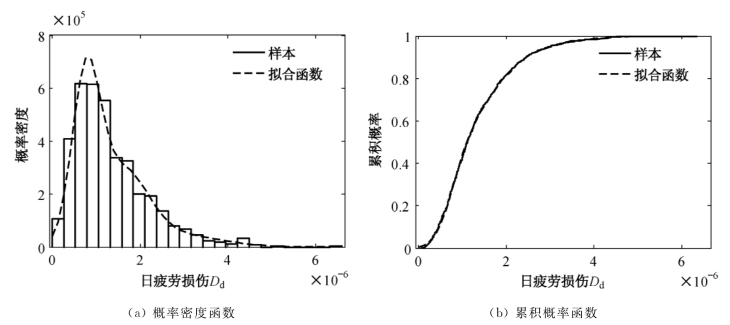
图8.32 超车道的细节疲劳损伤概率模型
由图8.31和8.32可知，行车道和超车道的日疲劳损伤均呈单峰偏态分布。采用GMM模型可较好地拟合其概率密度和概率分布函数。行车道细节的日疲劳损伤概率密度峰值处的日疲劳损伤值约为4×10-6，超车道处的约为8.5×10-8，相应参数如表8.14所示。
表8.14 南溪长江大桥钢桥面板细节疲劳荷载效应的概率参数
高斯混合模型可适用于建立随机车流作用下钢箱梁细节疲劳应力及疲劳损伤的概率模型。等效疲劳应力及日应力循环次数呈多峰分布，疲劳损伤呈单峰的偏态分布。随机车流的引入为细节疲劳损伤概率模型的建立提供了有利条件，而建立疲劳损伤概率模型之后即可通过功能函数分析细节疲劳可靠度。总之，细节疲劳损伤概率分析为其疲劳可靠度评估提供了有利条件。
有关桥梁可靠度分析方法与应用的文章
- 详细阅读
-
结构损伤多尺度模拟与分析：桥梁钢箱梁疲劳损伤详细阅读
桥梁上的正常服役荷载一般在结构中产生高周疲劳损伤的累积，而强震台风等灾害荷载会导致结构中已累积损伤的高应力区域在短时间内发生低周疲劳损伤演化。因此，在桥梁钢箱梁结构的疲劳损伤演化过程分析中，首先要解决如何模拟高、低周疲劳交互作用下的疲劳损伤演化过程的问题，建立疲劳损伤演化过程中群体短裂纹和长裂纹共同演化行为的本构描述。......
2023-08-26
-
大跨桥梁钢箱梁疲劳损伤分析方法详细阅读
大跨桥梁作为在复杂环境下长期服役的工程结构，其中的疲劳损伤累积过程是由多个因素耦合作用且跨尺度演化的过程。为模拟在此主要作用机理下的桥梁结构的疲劳损伤演化过程和剩余寿命，还须进一步发展模拟桥梁结构在服役荷载与极端荷载交互作用下的疲劳损伤跨尺度演化过程的多尺度有限元方法。当疲劳损伤演化处于长期缓慢累积过程时，如在结构服役的初期并且未遭受极端灾害荷载时，为提高疲劳损伤分析的效率，可在增量型平......
2023-08-26
-
钢箱梁细节疲劳寿命分析：《桥梁可靠度分析方法详细阅读
目标可靠指标下悬索桥钢箱梁细节疲劳寿命的研究结果表明，随着交通量和车重线性增长系数的增加，目标可靠指标下顶板-U肋细节的疲劳寿命逐渐降低。在运营期，应通过对车流量的监测数据定期更新车流量统计数据库，并建立预测车流量模型，才能对悬索桥钢箱梁细节疲劳可靠度做出准确的评估。当交通量增长系数或车重增长系数超出既定范围时，应对交通量进行管制，或对钢箱梁进行检测加固，以确保悬索桥钢箱梁细节疲劳可靠度水平。......
2023-09-19
-
钢桥疲劳损伤概率建模方法详细阅读
在得到每种车型的SVR回归模型后，即可快速得出每个固定车型样本对应的疲劳应力。图8.13基于UD-SVR方法的随机车流下钢箱梁疲劳应力的分析流程图针对随机车流作用下钢桥面板疲劳应力分析，若采用第四章中整体模型中的加载方式进行分析，由于局部模型中单元数量超过1万个，则需花费极多的运算时间。......
2023-09-19
-
桥梁疲劳损伤分析方法-钢桥改进技术详细阅读
目前，钢桥疲劳损伤有三种分析模型：概率S-N曲线模型、概率断裂力学模型和随机有限元模型。图8.1典型的S-N曲线此后，Fisher［2］通过对多座钢桥疲劳试验数据分析，为各国钢桥疲劳设计规范中的S-N曲线提供了研究基础。......
2023-09-19
-
昂船洲大桥钢箱梁结构疲劳损伤多尺度跨层次演化详细阅读
图8.17昂船洲大桥单一宏观尺度下的结构模型利用如图8.17所示模型进行桥梁结构在正常服役的交通荷载下的疲劳损伤演化过程模拟，发现桥梁跨中部位承受的内力最大，确定跨中部位的桥面板为钢箱梁疲劳损伤的关键截面。包含了第一、二类计算区域的昂船洲大桥疲劳损伤多尺度分析模型如图8.21所示。利用上述模型分析昂船洲大桥在正常服役的交通荷载作用下疲劳损伤多尺度跨层次演化的过程，可得到......
2023-08-26
-
钢箱梁的加工和安装流程详解详细阅读
5.4.2.1主桥面分段方案根据钢箱梁内部结构、板厚分布、锚点设置及梁段运输、现场安装以及制造能力等综合情况，全桥纵桥向共分为29 个节段，如图5 -31 所示。......
2023-07-01
相关推荐