目前,钢桥疲劳损伤有三种分析模型:概率S-N曲线模型、概率断裂力学模型和随机有限元模型。图8.1典型的S-N曲线此后,Fisher[2]通过对多座钢桥疲劳试验数据分析,为各国钢桥疲劳设计规范中的S-N曲线提供了研究基础。......
2023-09-19
随机车流作用下钢桥面板疲劳损伤与寿命评估在分析过程中面临的一个重要问题是:由于有限元模型对构造细部划分单元较多,在较小的荷载步和巨大的车流量情况下,需要巨大的时程分析时间。若采用时程分析方法计算随机车流作用下的钢桥面板细节疲劳应力,则需要大量的计算时间。事实上,随机车流是由大量的随机车辆样本组成的,行车间距(均值大于800m)远远大于车辆的长度以及单个钢箱梁的长度(12.8m),更小于上述影响线分析中得到的影响线范围(两个横隔板的间距(3.8m))。因此可将随机车流中的每个车辆独立出来,分析计算每种车型通过钢箱梁时对细节产生的疲劳应力,这样省掉了两车之间的车距所占用的分析时间。虽然这种做法省去了随机车流时程分析的大量分析时间(假定车距为100m,车长为10m,则节省分析时间为90%),但是,这样又面临着另一个问题,大量的车辆样本时程分析依然耗时(每个车辆过桥分析时间为4 min,日通行车辆样本约6 500个,分析时间约633h),而概率分析方面需要更多的随机车流样本,这种方法基本行不通。
为了在保证随机车流作用下结构细节疲劳应力计算精度的同时提高分析效率,本节将提出一种基于UD-SVR(均匀设计-支持向量回归)的联合分析方法,其中,UD方法用于设计每种车型的轴重样本点,SVR方法用于拟合各轴重与疲劳应力的函数关系式。在得到每种车型的SVR回归模型后,即可快速得出每个固定车型样本对应的疲劳应力。本节的分析流程如图8.13所示。
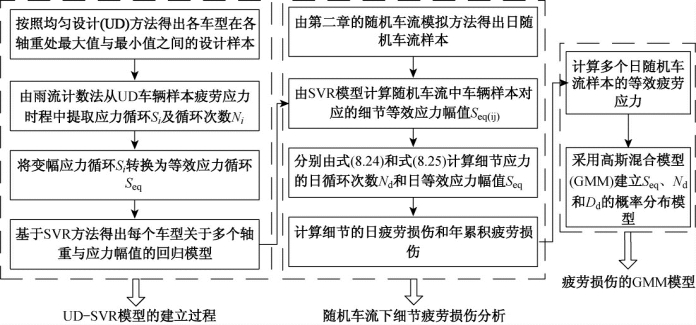
图8.13 基于UD-SVR方法的随机车流下钢箱梁疲劳应力的分析流程图
针对随机车流作用下钢桥面板疲劳应力分析,若采用第四章中整体模型中的加载方式进行分析,由于局部模型中单元数量超过1万个,则需花费极多的运算时间。事实上,由双轮荷载作用下钢桥面板的应力分布云图可知,车载下钢桥面板的疲劳应力幅值仅在车轮能过细节应力附近时才会出现,而且有效影响线仅在该幅值附近,因此可忽略随机车流中两辆车的行车间距,采用“单车过桥”的形式加载,这样大大减小了行车间距的时间。
由于随机车流中,每个车型的轴重是由Monte Carlo随机抽样得出,每个样本的轴重均不相同,若将每辆车的轴重都进行一次有限元分析,则需要巨大的时间完成每天的随机样本车辆的加载,而且针对于疲劳应力的统计分析,则需要100天以上的随机车流样本加载,采用上述方式几乎不可能实现疲劳可靠度的分析。事实上,虽然针对每种车型的每个随机样本,其轴重均在一定的范围内变化,且轴重与结构细节的等效应力幅值存在一定的函数关系,可以通过大量的试验数据拟合轴重与细节等效应力幅值的函数式。
目前,常用的函数拟合方法有最小二乘法、响应面法和神经网络方法等。每种方法均有各自的适用范围,也有一定的缺点,比如神经网络方法可以采用高斯函数为基函数,拟合出具有高次非线性函数关系式,但该方法的泛化能力较差,且训练过程中易陷入局部最优。神经网络受到网络结构复杂性和样本复杂性的影响较大[28],其主要缺点有两个:首先,低泛化能力和过学习限制了其对复杂函数的拟合能力;其次,缺乏系统的理论支持。然而以统计学理论为基础的支持向量方法完全避免了神经网络方法的上述缺点,在模式识别、函数拟合和结构可靠度分析中得到了广泛的应用[29]。
样本点的选取是影响函数拟合精度和计算效率的关键因素,若样本点选取太差,则函数拟合精度较低,而计算效率较差,因此采用一定样本点选取策略较为重要。常用的样本点设计方法主要有正交设计、超拉丁立方设计和均匀设计(UD)等。本书选取了在多因素及多水平下较为优秀的UD作为样本点设计方法。
1.均匀设计方法
均匀设计(UD)是由我国著名的数学家方开泰共同提出的新型实验设计方法,也是用设计好的表格安排实验的方法。均匀设计在理论上有了很多新发展,并在可靠度领域中得到了应用。相比于正交设计在挑选代表点时有两个特点:均匀分散和整齐可比。均匀设计为了减少样本数目,只考虑其在设计参数范围内的变异性。均匀设计的目标就是将设计点均匀地分布于整个设计空间内。均匀设计的优点就是在实验因素和水平因素相同的情况下,比正交设计和超拉丁立方设计的实验次数更少,因此适用于多因素和多水平而又限制次数的实验设计。从统计学角度看,均匀设计实验结果需要进行统计回归分析,这对分析人员的统计知识有更高的要求。
Tang等[30]编制的DPS(数据处理系统)可以生成多水平和多因素的均匀设计样本点,该软件为均匀设计的推广和应用提供了有利条件。
2.SVR模型
SVM最早是由Vapnik[31]提出的一种机器学习方法,也是一种专门研究小样本情况下机器学习规律的理论,主要有支持向量分类(SVC)和支持向量回归(SVR)两种算法。支持向量机主要用于模式识别和分类问题,Asa Ben-Hur[32]通过采用支持向量机技术从随机变量的原始空间映射到高维特征空间来实现聚类分析。Drucher[33]的研究结果表明,支持向量回归的性能和精度不依赖于随机变量的空间维数,所以在高维空间内显示出了极大的优越性。Suykens[34]提出了最小二乘支持向量机(LS-SVM),该方法在处理大规模数据方面采用了共轭梯度算法,其学习效率非常高。支持向量机在可靠度分析中得到了较好地应用,诸多学者[35]对支持向量机进行了改进,提高了结构可靠度的计算效率和精度。然而,支持向量机在交通量预测方面的应用微乎其微。
SVR学习理论主要是通过ε敏感函数来控制SVR模型的拟合误差。
![]()
式中,g(x)为SVR模型的预测值;y为结构响应的输入值;e为误差控制精度。由此可知,若g(x)比y值大,则通过该函数对支持向量进行筛选。该函数的基本原理如图8.14所示。
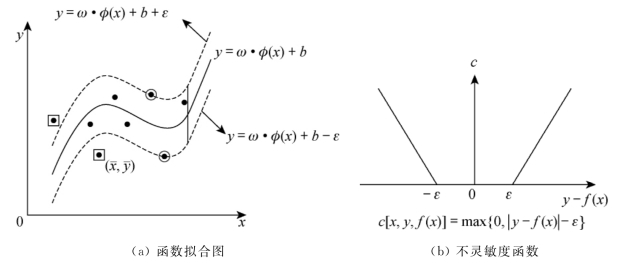
图8.14 SVR结构图
在实际工程结构中,随机变量值与结构响应值具有一定的非线性。将高斯函数作为SVR模型的基函数,则SVR模型的数学表达式为:
g(x)=w·φ(x)+b (8.27)
式中,x为随机变量;φ(x)为高斯函数;w为各高斯函数的权重;b为偏差。引入最小二乘算法(LS),可得到约束优化函数:
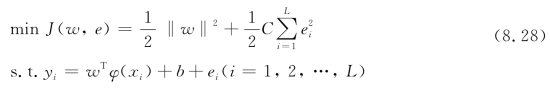
式中,C为归一化参数;e为误差向量。通过引入如式(5.21)所示的拉格朗日函数可求解式(8.28)中的参数最优值。
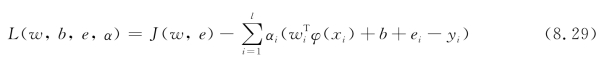
式中,αi为拉格朗日乘子,可由文献[37]所示的KKT条件得出。由式(8.27)可得到SVR模型的函数表达式:
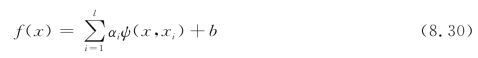
为了提高建立SVR模型的效率与精度,可通过对输入样本点及SVR模型参数进行优化。在样本点选取方面,可采用均匀设计方法。文献[36]给出了优化式(8.28)中的C、σ和ε等参数和优化方法。
支持向量回归是建立在结构风险最小化原则的基础上,它既考虑了训练样本的拟合性,又考虑了训练样本的复杂性,具有较好的拟合效果。但模型中的参数选择是很重要的,它将直接影响到支持向量回归的效果。如图8.15给出了SVR模型的建立流程。
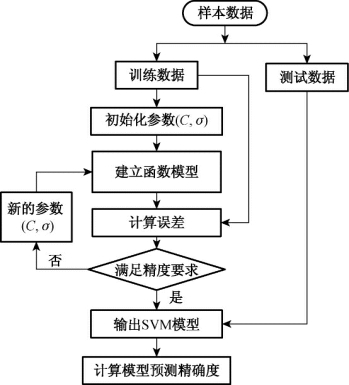
图8.15 SVR模型建立的流程图
3.UD-SVR在随机车流下钢桥面板疲劳应力的分析步骤
基于UD-SVR方法的随机车流下钢桥面板的疲劳应力分析的具体步骤为:
(1)采用统计分析软件(本书采用DPS数据处理系统)生成服从Unnm的设计样本表,其中,U表示均匀设计,n为设计的样本数量,m表示随机变量的个数。
(2)确定每个车型各轴重的分布区间,根据均匀设计样本表生成该区间内的随机车辆样本。
(3)通过有限元加载分析得出随机样本车辆下细节的应力时程,并通过雨流计数方法提取应力幅值,从而得出每个车辆样本作用下细节的应力幅值。
(4)在MATLAB平台,编制SVR程序,计算每种车型的车辆样本作用下桥面板焊接细节的应力幅值,然后由图8.15所示的流程图得出每种车型SVR模型。
(5)根据第二章所述日随机车流样本,将各车道下的车辆分别输入对应车型的SVR模型中,输出相应的等效应力幅值。同时根据各车型的数量计算日等效应力幅值Seq对应的日循环次数Nd。
(6)根据S-N强度曲线和线性累积损伤准则计算细节的日疲劳损伤值Dd,并计算当疲劳损伤值D=1时的疲劳寿命值。
4.疲劳损伤公式
根据S-N曲线和线性累积损伤准则可得到细节的日疲劳损伤为:

不考虑交通量增长和车重增长的桥梁服役时间为Y年的累积损伤为:

值得说明的是,由于随机车流样本具有随机性,因此Nd、Seq、Dd和D(Y)在每次计算中均有不同的结果。通过大量的随机车流样本计算可得到其概率分布函数,这为疲劳可靠度分析奠定了基础。
有关桥梁可靠度分析方法与应用的文章

目前,钢桥疲劳损伤有三种分析模型:概率S-N曲线模型、概率断裂力学模型和随机有限元模型。图8.1典型的S-N曲线此后,Fisher[2]通过对多座钢桥疲劳试验数据分析,为各国钢桥疲劳设计规范中的S-N曲线提供了研究基础。......
2023-09-19

由300组随机车流样本分析得到的钢箱梁细节日疲劳损伤Dd的概率模型如图8.31、8.32所示。图8.31行车道的细节疲劳损伤概率模型图8.32超车道的细节疲劳损伤概率模型由图8.31和8.32可知,行车道和超车道的日疲劳损伤均呈单峰偏态分布。表8.14南溪长江大桥钢桥面板细节疲劳荷载效应的概率参数高斯混合模型可适用于建立随机车流作用下钢箱梁细节疲劳应力及疲劳损伤的概率模型。等效疲劳应力及日应力循环次数呈多峰分布,疲劳损伤呈单峰的偏态分布。......
2023-09-19

目前,钢桥疲劳性研究的基础是S-N曲线,S-N曲线为结构所受应力幅值与应力循环次数之间的关系。根据S-N曲线可以确定材料的疲劳性能。长安大学的陈一馨[21]对顶板-U 形肋纵向焊缝和顶板-横隔板焊缝处的构造细节进行了疲劳试验研究,扩展了英国BS5400规范的S-N曲线至高寿命区域。为了考虑车辆荷载作用下钢桥面板细节疲劳应力中的高频低幅特征,本节将在多个国家规范中对S-N曲线的定义和低应力循环处理方法展开讨论。......
2023-09-19

大跨桥梁作为在复杂环境下长期服役的工程结构,其中的疲劳损伤累积过程是由多个因素耦合作用且跨尺度演化的过程。为模拟在此主要作用机理下的桥梁结构的疲劳损伤演化过程和剩余寿命,还须进一步发展模拟桥梁结构在服役荷载与极端荷载交互作用下的疲劳损伤跨尺度演化过程的多尺度有限元方法。当疲劳损伤演化处于长期缓慢累积过程时,如在结构服役的初期并且未遭受极端灾害荷载时,为提高疲劳损伤分析的效率,可在增量型平......
2023-08-26

桥梁上的正常服役荷载一般在结构中产生高周疲劳损伤的累积,而强震台风等灾害荷载会导致结构中已累积损伤的高应力区域在短时间内发生低周疲劳损伤演化。因此,在桥梁钢箱梁结构的疲劳损伤演化过程分析中,首先要解决如何模拟高、低周疲劳交互作用下的疲劳损伤演化过程的问题,建立疲劳损伤演化过程中群体短裂纹和长裂纹共同演化行为的本构描述。......
2023-08-26

目前,国内外钢桥设计主要采用容许应力法和半概率极限状态设计法两种。我国《钢木规范》在钢桥各类构件的计算中均采用容许应力法。在《钢木规范》第1.2.5条~第1.2.9条中,可查到相应的容许应力值。根据《钢木规范》第1.2.10条,验算结构在各种荷载作用下的强度和稳定性时,基本钢材和各种连接的容许应力应乘以表7.3-1的提高系数k。验算挠度时,《钢木规范》第1.1.5条规定:由汽车荷载所引起的竖向挠度,不应超过表7.3-2所列的容许值。......
2023-08-28

车载下钢桥面板细节疲劳损伤与等效应力幅值和相应的日循环次数有关,前者与车型和轴重有关,而与车速和车距的影响不大;后者与车辆的日通行量有关。本节采用高斯混合模型对细节疲劳应力幅和循环次数的概率分布进行拟合,如图8.27~8.30给出了高斯混合模型的拟合结果。由此可知,高斯混合模型能够较好地模拟随机车流作用下疲劳荷载效应的概率分布特征。......
2023-09-19
相关推荐