Rocco等［4］提出了联合SVM和MCS求解结构可靠度的方法。SVM在结构体系可靠度分析中的应用较少。为了发展工程结构体系可靠度理论与方法在桥梁安全评估中的应用，本章将建立桥梁结构体系可靠度分析的简化模型，总结现有结构体系可靠度分析方法，提出基于支持向量机的桥梁结构可靠度分析方法，最后采用两个算例分析表明支持向量机在桥梁结构体系可靠度评估中的应用。......
2025-09-30
首超可靠度计算方法及应用
【摘要】：表7.11基于Passion假定的界限跨越率根据Possion假定，对南溪长江大桥在随机车流作用下的动力可靠度进行计算，可得到不同运行状态下的动力可靠度。图7.21随机车流作用下加劲梁的首超动力可靠指标为了对比Markov过程与Possion对本算例的计算结果的误差，可得到Markov过程的跨越率，参数如表7.12所示。
按照中国公路桥梁技术状态评定标准［5］和公路悬索桥设计规范［6］的规定，主梁的位移界限值b＝L／300＝2.73m。该界限值下的的界限跨越率如表7.11所示。
表7.11 基于Passion假定的界限跨越率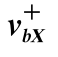
根据Possion假定，对南溪长江大桥在随机车流作用下的动力可靠度进行计算，可得到不同运行状态下的动力可靠度。
由图7.21可知，南溪长江大桥加劲梁的位移动力可靠指标在L／4的位置小于L／2的位置。在加劲梁的L／4处，稀疏运行状态下动力可靠指标由8.21下降至7.81，密集运行状态下动力可靠指标由4.78下降至3.75。
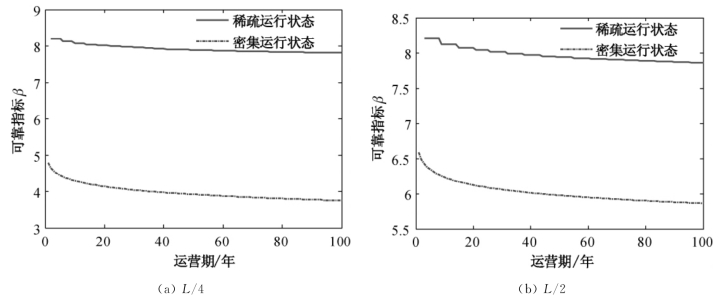
图7.21 随机车流作用下加劲梁的首超动力可靠指标
为了对比Markov过程与Possion对本算例的计算结果的误差，可得到Markov过程的跨越率，参数如表7.12所示。
表7.12 基于Markov假定的界限跨越率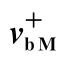
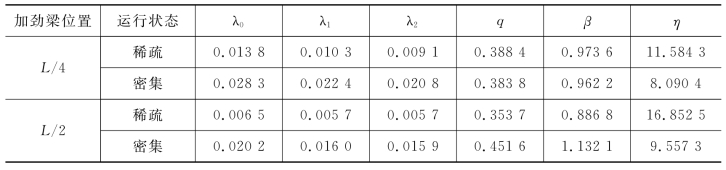
将表7.12的数据代入Rice公式可得到在b＝2.73处的界限跨越率比值，如表7.13所示。
表7.13 界限跨越率比值(https://www.chuimin.cn)
由表7.13可知，Possion假定和Markov假定下的界限跨越率基本相同，仅在密集运行状态下Markov的跨越率稍小。因此，为了分析方便，下文的界限跨越率统一采用Possion假定。
实际交通量随时间逐步增长，动力响应的均方根也随之增大，因此，交通量对动力可靠指标具有一定影响。密集状态车辆所占比例增加后，当日的总交通量也会随之增长，因此可采用密集状态车辆所占当日总交通量的比例来模拟交通量增长。在100年内，密集状态车辆不同占有率下的可靠指标的变化如图7.22所示。
图7.22 密集车辆占有率对可靠指标的影响
由图7.22可知，随着密集车辆占有率的增长，加劲梁位移动力可靠指标呈下降趋势。随着运营时间的增加，悬索桥动力可靠指标下降趋势较缓。在不考虑桥梁结构抗力退化的情况下，随机车流作用下悬索桥主梁位移超限失效事件主要由密集运行车辆荷载的存在引起，且随着密集运行车辆的增长其可靠指标下降趋势减缓。这表明密集运行车辆的存在是导致悬索桥位移动力可靠度降低的重要因素。
根据监测系统的车辆数据可知密集运行状态车辆占单日车辆总数的2.15%（即a）［7］。为了能够反映真实的交通量，取实际运行状态车辆中密集状态车辆为0.8a、a和1.2a，可得出100年内主梁L／4跨节点位移动力可靠指标随时间变化趋势如图7.23所示。由图可知，密集运行车辆的占有率对悬索桥加劲梁动力可靠度有较大的影响，且随着运营时间的增长，影响较大。
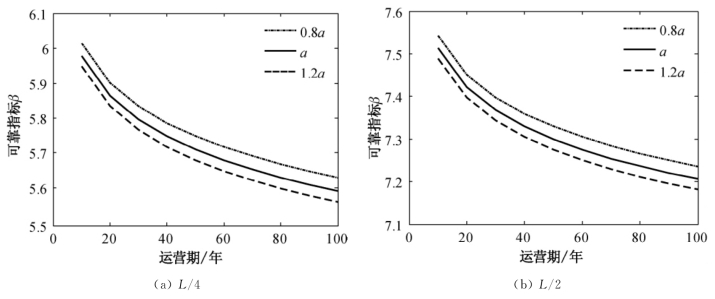
图7.23 密集运行车辆占有率的变化对可靠指标的影响
以某主跨为820m的悬索桥为工程背景，基于位移首超破坏准则对随机车流作用下加劲梁的动力可靠度进行了研究，分析了Possion假定和Markov假定对界限跨越率的影响，分别讨论了车辆运行状态对动力可靠指标的影响规律。研究结果表明，由于车辆荷载作用下悬索桥加劲梁的位移响应均值（密集运行状态下约为0.16m）远小于界限值（1.37m），且加劲梁的位移响应为宽带随机过程，因此Possion和Markov假定下的界限跨越率v+b基本相等。加劲梁的位移首超破坏主要出现在加劲梁的L／4位置，且密集运行状态下加劲梁的界限跨越率远大于稀疏运行状态，这表明悬索桥加劲梁位移失效事件主要是由密集运行车辆的存在而引起。
相关文章
- 详细阅读
-
桥梁可靠度分析方法-桥梁可靠度分析方法与应用详细阅读
静定桁架就属于这种结构体系，单元逻辑图如图4.2所示。因尔，从体系可靠度的角度来看，实际的桥梁应尽量避免做成静定结构，条件允许时，应做成具有适当冗余度的超静定结构。超静定结构就是具有这种特性的结构体系。......
2025-09-30
-
Markov假定在桥梁可靠度分析中的应用详细阅读
由此可得到基于Markov过程的动力可靠度表达式：通过上述分析可以发现，不同界限跨越假定下的动力可靠度计算公式具有相同的表达形式，差别主要表现在单位时间内响应值跨越界限的期望不同。上述内容主要基于首超破坏准则建立了结构动力响应首超可靠度的数学模型，分别基于位移跨越次数的Possion分布和Markov给出了考虑车辆运行状态的动力可靠度表达式。......
2025-09-30
-
桥梁可靠度分析方法—综述与应用详细阅读
把结构可靠度引入到工程结构优化设计数学模型中，根据现有的资源及结构功能要求，选取合适的目标可靠指标为约束条件，并采用遗传算法求解，既可以实现此类工程结构优化设计，又能保证结构在使用过程中的安全性。文献［8］建立了半刚性连接框架的拓扑模型，并结合遗传算法进行了基于体系可靠度的结构优化设计，认为不考虑可靠度的优化设计结构存在安全隐患。......
2025-09-30
-
桥梁可靠度分析方法与应用：突破破坏准则详细阅读
首次超越破坏表示为结构的动力响应首次超越临界值或安全界限的事件。下面以单侧界限为例对首次超越破坏模型进行阐述。根据随机过程定义，式又可表示为：Pr＝P｛max［x］≤b，0＜t≤T｝式中，max［x］为时间（0，T］内随机过程x（t）的最大值。直接求解式较为困难，可以通过对界限的交叉次数进行统计分析。该公式为基于首次超越破坏准则的结构动力可靠度分析奠定了基础。......
2025-09-30
-
桥梁可靠度分析软件流程及功能详细阅读
图3.5结构体系可靠性评估软件的流程图基于MATLAB语言平台的GUI功能，将图3.5所示的计算流程编制评估软件，主界面如图3.6所示。为了帮助用户更好地使用该软件，特编写用户手册。本软件采用纯M文件代码编写，因此界面不受GUI版本限制。图3.6中，菜单栏从左至右分别为：“参数”、“迭代数据”、“RSM数据”、“ANN数据”和“帮助”。“串关联”表示各构件之间是串关联关系。表3.2操作键及功能......
2025-09-30
-
桥梁可靠度分析方法与应用-验算点法详细阅读
针对中心点法计算精度较低的问题，Hasofer和Lind等提出了验算点法［2］。图2.1当量正态化示意图图2.2n维空间的极限状态曲面图假设受n个非正态分布随机变量影响的结构极限状态方程为：Z＝g（X1，X2，…由公式（2.3）、和联立可求解可靠指标β和验算点。值得注意的是，在由Newton迭代法求出β值后，按式计算原坐标系中的验算点时，应区分正态分布和非态分布参数的μXi值。......
2025-09-30
-
优化结果分析-桥梁可靠度分析方法与应用详细阅读
取目标体系可靠指标β0＝2，截面及荷载变异系数均为ξ＝0.1，遗传算法优化结果如图5.7所示。图5.7遗传算法迭代过程图由图5.7所示桁架结构遗传算法优化过程可以看出，在第40次种群迭代时，适应度值已经稳定并达到收敛，表明优化过程稳定，优化结果可靠。表5.3不同方法优化结果由表5.3所示的不同体系可靠度约束优化结果可以看出，体系可靠性优化后结构的重量较常规优化方法的大。......
2025-09-30
相关推荐