一般的MC法用于高度非线性的极限状态曲面或者随机变量维数较高的情况，使用在笛卡儿坐标下的抽样模拟法效率较低，计算耗时较多。因此，Ditlevsen、Olesen、Mohr提出了在标准正态空间中极坐标下进行抽样的方向抽样MC法。③重复步骤①和②直到N次，利用式估计失效概率。对于极限状态曲面接近球面的情况，方向抽样MC法比笛卡尔坐标空间的MC法占较大的优势，若计算接近平面的极限状态曲面时，则无优势。......
2025-09-30
桥梁可靠度分析与车重的影响
【摘要】：图7.7车重为10kN的车辆以静力和动力方式加载的位移响应由图7.7可知，静力荷载作用下，加劲梁的响应为平滑的曲线，而考虑车-桥系统耦合振动的动力加载方式作用下，加劲梁的响应具有一定的波动性，且动力响应的最大值大于静力响应。这表明，车重增加1倍，加劲梁位移响应最大值增加约0.97倍。图7.11不同车重下主梁关键节点的位移响应速度对加劲梁动力响应有一定的影响，但不随着速度的变化而单调增加或减小。
在了解悬索桥动力响应特征之后，即可结合车-桥系统振动理论与方法对车载下悬索桥的动力响应进行展开分析。本节将对单车过桥的动力响应进行分析，主要从车辆加载方式、桥梁参数和车辆参数对加劲梁动力响应的影响这三个方面展开分析。
首先分析车辆荷载以静力和动力加载方式对加劲梁动力响应的影响。取车辆的重量为100kN，在静力荷载Fs和动力荷载Fd作用下，加劲梁的位移响应如图7.7所示。
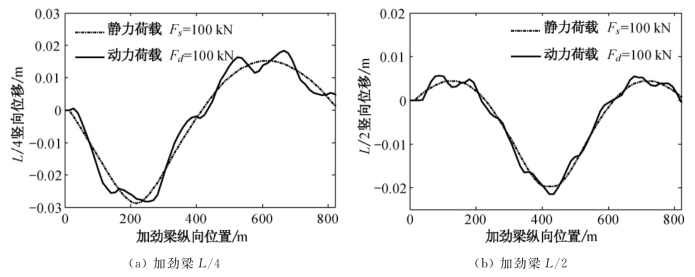
图7.7 车重为10kN的车辆以静力和动力方式加载的位移响应
由图7.7可知，静力荷载作用下，加劲梁的响应为平滑的曲线，而考虑车-桥系统耦合振动的动力加载方式作用下，加劲梁的响应具有一定的波动性，且动力响应的最大值大于静力响应。动力方式加载下加劲梁的速度和加速度响应如图7.8所示。
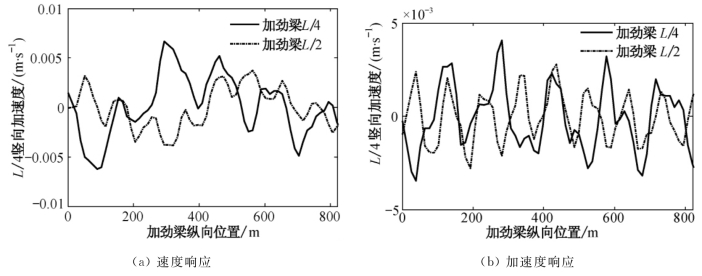
图7.8 车重为10kN的动力荷载作用下响应时程曲线
时间步长的选择直接影响到计算的精度与效率，时间步长过小则使得计算时间较长，时间步长过大则无法保证计算精度。根据随机车流统计车速参数，车速均值在66～87 km／h之间，南溪长江大桥主跨为820m，单车过桥的时间约为41s，车辆通过每片钢箱梁的时间约为0.64s，把通过每个钢箱梁的时间取为10小段，则计算时间步长为0.064s，每辆车通过桥梁共计640个荷载步。
在有限元模拟时需要做一些假定，本书假定汽车车轮与桥面始终接触，不考虑路面平整度的影响，桥梁的阻尼为Rayleigh模型阻尼。C3车型的参数如表7.6所示。
表7.6 C3车型参数表
车辆以不同的行车速度通过桥梁时对桥梁各个节点产生的动力响应值均不同，为了分析上述参数对桥梁动力响应的影响，现将各参数进行以下分析。根据表7.6所示车辆参数，假定以v0＝72km／h的速度通过南溪长江大桥，则L／4和L／2处的位移响应时程如图7.9和表7.7所示。
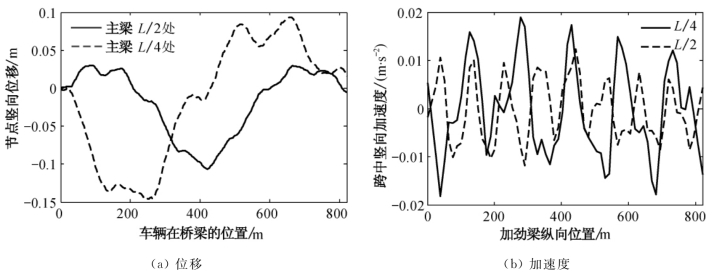
图7.9 C3车型通过桥梁时桥梁节点的响应
表7.7 C3车型通过桥梁时桥梁节点的响应表(https://www.chuimin.cn)
由此可知，在相同的v0＝72km／h的条件下，悬索桥主梁L／4和L／2处的节点位移、速度和加速度响应规律和峰值均不相同。L／4处的节点位移响应值最大，L／4处的节点位移峰值位于200m左右（L／4处），其响应时程图为反对称，这是由于桥梁的一阶竖向振型为反对称；L／2处的节点位移峰值在410m左右（L／2处），其响应时程图为正对称形状，该节点主要受桥梁竖向第二阶正对称振型的影响。主梁L／4处的速度与加速度响应值均较L／2处节点响应值大。
为了分析车辆速度对主梁L／4和L／2处节点动力响应的影响，现取v＝［0.8v0，v0，1.2v0，1.4v0，1.6v0］，在v的速度下，桥梁关键节点处的动力响应如图7.10所示。不同的行车速度下，主梁节点位移变化趋势相同，但主梁节点位移响应的峰值有所不同。
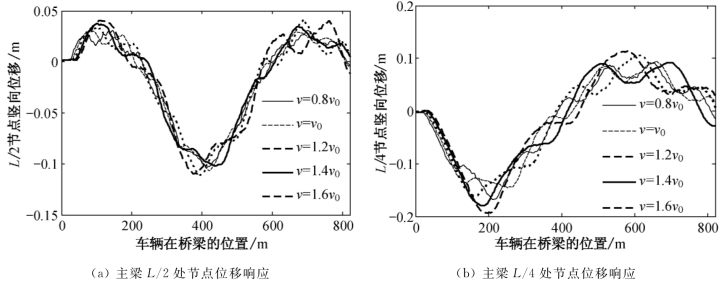
图7.10 不同速度下桥梁L／4和L／2处节点位移响应图
当车速由v＝v0＝72km／h变为v＝0.8v0＝57.6km／h后，主梁L／4处的位移响应值有所增加，而L／2处的位移响应值小幅减小；当车速由v0变化至1.6v0后，主梁L／4处的位移响应值一直增加，而L／2处的位移响应值先增加，速度为1.4v0时，位移响应减小，然后又有所增加。由图7.10（b）可知，速度响应值变化趋势相同，分别在1.2v0和1.6v0处存在极大值，在v0和1.4v0处存在极小值。由此可知，速度对加劲梁动力响应有一定的影响，但不随着速度的变化而单调增加或减小。
上述分析中车辆总重为w0＝5×104kg，为了分析车重对动力响应的影响，分别取车辆重量分别为w＝［0.8，1.0，1.2，1.4，1.6］w0，分析结果如图7.11所示。随着车重的增加，桥梁的位移响应值有所增加。当车重由4×104kg增加到8×104kg时，L／4节点的竖向位移由0.116 9m增加到0.231 3m，L／2节点的竖向位移由0.085m增加到0.173 1m；L／4节点的竖向加速度由0.062 0 m／s2增加到0.124 1 m／s2，L／2节点的竖向加速度由0.040 7m／s2增加到0.080 1m／s2。这表明，车重增加1倍，加劲梁位移响应最大值增加约0.97倍。
本节主要研究了车辆的动力效应、行车速度和车重三个参数对加劲梁位移和加速度响应的影响，可得出以下结论：
（1）静力荷载作用下，加劲梁的响应为平滑的曲线，而考虑车-桥系统耦合振动的动力加载方式作用下，加劲梁的响应具有波动性，且动力响应的最大值大于静力响应。
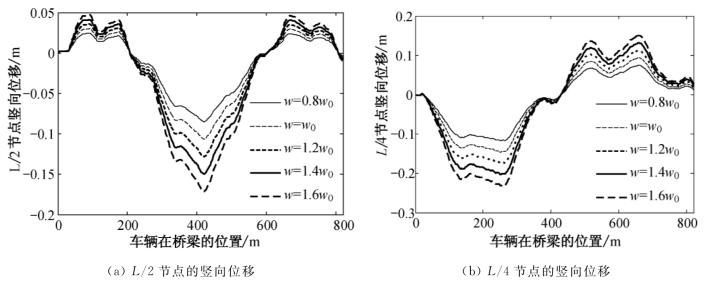
图7.11 不同车重下主梁关键节点的位移响应
（2）速度对加劲梁动力响应有一定的影响，但不随着速度的变化而单调增加或减小。
（3）随着车重的增加，桥梁的位移和加速度响应值均有所增加。车重增加1倍，加劲梁位移响应最大值增加约0.97倍。
相关文章
- 详细阅读
-
桥梁可靠度分析：失效概率与可靠性详细阅读
工程结构可靠度是指在规定的时间内，在规定的条件下，完成预定功能的概率。结构的失效概率是指结构不能完成预定功能的概率，用Pf表示。结构可靠度分析的依据就是根据结构的极限状态计算结构的失效状态的概率。假定式所述两个随机变量的均值和标准差分别为μR、μS和σR、σS，且随机变量均服从正态分布，由此可以获取Z的概率密度函数。......
2025-09-30
-
桥梁可靠度分析方法—综述与应用详细阅读
把结构可靠度引入到工程结构优化设计数学模型中，根据现有的资源及结构功能要求，选取合适的目标可靠指标为约束条件，并采用遗传算法求解，既可以实现此类工程结构优化设计，又能保证结构在使用过程中的安全性。文献［8］建立了半刚性连接框架的拓扑模型，并结合遗传算法进行了基于体系可靠度的结构优化设计，认为不考虑可靠度的优化设计结构存在安全隐患。......
2025-09-30
-
桥梁可靠度分析中的Possion假定详细阅读
定义若r＞3，则无论结构的响应是宽带过程还是窄带过程，Possion假定均能满足精度要求。下面给出考虑密集车辆占有率的Possion假定动力可靠度表达式：由式可计算出界限跨越率和考虑车辆运行状态的大跨度桥梁位移动力可靠度。......
2025-09-30
-
桥梁可靠度分析方法及应用详细阅读
Rocco等［4］提出了联合SVM和MCS求解结构可靠度的方法。SVM在结构体系可靠度分析中的应用较少。为了发展工程结构体系可靠度理论与方法在桥梁安全评估中的应用，本章将建立桥梁结构体系可靠度分析的简化模型，总结现有结构体系可靠度分析方法，提出基于支持向量机的桥梁结构可靠度分析方法，最后采用两个算例分析表明支持向量机在桥梁结构体系可靠度评估中的应用。......
2025-09-30
-
优化结果分析-桥梁可靠度分析方法与应用详细阅读
取目标体系可靠指标β0＝2，截面及荷载变异系数均为ξ＝0.1，遗传算法优化结果如图5.7所示。图5.7遗传算法迭代过程图由图5.7所示桁架结构遗传算法优化过程可以看出，在第40次种群迭代时，适应度值已经稳定并达到收敛，表明优化过程稳定，优化结果可靠。表5.3不同方法优化结果由表5.3所示的不同体系可靠度约束优化结果可以看出，体系可靠性优化后结构的重量较常规优化方法的大。......
2025-09-30
-
桥梁可靠度分析的直接抽样法详细阅读
对于通常的实际工程结构，pf为10-3～10-5数量级，若误差小于20%的置信度为95%，则所需模拟次数N＝105～107。一般抽样法的计算量是相当大的，故适用于模拟精度不高的情况。采用该随机数发生器就避免了循环语句的使用，运行时间更短，效率更高。将所有的随机数都计算完后，把结果存储于矩阵中，然后统计矩阵中Y≥0的数量nf，最后由式计算出失效概率，对应于相应的可靠指标。......
2025-09-30
-
桥梁动力响应概率分析的可靠度方法与应用详细阅读
Chen等［53］的研究结果表明，车流通过桥梁时，车辆与桥梁之间的互相作用力受前后车辆的影响较小，因此可单独提取每个车辆与桥梁的相互作用力的时变力。采用上述EDWL方法可将车辆的每个轴重转换为等效的时变集中力，这样为基于有限元的桥梁动力响应瞬态分析提供了有利条件。图6.17随机车流作用下车-桥耦合振动分析流程动力响应的概率统计分析方面，在ANSYS平台加载随机车流的流程如图6.17所示。......
2025-09-30
相关推荐