桥梁车-桥耦合系统的简化有限元分析方法

2023-09-19 理论教育版权反馈

【摘要】：有限元技术为大跨度桥梁在随机车流作用下的车 -桥耦合振动分析提供了新的思路。基于ANSYS 的车-桥耦合振动分析的关键内容有两个方面，分别是车辆与桥梁模型的建立以及振动方程分离迭代求解方法［49］。下文将对简化模型的分析方法进行描述。车-桥系统的简化运动方程可描述为：式中，下标v为车辆；b为桥梁；u为竖向位移；h为桥梁平整度。

早期的研究中较多采用古典理论的振动微分方程进行分析，这与当时计算技术、计算方法和计算手段的局限性有关。虽然采用Newmark- β方法迭代求解车辆和桥梁运动方程简化了微分方程的计算量，但是针对大跨度桥梁结构而言仍然是费时的。另一方面，针对大跨度桥梁的车 -桥耦合振动响应分析，结构的几何非线性较为显著，加之随机车流样本中车辆数目较多，模态综合方法等不适合大跨度桥梁的车-桥耦合振动响应分析。有限元技术为大跨度桥梁在随机车流作用下的车 -桥耦合振动分析提供了新的思路。计算技术和大型通用有限元软件ANSYS 的出现为车-桥耦合振动求解提供了有利条件。根据ANSYS的APDL语言可分析考虑车辆多参数的多个车辆荷载作用下复杂桥梁的振动响应。基于ANSYS 的车-桥耦合振动分析的关键内容有两个方面，分别是车辆与桥梁模型的建立以及振动方程分离迭代求解方法［49］。

针对车载下大跨度桥梁的动力响应分析，车辆的动力特性对桥梁影响较小，采用弹簧质量模型对振动分析是具有足够精度的［50］。根据ANSYS强大的有限元模拟功能，可以建立简化的车辆模型，车辆模型与桥梁模型在同一模型中，但两个模型相互独立，其耦合关系由APDL语言通过在任意时刻施加于车辆及桥梁的力和位移条件来控制。本书采用平面车辆模型，由ANSYS软件中的Mass 21、Beam 4和Combin 14单元来模拟。其中Mass 21单元模拟车身和车轴的质量，Beam 4单元模拟车辆的纵梁，Combin 14单元模拟车辆的悬挂系统。简化的车辆模型如图6.13～6.14所示。

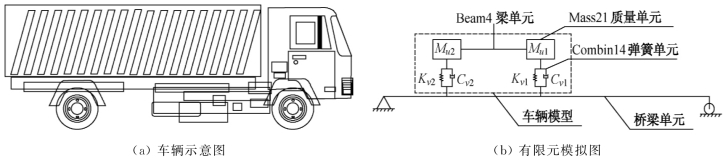
pagenumber_ebook=117,pagenumber_book=107

图6.13　双轴平面车辆（C2）模型

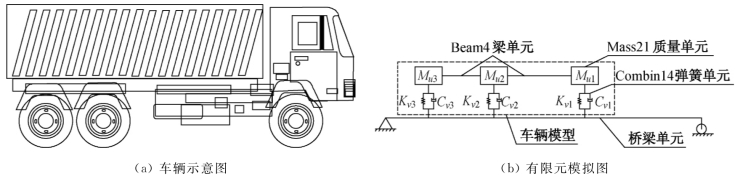
pagenumber_ebook=117,pagenumber_book=107

图6.14　三轴平面车辆（C3）模型

简化车辆模型的每个单元具有三个自由度，分别为纵向、横向和扭转自由度，将车辆动力特性及桥梁平整度对桥梁节点的作用转化为外荷载，从而简化了车桥分析模型。下文将对简化模型的分析方法进行描述。车-桥系统的简化运动方程可描述为：

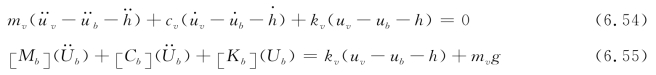
pagenumber_ebook=117,pagenumber_book=107

式中，下标v为车辆；b为桥梁；u为竖向位移；h为桥梁平整度。在一个时间步Δt内h假定是不变的，可改写为：

车与桥面的相对竖向位移d＝uv-ub，则式（6.56）可改写为：

式（6.57）的边界条件为di（ts）＝di-1（te），d（0）＝d（∞）＝0，其中di（ts）表示第i个时间开始时车辆与桥梁的相对位移，di-1（te）表示第（i-1）个时间末车辆与桥梁的相对位移。由式（6.57）可得到任意时刻车辆-桥梁的相对位移：

di（te）＝h+c1ec2Δt　（6.58）

c1＝di-1（te）-h　（6.59）

pagenumber_ebook=117,pagenumber_book=107

d0（te）＝d（0）＝0　（6.61）

通过对第i个时间步的振动分析，可得出桥梁的节点位移ub，代入式可得车辆的振动位移uv，至此，车辆的增量方程可表示为：

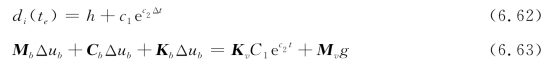
pagenumber_ebook=118,pagenumber_book=108

在ANSYS中提取质量矩阵和刚度矩阵的方法较为简单，而在阻尼矩阵的定义方面较为复杂。结构阻尼大小与周围介质的黏性、结构本身的黏性以及地基的参量耗散等方面的因素有关。通常结构分析中的阻尼为瑞利阻尼，其表达式为：

式中，α为质量阻尼系数，β为刚度阻尼系数，其数值可通过振动阻尼比得出：

pagenumber_ebook=118,pagenumber_book=108

式中，ωi和ωj分别表示桥梁的第i阶和第j阶频率；ξi和ξj分别表示第i阶和第j阶振型的阻尼比。阻尼比可由荷载试验确定，大量的试验数据［51］表明，预应力混凝土结构桥梁的阻尼比在0.05左右，本书的分析中均取ξ＝0.05，然后计算阻尼矩阵。

ANSYS 可分析结构瞬态行为中的非线性-大变形、接触和弹塑性分析等［52］。ANSYS的瞬态分析求解方法如图6.15所示。

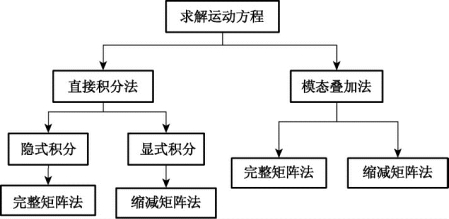
pagenumber_ebook=118,pagenumber_book=108

图6.15　ANSYS瞬态分析的求解方法

图6.15中，采用直接积分方法时，运动方程可以直接对时间按步积分，在每个时间点，需要求解一组联立的静态平衡方程。其中，直接积分方法为Newmark-β方法。求解时可采用缩减结构矩阵，也可用完整的结构矩阵。缩减矩阵可快速求解，但缩减后的质量和阻尼矩阵是近似的，会使结果产生一定的误差。积分时间步长（ITS）的选取是ANSYS进行瞬态分析的关键内容，应小于结构一阶振型周期和荷载突变时间。

在进行车-桥系统运动求解时，有几个假定，首先车辆过桥时车轮与桥面始终保持接触，也就是车辆与桥梁的位移相同，根据车轮与桥面接触点的力与位移协调条件，可得到车辆对桥梁的动力荷载：

式中，i＝1，2，…，N，其中N为车辆的轴数；Fbi为第i个车轴对桥梁产生的动力荷载；Cti和kti分别为第i个车轴的阻尼系数和等效刚度；δti（s，t）为t时刻第i个车轮接触点处桥梁的竖向位移；r（si）为某时刻第i个车轴轮处的桥面平整度。根据车辆的运动方程和车辆与桥梁之间的接触条件，可导出车辆系统的外部激励fvi的表达式为：

本书采用Newmark-β方法求解车辆和桥梁的运动微分方程，两者之间通过车轮与桥梁连接位置的几何相容方程和相互作用力的协调条件建立运动方程，采用迭代方法满足两者之间的位移和力平衡条件。ANSYS有限元的利用，避免了每个时间步都重新计算对应时刻的系统质量矩阵、阻尼矩阵和刚度矩阵，提高了运算效率。该简化方法的分析流程如图6.16所示。其中，基于ANSYS 的车-桥耦合振动分析的主要步骤为：

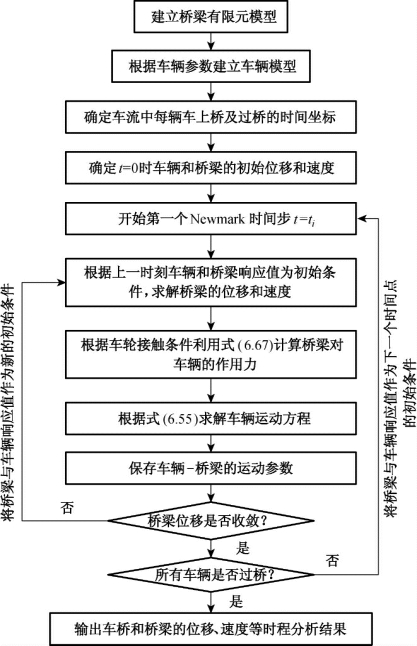
pagenumber_ebook=119,pagenumber_book=109