车桥耦合振动理论与分析方法《桥梁可靠度分析方法与应用》提取

2023-09-19 理论教育版权反馈

【摘要】：由于发动机的振动和路面平整度等原因使得了车-桥系统耦合振动现象更加显著。我国规范中以冲击系数的方式考虑车 -桥耦合振动响应，在实质上该方法是静力分析范畴，不能反映出实际车辆荷载作用下结构的真实响应。图6.11空间车辆模型在车-桥系统的动力响应求解方面主要采用将车辆与桥梁划分为两个子系统，分别建立各自的运动方程，然后建立位移协调和力学平衡条件的方法求解。

车辆以一定的速度在桥面行驶会使桥梁产生随时间变化的位移，同样车辆也会随之上下运动，车辆的振动使得桥梁振动加剧，这样就形成了车桥与桥梁系统的耦合振动。由于发动机的振动和路面平整度等原因使得了车-桥系统耦合振动现象更加显著。我国规范中以冲击系数的方式考虑车 -桥耦合振动响应，在实质上该方法是静力分析范畴，不能反映出实际车辆荷载作用下结构的真实响应。随着各国交通和土建事业的迅速发展，车辆速度和载重都有所提高，车桥耦合振动研究工作更加突出。大跨度桥梁的车-桥耦合振动响应研究也是国内外学术界与工程界领域的热点研究内容。

车辆行驶过程中对桥梁的影响与时间因素密切相关，因此大多学者选择时域分析法来进行车 -桥耦合的研究。目前主要研究方法有整体法和分离法两种，整体法将车辆和桥梁结合为整体并建立整体的运动方程求解，而分离法则是分别建立车辆和桥梁的运动方程，再根据力学平衡和位移平衡条件联立方程求解。整体法在早期的研究中应用较多，但随着车辆模型的复杂化以及耦合自由度的多样化，该方法的计算量较大，求解困难。分离法解决了整体法大量复杂时变系数矩阵求解的问题，通过分离建立运动方程、协调函数和迭代求解方法计算车辆和桥梁的响应，大大降低了计算量，目前得到了广泛的应用。本小节主要从车辆模型、车辆和桥梁的振动微分方程和Newmark β迭代方法等3个方面阐述分离迭代方法在车-桥系统响应分析中的应用。

1）车辆模型

如图6.11所示为空间车辆的模型简图，假定车身与车轴为刚体，用深色表示，两者通过假设弹簧阻尼进行联系。湖南大学的殷新锋［41，42］将车体划分有三个自由度，分别为竖向移动yt、侧翻转动φt和俯仰转动θt，车辆前后轴共模拟了竖向移动和翻滚转动四个自由度，分别用表示，完整的空间车辆模型共有七个自由度。

2）车-桥振动微分方程

针对大跨度桥梁而言，车-桥系统的耦合响应受桥梁的位移影响较大，车辆的耦合力主要受桥梁变形而产生的位移激励影响，车辆的动力响应又放大了桥梁的位移响应［43］。因此，位移协调条件和力学平衡是分离迭代方法中求解车辆和桥梁响应的基础。位移协调采用了车辆的轮轴与桥梁面板始终保持接触的假定，结合桥面的平整度参数使车辆和桥梁的位移相互转换。力学平衡条件采用了每个时刻车辆对桥梁的作用力与桥梁对车辆的反作用力均相等的基本假定。

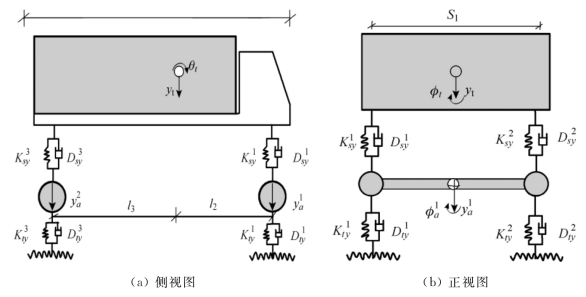
pagenumber_ebook=114,pagenumber_book=104

图6.11　空间车辆模型

在车-桥系统的动力响应求解方面主要采用将车辆与桥梁划分为两个子系统，分别建立各自的运动方程，然后建立位移协调和力学平衡条件的方法求解。由此建立的车-桥耦合运动方程［44］为：

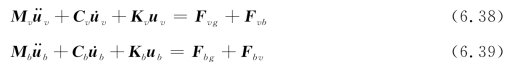
pagenumber_ebook=114,pagenumber_book=104

式中，Mv和Mb分别表示车辆和桥梁的质量矩阵；Cv和Cb分别表示车辆和桥梁结的阻尼矩阵；Kv和Kb分别表示车辆和桥梁的刚度矩阵；uv和ub分别表示车辆和桥梁的位移列向量；Fvb和Fbv 分别表示车 -桥耦合振动时车辆和车辆与桥梁的相互作用力；Fvg和Fbg分别表示作用在车辆和桥梁上与车- 桥耦合不相关的荷载列向量。

3）Newmark-β逐步积分方法

车辆通过桥梁时，车辆的位置一直发生变化，车-桥耦合振动方程矩阵具有时变性。难以直接用数值方法求解微分方程的精确解，目前主要采用逐步积分方法。以较小的时间步长Δt来对结构进行反应求解，在时间步长的开端和结束端分别建立相应的动力平衡条件，忽略中间的不平衡情况。目前主要有Newmark- β、线性加速度法和Wilson θ法三种逐步积分方法［45］，其中，线性加速度法计算精度最高，Wilson-θ法的计算精度最低，本书选取了综合效果较好的Newmark-β法。在（t+Δt）时刻，系统的运动方程为：

式中，时段的步长为Δt，在t和（t+Δt）时刻，系统对应的加速度分别为根据Newmark-β逐步积分方法可知，在t到（t+Δt）时段内的任一时刻（t+ι），系统对应的加速度、速度和位移应该满足以下关系［46］：

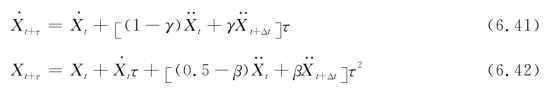
pagenumber_ebook=114,pagenumber_book=104

式中，β和γ需根据积分精度以及稳定性来确定。在目前的研究中，通常对上述参数按照以下要求进行取值，β＝0.25和γ＝0.5，这对该方法的稳定性和精确度方面有了保障。于是可得：

pagenumber_ebook=115,pagenumber_book=105

若将与t和（t+Δt）之间的加速度增量表示，即则有：

pagenumber_ebook=115,pagenumber_book=105

当时间由t变化到（t+Δt）时，可得出在Δt时间内的系统运动方程为：

由此可得出：

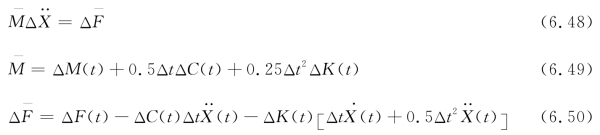
pagenumber_ebook=115,pagenumber_book=105

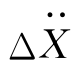式中，分别为体系相应的等效质量以及等效荷载增量。在每个时间迭代点中，该质量和等效荷载均采用上一步计算的结果，这样，二阶微分方程就转换成了普通矩阵方程。由此求解加速度的增量 pagenumber_ebook=115,pagenumber_book=105 ，速度和位移增量由式（6.51）～式（6.52）计算：

Xt+Δt＝Xt+ΔXt　（6.52）

再通过可以得出以此重复计算解出（t+nΔt）时刻对应的位移、速度和加速度。

4）路面平整度

路面平整度的激励（IRR）是车-桥耦合振动系统的主要激励之一，建立合适的路面平整度模型是车-桥耦合振动系统的关键步骤之一。目前路面平整度模型主要有频域模型和时域模型。频域模型可参考文献［47］，由于本书采用响应的时程分析，因此路面平整度模型采用了时域分析方法。

针对路面平整度的时域模型，国内外学者提出了诸多种模拟方法，目前主要有三角级数法、AR方法和Possion方法等。根据三角级数方法［48］，路面平整度函数为：

pagenumber_ebook=115,pagenumber_book=105

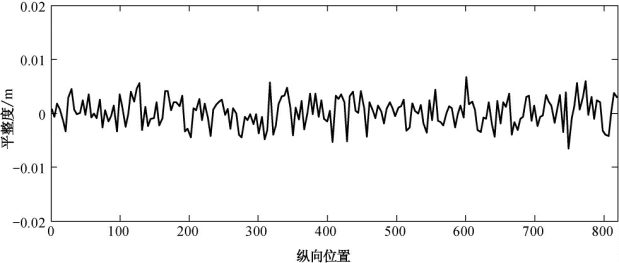
式中 pagenumber_ebook=116,pagenumber_book=106 其中：n为空间频率，n0＝0.1（1／m）是标准空间频率，Gq（n0）为路面平整度系数；θi为0～2π的均匀分布随机数。针对刚通过的桥梁路面情况，路面等级为“很好”，路面平整度系数的下限为8mm3／辆，上限为32mm3／辆，均值为16mm3／辆，由此得出的路面平整度如图6.12所示。

pagenumber_ebook=116,pagenumber_book=106

图6.12　路面平整度样本

本小节对车 -桥系统的分析模型与方法进行了总结，建立了7自由度双轴车辆的空间模型，阐述了车-桥系统的分析理论，介绍了求解车-桥振动微分方程的Newmark-β逐步积分方法，最后建立了路面平整度的时域模型。

车桥耦合振动理论与分析方法《桥梁可靠度分析方法与应用》提取

相关推荐