20世纪70年代初期，河海大学等单位将随机模拟技术应用于水文研究，取得了丰硕成果。......
2023-08-23
随机车流模拟方法与应用
【摘要】：本书在MATLAB语言平台编制五参数的随机车流模拟程序，该程序界面如图6.8所示。图6.8基于MATLAB语言的随机车流模拟软件图6.9随机车流模拟流程图在随机车流模拟软件的基础上，可方便快捷地实现随机车流模拟。图6.10随机车流统计数据与随机样本图车辆的日通行数量具有一定的波动性，但随着运营时间的增长总体呈上涨趋势。与多项式函数相比，指数函数与对数函数对预测车流模型有较好的效果。
在得出车辆参数的分布类型与概率分布特征之后，即可按照各自的概率密度函数进行抽样得出随机车辆样本，连续抽样形成随机车流样本。王达等［34］在MATLAB语言平台编制了单一车辆随机车流模型（STVFM）和混合车型随机车流模型（ATVFM）的软件。韩万水课题组成员［35，36］开发了RTF（随机车流）软件来模拟四参数（车型、车速、车距和车重）条件下的随机车流模拟软件。
本书在MATLAB语言平台编制五参数（车型、车道、车速、车重和车距）的随机车流模拟程序，该程序界面如图6.8所示。在时域内生成随机车流的步骤如图6.9所示。
图6.8 基于MATLAB语言的随机车流模拟软件
图6.9 随机车流模拟流程图
在随机车流模拟软件的基础上，可方便快捷地实现随机车流模拟。同时，也可以多次抽样，对抽样结果进行可信检验和筛选。基于上述WIM系统的车流量参数统计与随机车流模拟软件可对宜泸高速公路南溪长江大桥的车流量进行模拟，并生成不同运行状态下的随机车流样本，如图6.10所示。
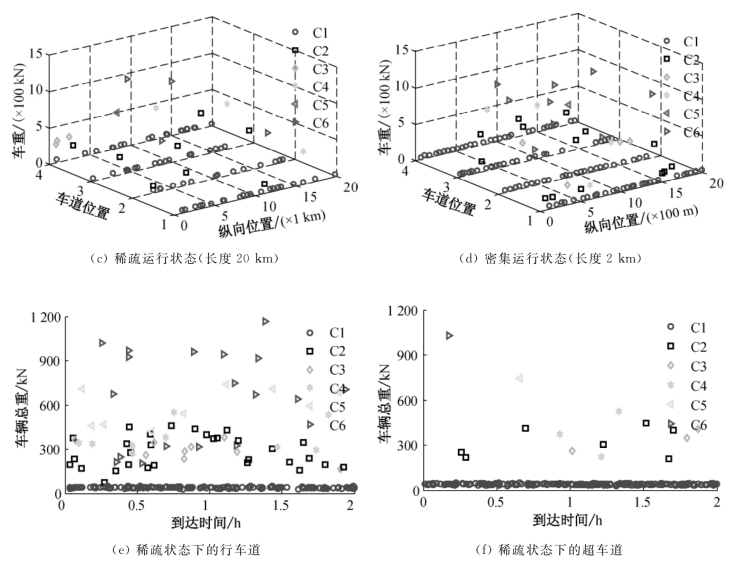
图6.10 随机车流统计数据与随机样本图
车辆的日通行数量具有一定的波动性，但随着运营时间的增长总体呈上涨趋势。根据现有的统计数据，采用多项式函数、指数函数和对数函数拟合并预测交通量数据，其表达式分别为：
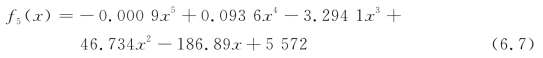
f6（x）＝5 566exp（0.002 2x） （6.8）
f7（x）＝477.18ln x+5 166 （6.9）
式中，x为桥梁以10天为单位的服役时间。
与多项式函数相比，指数函数与对数函数对预测车流模型有较好的效果。然而，指数函数预测的车流量呈加速增加趋势，不符合实际车辆情况；对数函数的增长系数呈减速增长趋势，与实际交通量的增长情况较为吻合。由此预测出20年后的交通量为8 153辆，平均年线性增长系数为2.84%。
有关桥梁可靠度分析方法与应用的文章
- 详细阅读
-
随机模拟：模拟事件出现及服务时间的随机概率详细阅读
将随机数作为事件出现的随机概率进行模拟工作步骤①求出模拟事件出现的概率。④从随机数表中任意指定一个随机数作为始点，一个一个的模拟。由于表7-5中分布概率、累计频率和随机概率只精确到小数点后两位数，所以获取的随机数只需两位数即可。表7-7 随机数与相应的服务时间3）将随机数加以改造，作为实际发生的事件进行模拟。目的是使模拟随机数的平均数与均方差和模拟事件的平均数与均方差相等。......
2023-07-15
-
月径流量随机模拟方法及效果详细阅读
月径流资料的模拟生成。8.2.2.3月径流模型的验证和分析将上述马尔柯夫过程模型、分解计算法和解集模型3种方法的模拟结果作对比以判断其优劣。......
2023-08-23
-
随机车流对桥梁的影响详细阅读
图7.1212min内加劲梁的竖向位移时程图表7.8随机车流作用下悬索桥动力响应值汇总表（续表）由图7.12所示随机车流作用下悬索桥的动力响应分析结果表明，悬索桥加劲梁不同位置处的响应不同，车辆的运行状态对加劲梁的动力响应影响较大。按照公路-Ⅰ级车道荷载加载至加劲梁的影响线，可得到规范所得的位移值。......
2023-09-19
-
桥梁可靠度分析方法与应用：随机变量与随机过程详细阅读
描述工程结构中不确定性的基本方法就是随机变量与随机过程。随机变量的概率分析是描述随机变量概率特征的重要依据。简而言之，随机过程就是依赖于时间t的一主随机变量，则X称为随机过程在t1时刻的随机变量［15］。图1.2随机过程样本与均值的关系随机过程的方差D表示随机过程在t时刻对于均值点的偏离程度。仅对于正态随机过程而言，两者一致，工程中常用的是平稳随机过程。......
2023-09-19
-
桥梁可靠度分析方法：基于随机车流的首超概率模详细阅读
研究重载车辆作用下大跨度桥梁的随机振动响应，据此可以分析在役大跨度桥梁的动力可靠度，可从概率角度评估桥梁的安全性和适用性，也可为桥梁的运营管理决策提供理论依据。采用重载车流模型加载至桥梁结构进行随机振动分析，能够更加真实地模拟车辆通过桥梁的动力行为，随机车流和随机路面激励可捕捉桥梁响应的概率特征，且可通过改变车辆轴重和车辆密度模拟交通量变化，用以预测桥梁生命周期内交通荷载对结构可靠性的影响。......
2023-09-19
-
桥梁可靠度分析方法与应用中的随机过程特征详细阅读
图7.13随机车流作用下加劲梁位移响应均值由图7.13可知，在随机车流作用下加劲梁位移响应均值趋于收敛，因此，其位移响应为平稳随机过程。上述分析证明了结构响应为平稳随机过程并且具有各态历经性。表7.9随机车流作用下结构响应的均方根值图7.16随机车流作用下加劲梁的位移功率谱密度采用同样的方法求得响应均方根沿全桥加劲梁纵向分布情况如图7.17所示。......
2023-09-19
-
南溪长江大桥在随机车流下的疲劳应力分析详细阅读
表8.15C2车型的轴重均匀设计表单位：kN通过20次有限元计算和雨流计数提取应力循环，并转换为等效应力幅值Seq，通过SVR回归分析可得到C2车型的轴重与Seq的SVR模型。将该车辆样本代入C2车型的SVR模型中可得到各车辆样本对应的钢箱梁细节处的等效应力幅Seq。表8.16某日随机车流作用下细节①的疲劳应力计算结果备注：各车型车辆的数量为全桥单向行驶的数量，即仅考虑半幅通车数量。......
2023-09-19
相关推荐