基于WIM的车辆统计分析

2023-09-19 理论教育版权反馈

【摘要】：图6.2某高速公路的WIM系统现场照片1）车型该高速公路WIM系统在2013年3月1日至7月31日，共计153天，采集到约107万辆车辆数据。表6.16种典型车辆的车型参数表6.2某高速公路车型占有率图6.3车型占有率的饼形统计图2）车速车辆行驶速度与众多因素有关，主要有车型、驾驶员行为、环境因素和交通情况等，因此行车速度需要由概率统计得出。图6.6W62轴重概率密度分布图6.7密集运行状态下车距概

动态称重（Weigh In Motion，WIM）系统是安装在路面面层以下的一套传感器系统，用以获取通过车辆的轴重、车速和车型等参数。随着传感器技术的迅速发展，目前的WIM系统具有较高的控制精度，通过WIM系统的大量统计数据可建立车辆的概率模型。本节采用了四川省某高速公路的WIM系统及其车辆统计数据，该系统的现场施工照片如图6.2所示。

pagenumber_ebook=99,pagenumber_book=89

图6.2　某高速公路的WIM系统现场照片

1）车型

该高速公路WIM系统在2013年3月1日至7月31日，共计153天，采集到约107万辆车辆数据。根据车辆的轮轴配置，将所有车辆划分为C1～C6等6种类型，然后统计每种车型的参数概率特征。C1车型表示小型客车，C2～C6车型表示2～6轴货车。C1～C6的车型参数如表6.1所示，每种车型的占有率如表6.2和图6.3所示。

表6.1　6种典型车辆的车型参数

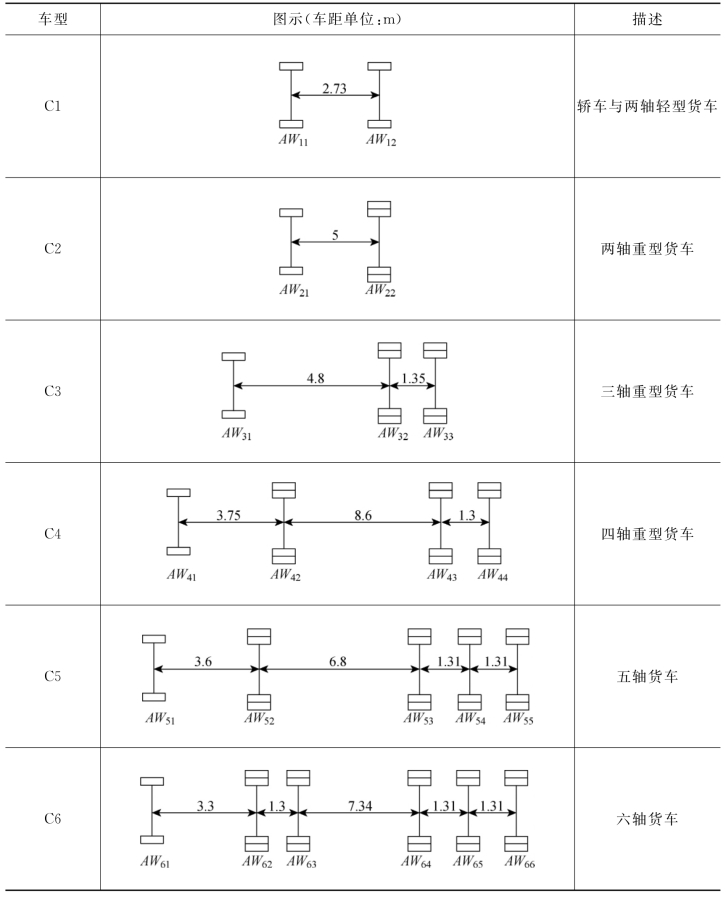
pagenumber_ebook=100,pagenumber_book=90

表6.2　某高速公路车型占有率

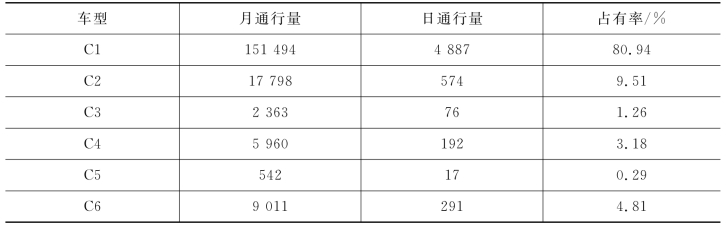
pagenumber_ebook=101,pagenumber_book=91

图6.3　车型占有率的饼形统计图

2）车速

车辆行驶速度与众多因素有关，主要有车型、驾驶员行为、环境因素和交通情况等，因此行车速度需要由概率统计得出。王达［10］和韩万水［12］的研究结果表明，车速一般服从正态分布。根据南溪长江大桥的WIM系统采用数据，按6种车型分类后的车速统计与拟合效果如图6.4所示，相关参数如表6.3所示。

pagenumber_ebook=101,pagenumber_book=91

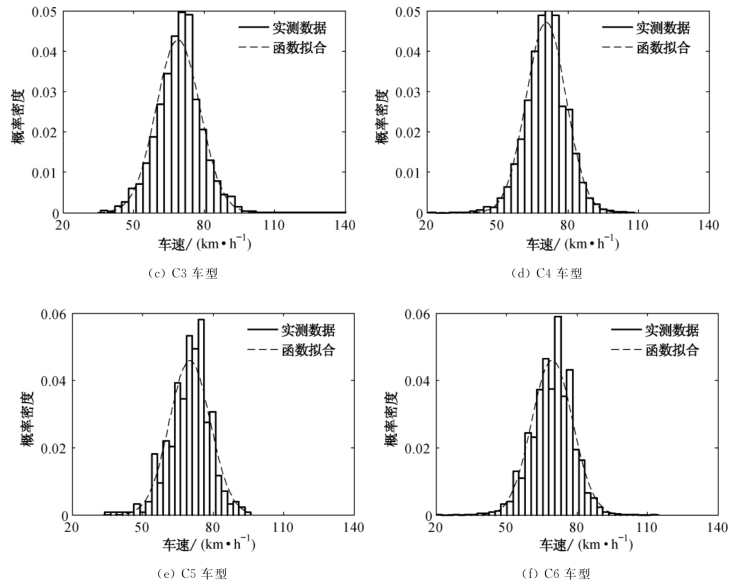
pagenumber_ebook=102,pagenumber_book=92

图6.4　C1～C6车型的车速概率分布与拟合图

表6.3　C1～C6车型的车速概率分布拟合参数

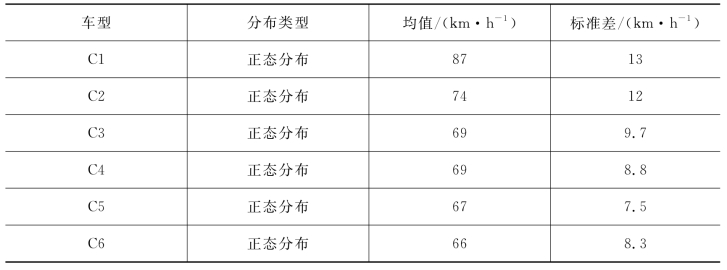
pagenumber_ebook=102,pagenumber_book=92

由图6.4和表6.3可知，各车型的实测速度值与正态分布函数的拟合值较为接近，C1车型的车速均值和标准差均较其他车型的大，C6车型的车速均值最小。

3）车重

郭彤等［27］对公路桥梁车辆轴重的统计研究以及吕磊等［28］对某大跨度悬索桥的实测轴重数据的研究结果均表明，高速公路车辆荷载呈现多峰分布特点，而常规的正态分布和非正态分布具有单峰分布特征，无法准确拟合车辆荷载的总重和轴重。

高斯混合模型（GMM）［29］是在高斯模型（GM）的基础上进行延伸和扩展得到的一种由多种高斯函数按照一定比例组合成面的混合模型。理论上，GMM可以采用有限GM模型组合起来拟合任意形状的概率密度分布。GMM是一种模拟统计规律的有力工具，已经在视频背景更新、数据聚类和语音识别等领域有着较广泛的应用，而在交通量的统计分析领域应用较少。徐程［30］采用高斯混合模型对车流量的速度分布进行了拟合，分别得出了一般运行状态和密集运行状态下车辆的速度概率密度函数。梅刚［31］采用极值Ⅰ型和正态分布函数的混合模型对京沪高速公路车辆的轴重进行拟合，将重型车辆分为空载、一般和重载三种情况，最后以轴重最大值分布的0.95分位值作为桥梁在剩余可靠度研究中的评估荷载。

针对某一类车型，按照其实际载重量大小可以分为空载、一般载重和超载3种情况，这就需要3个高斯模型来拟合这3种车重分布，将这3种高斯模型按照一定比例结合就形成了拟合原车重分布的高斯混合模型。根据上述原理，车重的GMM模型可表示为：

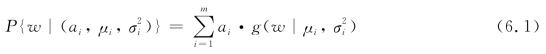
pagenumber_ebook=103,pagenumber_book=93

式中，m表示高斯混合模型中正态分布的数量；w为车重；ai为高斯混合分布的权重，也表示为该类车型所占比例，ai应满足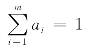 pagenumber_ebook=103,pagenumber_book=93 的条件；g（·）为基准高斯分布密度函数，见式（6.2）：

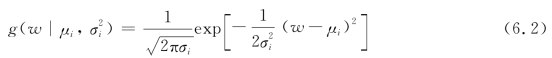
pagenumber_ebook=103,pagenumber_book=93

式中，μi为第i个高斯分布函数的均值；σi为第i个高斯分布函数的标准差。由于高斯混合模型中存在诸多变量，选择不同的模型结构会得到不同的混合模型。其中，权重系数ai的选择是高斯混合模型的核心，它表示了车辆样本中，各类车辆所占比例。

在高斯混合模型的结构确定之后，需要对模型中的参数（ai，σi，μi）进行优化求解。McLachlan等［33］采用了多种方法对其参数进行估计，研究结果表明期望最大化（EM）算法具有较好的适用性。EM算法是极大似然估计方法中的一种，可以分为E步骤（求期望）和M步骤（期望最大化），通过两个步骤的不断迭代优化求解。该算法对于求解隐形变量和数据缺失问题具有较好的效果。GMM模型的似然函数表示为：

pagenumber_ebook=103,pagenumber_book=93

式中，初始参数为Θ＝（wi，μi，σi），其参数无法采用求导方法取得最大值，本书采用了EM优化算法分步迭代求解最大值对应的各个参数值。具体步骤为：

（1）初始化参数Θ＝（wi，μi，σi）。采用K-means算法对样本数据点进行聚类，根据聚类结果选取参数数量及其对应的数值。

（2）E步骤。估算车重样本数据中每个高斯函数所占的比例，对于某个车重样本值wk，它由第i个高斯函数组合的概率为：

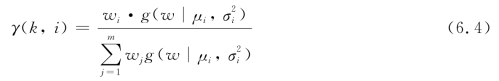
pagenumber_ebook=104,pagenumber_book=94

（3）M步骤。对式（6.4）进行求导，得出似然函数对应的参数估计值：

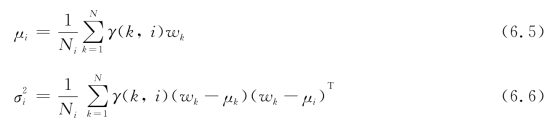
pagenumber_ebook=104,pagenumber_book=94

式中， pagenumber_ebook=104,pagenumber_book=94 由于因此在GMM似然函数中引入拉格朗日乘子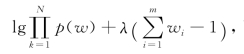：可求得该函数取得最大值时ai对应的数值为。

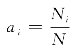（4）计算似然函数值并检查其是否收敛，若不收敛，则迭代E和M步骤；若收敛，则参数对应的值即为各参数的最大似然估计值。

根据南溪长江大桥WIM监测系统2014年3月的车辆总重数据，采用GMM方法对各车型的总重进行拟合，实测数据的统计与GMM拟合图如图6.5所示。

pagenumber_ebook=104,pagenumber_book=94

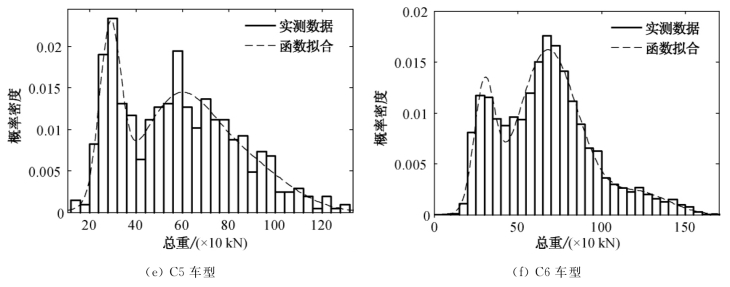
pagenumber_ebook=105,pagenumber_book=95

图6.5　C1～C6车型的总重统计与拟合图

由图6.5可知，宜泸高速公路南溪长江大桥车辆轴重具有显著的多峰分布特点，采用多参数的高斯混合模型可对车辆的轴重数据进行准确的拟合。

4）车距

统计结果表明车型服从均匀分布，车速服从正态分布，车重概率密度函数具有多峰特征，车距具有显著的时变性。根据统计数据，采用高斯混合模型（GMM）拟合了每种车型的每个轴重。在此，以C6车型的第2个轴重（W62）为例，给出其概率密度函数，如图6.6所示。

车距的概率分布随着时间变化较大，且车距分布直接影响大跨度桥梁的动力响应。本书根据车距特征将车辆运行状态划分为3种：稀疏状态、一般状态和密集状态，目前针对这3种状态并无明确的界限划分，宗周红［32］建议以2s的时距划分车辆的密集与稀疏状态。本书采用以下划分准则：稀疏状态的车距大于500 m，一般状态的车距大于100 m小于500m，密集状态的车距小于100m。密集状态车辆车距的概率密度函数可采用Gamma函数进行拟合，如图6.7所示。其中，Gamma函数的k与θ值分别为6.43与9.15。

pagenumber_ebook=105,pagenumber_book=95

图6.6　W62轴重概率密度分布

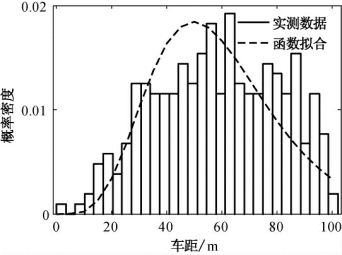
pagenumber_ebook=105,pagenumber_book=95

图6.7　密集运行状态下车距概率分布

车速的概率特征与车型及车辆的密集状态有关。统计数据表明，稀疏运行状态下，C1车型车速服从均值为87km／h，标准差为13km／h的正态分布；C6车型车速服从均值为66km／h，标准差为8.3km／h的正态分布。密集运行状态下，每种车型的车速均服从均值为52km／h，标准差为4.3km／h的正态分布。由于车速具有时变性，该概率模型仅用于生成车辆的初始车速。

基于WIM的车辆统计分析

相关推荐