针对中心点法计算精度较低的问题，Hasofer和Lind等提出了验算点法［2］。图2.1当量正态化示意图图2.2n维空间的极限状态曲面图假设受n个非正态分布随机变量影响的结构极限状态方程为：Z＝g（X1，X2，…由公式（2.3）、和联立可求解可靠指标β和验算点。值得注意的是，在由Newton迭代法求出β值后，按式计算原坐标系中的验算点时，应区分正态分布和非态分布参数的μXi值。......
2025-09-30
桥梁可靠性分析方法与应用
【摘要】：由设计结构的内力分析可知，H1和H7的内力较小，可忽略其失效特性。表5.4钢桁梁结构静力计算结果选取纵梁、横梁弯曲失效E1，受压腹杆屈曲失效E2和受拉腹杆拉应力失效E3这3种失效模式。由图5.12可以看出，设计结构的最初失效状态表现为H3和H6杆件的屈曲失效，最终失效状态表现为L1和L2杆件弯曲失效后在跨中位置形成塑性铰，而出现不适宜加载的过大变形。图5.12钢桁梁结构失效树
采用通用有限元软件ANSYS建立了3个标准梁段的简化有限元模型（如图5.10所示）。上弦杆、下弦杆、上横梁和下横梁均为BEAM189梁单元，斜腹杆和竖腹杆为LINK8杆单元，在吊索位置施加简支约束。各杆件编号和失效位置如图5.11所示。
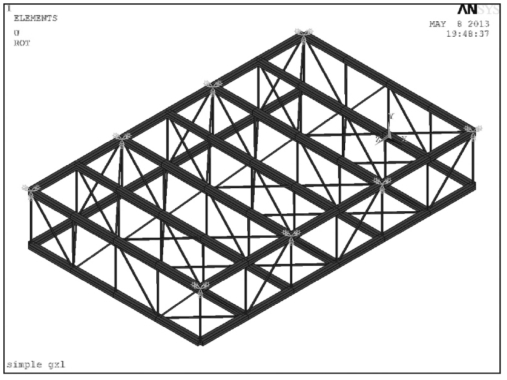
图5.10 3个标准梁段的钢桁梁有限元模型
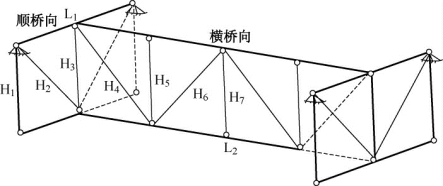
图5.11 杆件编号和失效位置图
荷载工况为：自重+集中力。其中，集中力按车辆重力标准值取550kN［20］，数量为4个，横向间距为3.375m。集中力按影响线加载，按图5.11所示位置取以下3个工况：
工况1：考虑压杆H2、拉杆H4和横梁L1的失效，集中力加载位置为1、2、3和4号点。
工况2：考虑压杆H6的失效，集中力加载位置为图5.9（b）中的3、4、5和6号点。
工况3：考虑横梁L2的失效，加载位置为3、4和5号点。
由设计结构的内力分析可知，H1和H7的内力较小，可忽略其失效特性。H2和H4同为拉应力且荷载布置相同，取拉应力较大的H4杆件为代表。H3和H5同为压应力且荷载布置相同，取压应力较大的H4杆件为代表。按照以上3个荷载工况与自重作用效应，钢桁梁的静力计算结果如表5.4所示。(https://www.chuimin.cn)
表5.4 钢桁梁结构静力计算结果
选取纵梁、横梁弯曲失效E1，受压腹杆屈曲失效E2和受拉腹杆拉应力失效E3这3种失效模式。功能函数如式（5.14）所示，其中i＝2，j＝2，k＝1，即弯曲失效杆件为L1和L2，屈曲失效杆件为H3和H6，拉应力失效杆件为H4。
选取横梁截面高度h1、宽度w1、腹杆截面高度h2和集中力F为随机变量。其中h1，w1和h2服从正态分布，均值为设计变量值，变异系数ξ1＝0.05；F服从极值Ⅰ型分布，均值为550kN，变异系数为ξ2＝0.08。
考虑钢桁梁的失效历程，当纵梁和横梁发生弯曲失效时，在失效位置增加塑性铰；当腹杆发生屈曲失效或拉应力失效时，删除该失效单元。在每次失效状态出现后，重新构建神经网络，继续加载分析，直至结构为变机动结构或出现过大变形。由此构建的失效树如图5.12所示。
由图5.12可以看出，设计结构的最初失效状态表现为H3和H6杆件的屈曲失效，最终失效状态表现为L1和L2杆件弯曲失效后在跨中位置形成塑性铰，而出现不适宜加载的过大变形。其中L1出现塑性铰后位移为11.2cm，L2出现塑性铰后位移为12.4cm。采用RBFMC方法可得出该结构的体系可靠指标βs＝5.49。
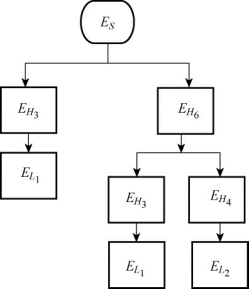
图5.12 钢桁梁结构失效树
相关文章
- 详细阅读
-
桥梁抽样方法分析-桥梁可靠度分析方法与应用详细阅读
一般的MC法用于高度非线性的极限状态曲面或者随机变量维数较高的情况，使用在笛卡儿坐标下的抽样模拟法效率较低，计算耗时较多。因此，Ditlevsen、Olesen、Mohr提出了在标准正态空间中极坐标下进行抽样的方向抽样MC法。③重复步骤①和②直到N次，利用式估计失效概率。对于极限状态曲面接近球面的情况，方向抽样MC法比笛卡尔坐标空间的MC法占较大的优势，若计算接近平面的极限状态曲面时，则无优势。......
2025-09-30
-
桥梁可靠度分析方法—综述与应用详细阅读
把结构可靠度引入到工程结构优化设计数学模型中，根据现有的资源及结构功能要求，选取合适的目标可靠指标为约束条件，并采用遗传算法求解，既可以实现此类工程结构优化设计，又能保证结构在使用过程中的安全性。文献［8］建立了半刚性连接框架的拓扑模型，并结合遗传算法进行了基于体系可靠度的结构优化设计，认为不考虑可靠度的优化设计结构存在安全隐患。......
2025-09-30
-
桥梁可靠度分析方法及应用详细阅读
Rocco等［4］提出了联合SVM和MCS求解结构可靠度的方法。SVM在结构体系可靠度分析中的应用较少。为了发展工程结构体系可靠度理论与方法在桥梁安全评估中的应用，本章将建立桥梁结构体系可靠度分析的简化模型，总结现有结构体系可靠度分析方法，提出基于支持向量机的桥梁结构可靠度分析方法，最后采用两个算例分析表明支持向量机在桥梁结构体系可靠度评估中的应用。......
2025-09-30
-
桥梁可靠度分析方法与应用-算例分析结果详细阅读
表2.1计算结果比较图2.4算例1迭代过程图2.5算例2迭代过程图中虚线为采用文献［10］的响应面法的迭代过程，实线为改进后的响应面法迭代过程。计算结果表明：算例1的一次二阶矩法结果与文献［13］同种方法给出的结果β＝2.3309，几乎相等；而算例2的一次二阶矩法计算结果不收敛无法得出结果。......
2025-09-30
-
桥梁可靠度分析方法与应用：随机变量与随机过程详细阅读
描述工程结构中不确定性的基本方法就是随机变量与随机过程。随机变量的概率分析是描述随机变量概率特征的重要依据。简而言之，随机过程就是依赖于时间t的一主随机变量，则X称为随机过程在t1时刻的随机变量［15］。图1.2随机过程样本与均值的关系随机过程的方差D表示随机过程在t时刻对于均值点的偏离程度。仅对于正态随机过程而言，两者一致，工程中常用的是平稳随机过程。......
2025-09-30
-
桥梁可靠度分析方法应用：支持向量回归详细阅读
支持向量机是由Vapnik［7］提出的一种机器学习方法，主要有支持向量分类和支持向量回归两种算法。由于SVR是目前结构可靠度分析中的一种较为新颖的方法，下文将简单介绍SVR在结构响应函数拟合应用中的相关理论。SVR学习理论主要是通过如式（3.2）所示的ε敏感函数［8］来控制SVR模型的拟合误差。由式（3.5）可得到SVR模型的函数表达式：为了提高建立SVR模型的效率与精度，可通过对输入样本点及SVR模型参数进行优化。......
2025-09-30
-
桥梁可靠度分析：失效概率与可靠性详细阅读
工程结构可靠度是指在规定的时间内，在规定的条件下，完成预定功能的概率。结构的失效概率是指结构不能完成预定功能的概率，用Pf表示。结构可靠度分析的依据就是根据结构的极限状态计算结构的失效状态的概率。假定式所述两个随机变量的均值和标准差分别为μR、μS和σR、σS，且随机变量均服从正态分布，由此可以获取Z的概率密度函数。......
2025-09-30
相关推荐