在COPA方法的基础上，Tibshirani等人在2007年提出的OS方法引入了分位数做启发式规则附加表达值，进行差异表达基因检测。由于差异估算中用正常组样本中值代替了全部数据的中值，ORT方法比COPA方法和OS方法恰当地估计了两组数据的差异。COPA方法和OS方法随差异数目的增加，性能有所降低。Lian在2008年提出的MOST方法隐性地考虑了差异基因表达强度临界值所有可能的取值，通过确定其统计量最大值来确定阈值，从而检测差异表达基因。......
2023-11-21
可靠性方法：基因算法与神经网络的应用
【摘要】：通过引入罚函数的方式，采用遗传算法可求解此类约束优化问题。本书的遗传算法流程是利用某种编码技术，作用于称为染色体的数字串，模拟由这些串组成的群体的进化过程。图5.2遗传算法流程图基于遗传算法的体系可靠度优化设计的步骤如下：编码：编码是指数据的表现型到基因型的映射。在遗传算法中规定适应度值越大的染色体越优。这是遗传算法区别于其他算法的重要特征，是产生新个体的主要方法。
结构体系可靠性优化设计存在三个问题：①工程结构优化一般是约束优化，如何将体系可靠度与约束优化结合起来比较困难；②工程结构的功能函数具有非线性和隐式特点，其可靠度求解困难；③工程结构具有高次超静定特点，失效模式及失效路径繁杂，体系可靠性求解困难。
针对以上难点，本书采用以下思路：通过神经网络将有限元结构分析和MC抽样结合起来计算各失效模式的可靠度，采用β约界法构建失效树，并计算体系可靠指标，最后将体系可靠指标由罚函数的形式引入到遗传算法中，经过多次的选择、交叉和变异得出最优种群，在最优种群中选出最优个体为优化结果。该方法的流程图如图5.1所示。
图5.1 结构体系可靠性优化设计流程图
工程结构优化设计一般以结构重量为目标函数，体系可靠性优化的数学模型可表示为［13］：
式中，X为设计变量；Wj为第j个构件的重量；W为结构总重；g（X）为约束函数；βs和β0分别为结构体系可靠指标和目标体系可靠指标；Xu和Xl分别为设计变量上下限。
通过引入罚函数的方式，采用遗传算法可求解此类约束优化问题。遗传算法的步骤有编码、产生初始群体、计算适应度、选择、交叉、变异等基本操作［14］。针对实际工程结构的多维、高精度的连续函数优化问题，各步骤的参数选取如下：选择浮点编码为编码方式；按式（5.2）随机方法进行种群初始化；以造价或截面面积为适应度函数；选用轮盘赌选择方法、多点交叉方法和变异方法。
X＝（Xu-Xl）×Rand+Xl （5.2）
式中，Rand表示产生（0，1）范围内的随机数。为了使罚函数简单而又达到约束的目的，采用如下所示罚函数：
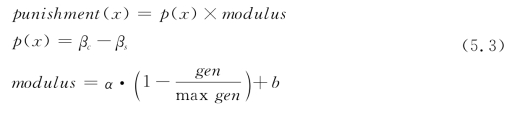
式中，p（x）为结构种群个体与约束产生的违反量；βc为体系可靠指标的目标约束值；βs为种群个体的体系可靠指标；α为惩罚严厉性系数；b为大于0的惩罚参数，由试算得出；惩罚值modulus随着迭代次数的增加而减小；gen为当前迭代次数；max gen为最大迭代次数。
遗传算法（Genetic Algorithm，GA）是借鉴了遗传学说和进化论，模仿自然界生物进化机制而得出的随机搜索算法。它从实际问题的参数集中随机选取得到种群，种群中的个体即为一串符号形式的“染色体”，这些染色体在每一代中用适应度值来测量其优劣性，然后通过选择、交叉、变异运算形成下一代。选择的原则是适应度值越高的，被选择的几率越大，适应度值越低的，被淘汰的概率也越大。经过若干循环后，算法收敛于最好的染色体，它很可能就是问题的最优解。这样的过程体现了生物界的优胜劣汰原则。
本书的遗传算法流程是利用某种编码技术，作用于称为染色体的数字串，模拟由这些串组成的群体的进化过程。它通过有组织的、随机的信息交换来重新组合那些适应性好的串，生成新的串的群体。然后再通过神经网络将有限元结构分析和MC抽样结合起来计算各失效模式的可靠度，采用β约界法构建失效树，并计算体系可靠指标，最后将体系可靠指标由罚函数的形式引入到遗传算法中，经过多次的选择、交叉和变异得出最优种群，在最优种群中选出最优个体为优化结果。如图5.2所示为遗传算法流程图。
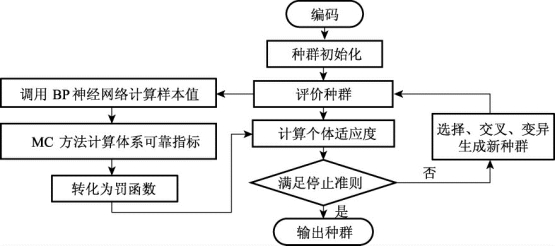
图5.2 遗传算法流程图
基于遗传算法的体系可靠度优化设计的步骤如下：
（1）编码：编码是指数据的表现型到基因型的映射。目前可以用于编码的方法有多参数集联编码、格雷码编码等，但一般会选择两种较简单且常用的编码方式，即二进制编码和浮点数编码。二进制编码方法是遗传算法中最主要的一种编码方式，产生的基因是一个二进制符号序列，每个基因只能取0或1。二进制编码方法操作简单且易行，在进行遗传操作交叉、变异等时便于实现。但当个体编码串的长度较长时，将急剧扩大搜索的空间使得算法操作变得复杂；当个体编码串的长度较短时，便使得精度达不到要求。浮点数编码是指个体的每个基因可以用一个范围内的浮点数来表示。此方法适合表示取值范围比较大的数值，针对实际工程结构的多维、高精度的连续函数优化问题。
根据二进制编码和浮点数编码的对比，本书采用浮点数编码方式。该方法的选择使得对降低采用遗传算法对染色体进行处理的复杂性起到了很好的作用。
（2）种群初始化：指在群体初始化阶段采用生成随机数的方法，对染色体的每一维变量进行随机初始化赋值，这些初始化的染色体构成一个群体。采用公式（5.4）进行计算：
X＝（Xu-Xl）×Rand+Xl （5.4）
式中，Rand表示产生（0，1）范围内的随机数；X表示设计变量。
（3）评价群体：先调用BP神经网络计算样本值，再用MC方法计算个体体系可靠度指标，最后采用罚函数自动调节惩罚比的方式计入到适应度中。这样就将遗传算法中的有约束条件的最优问题转化为无约束条件的优化问题，使得计算的适应度也就是目标函数得以实现，也保证了结构的可靠性。
（4）计算适应度：在遗传算法中用评估函数来评估各个染色体的优劣。评估函数通常根据实际的问题来确定。在遗传算法中规定适应度值越大的染色体越优。如果优化问题是求解最大值，则可以直接套用问题定义的函数表达式，但对于求解某个函数的最小值时，可对目标函数进行以下变换：
Eval（C）＝-f（X） （5.5）
式中，Eval（·）是评估函数；X为随机变量；C为X的染色体；f（·）为目标函数。本书采用目标函数的变换形式作为评估函数，表达式为：
Eval（C）＝-W（X） （5.6）
（5）选择：为了避免遗传信息的丢失和提高全局计算效率，适应度较大的个体被遗传到下一代群体中的概率较大，有轮盘赌、随机竞争和最佳保留等方法。本书选取轮盘赌方法。
（6）交叉：两个配对的染色体按某种方式相互交换部分基因，从而形成新的个体。这是遗传算法区别于其他算法的重要特征，是产生新个体的主要方法。其方法有单点交叉、多点交叉和均匀交叉等。
（7）变异：以较小的概率改变编码的某些部位值，从而生成新的个体来改变遗传算法的局部搜索能力和维持群体的多样性。
实际工程结构具有高次非线性的隐式功能函数，要找出所有的失效模式，并用传统的一次二阶矩法（FOSM）和MCM实现其可靠度求解极其困难。事实上，采用神经网络和有限元方法可以映射出随机变量与单元应力和节点位移关系，然后用MCM对训练好的神经网络抽样分析，可以求解且具有高次非线性的隐式功能函数的失效概率，其神经网络构建过程如图5.3所示。
图5.3 神经网络构建流程图
构建神经网络的目的是为了精确映射出结构各个隐式功能函数，即各随机变量与有限元分析结果（应力、位移等）之间的关系［15］。神经网络训练完成且满足精度要求后输出，在遗传算法主程序中被调用，因此神经训练过程并不参与遗传算法的循环过程，这也大大减少了计算时间。神经网络的精度决定了优化结果的准确性，为了使其满足要求，从样点选取、数据归一化和神经网络选取方面寻求更高效的神经网络构建方法。
（1）样本点选取：选取足够多的神经网络样本点数据才能保证其拟合精度，但考虑到实际工程应用的要求，样本点应尽量少。均匀设计［16］（UD）将样本点严格按照度量准则充分均匀地分布在设计空间上，可大大减少样本点数。因此与正交设计相比，UD方法具有更好的均匀性，而且同样试验次数可以安排较多的水平数。由于文献［16］提供的均匀设计表格最高水平数仅为37个，本书采用DPS（数据处理系统）的均匀试验设计功能，通过多次迭代实现具有多因素和更多水平数的均匀试验设计方案。
（2）数据归一化：RBF网络的映射函数为：
uj的表达式如式（5.9）所示，由于f（uj）∈（0，1），而实际的样本值不一定在此范围内，因此各样本值需按式（5.8）归一化处理，归一化后的z′f为：
式中，zf为原始数据值；min和max分别为数据最小值和最大值。
（3）神经网络选取：选取逼近能力、分类能力、泛化能力和学习速度等方面均优于BP神经网络的RBF神经网络，其核函数为高斯函数［17］：
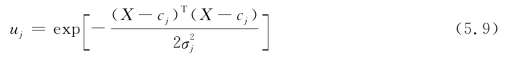
式中，cj和σj为RBF网络数据中的均值和标准差；T为求范数的转置矩阵。
如式（5.9）所示RBF网络的隐层神经元将依据其输入距离高斯函数中心点的远近来决定它的兴奋程度，更加深刻地反映生物神经系统的本质。RBF神经网络可以根据精度要求逐步增加神经元数量，但为了提高泛化能力，避免陷入局部最优，要选取合适的梯度步长和精度要求。
实际工程结构一般存在大量的失效模式，通过β约界法可以寻找各个主要失效模式；再将各失效模式通过一定的串并联关系，求解体系可靠度。神经网络训练完成后，在遗传算法的主程序中调用该网络，计算体系可靠度。
针对单个失效模式的可靠度计算，为保证计算结果的可靠性，若β0为目标可靠指标，则样本点数量N应满足以下关系：
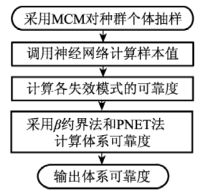
图5.4 体系可靠度计算流程图
利用建立好的RBF网络预测每个随机样本的功能函数值，并统计功能函数值f＜0的个数Nf，则可靠指标为：
式中，norminv表示正态累积分布函数的反函数。
采用Thoft-Christensen提出的β约界法［18］，则候选失效单元应满足以下要求：
βi＜βmin+Δβ （i＝1，…，n） （5.12）
式中，βi为各杆件的可靠指标；βmin为所有βi的最小值；Δβ在第一层次的失效单元选取时取3，以后取1。
假设结构所有的失效模式表示为Ei，i＝1，2，…，n，其中E1包含
个相继失效的失效状态；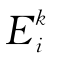
表示第i个失效模式的第k个失效状态；Es表示体系失效，则［18］：
式中，单个失效模式是由各失效状态并联而成，而体系失效是由各失效模式串联而成。当失效模式仍然较多时，采用概率网络估算技术［18］（PNET）方法对失效模式进行归类。
有关桥梁可靠度分析方法与应用的文章
- 详细阅读
-
人工神经网络和遗传算法方法的详细介绍详细阅读
机器学习方法已表现出很好的解释复杂生态数据序列的能力，并能按照模型的形式将这些解释进行综合。在此将详细介绍两个机器学习方法：人工神经网络；遗传算法一、人工神经网络人工神经网络对于分析复杂的数据序列是一个很好的工具，并在多数情况下优于数理统计方法。......
2023-11-17
-
桥梁可靠性分析方法与应用详细阅读
由设计结构的内力分析可知，H1和H7的内力较小，可忽略其失效特性。表5.4钢桁梁结构静力计算结果选取纵梁、横梁弯曲失效E1，受压腹杆屈曲失效E2和受拉腹杆拉应力失效E3这3种失效模式。由图5.12可以看出，设计结构的最初失效状态表现为H3和H6杆件的屈曲失效，最终失效状态表现为L1和L2杆件弯曲失效后在跨中位置形成塑性铰，而出现不适宜加载的过大变形。图5.12钢桁梁结构失效树......
2023-09-19
-
Spark+Hadoop机器学习算法在基因表详细阅读
Spark技术为基于内存的开源计算，Spark生态系统在机器学习领域的重要应用MLlib具有很多常用算法，实现了K-means等多种分布式机器学习算法。本章探讨Spark+Hadoop技术的机器学习的深度和广度提升了大数据分析的效率，适应迭代式机器学习模型的特定需求，分析数据中的关系以获得规律来预测新样本，对数据进行收集、统计和分析。......
2023-11-21
-
多基因编码改进遗传算法在多飞行器协同制导与控详细阅读
第2步，针对第1、2行设定的目标和任务，从能够执行此任务的无人机集中选择某无人机作为无人机行，完成目标基染色体的第3、4行编码。至此，完成一个完整的目标基染色体的编码。图2-3无人机基染色体编码示例3.遗传算子采用带精英策略的轮盘赌选择算子将本代中适应度值最好的Ne个个体直接选择到下一代种群中，不参与交叉和变异操作。......
2023-08-02
-
神经网络方法在桥梁可靠度分析中的应用详细阅读
人工神经网络在最近几十年里无论是在理论或是在应用上的研究都取得了很大的进展。此外，神经网络具备良好的泛化能力，相比传统的多项式响应面方法精度和效率更高。常规神经网络的结构如图3.1所示。图3.1神经网络示意图人工神经网络主要有以下几种较为常见的类型：反向传播-BP神经网络。BP网络是一种遵循误差逆向传播算法训练得到的多层前馈式网络，也是当前应用较广泛的ANN之一。......
2023-09-19
-
控制算法的解析与运行-现场总线与应用技术详细阅读
在上位机将控制算法传输到控制卡后，控制卡会将控制算法信息暂存到控制算法缓冲区，并不会立即对控制算法进行解析。所以，控制算法的解析必须选择合适的时机。本系统中将控制算法的解析操作放在本周期的控制算法运算结束后执行，这样不会对本周期内的控制算法运行产生影响，新的控制算法将在下一周期得到执行。上位机下发给控制卡的控制算法包含控制算法的操作信息、回路信息和回路中各功能模块信息。......
2023-11-22
-
标准粒子算法的应用与实践详细阅读
粒子群算法和其他的进化算法类似， 也是根据群体对环境的适应度， 将个体选择更好的区域进行移动。在标准的粒子群算法中， 粒子的速度和位置的变化可由公式(6-1)和公式(6-2)计算获得。标准的粒子群算法流程分为以下几个步骤：初始化种群。需要随机产生群体中所有粒子的初始速度和位置， 确定粒子的pbest 和gbest。......
2023-06-20
相关推荐