【摘要】:为了表明ASVR算法在实际工程中的应用,选取主跨为420m的预应力混凝土斜拉桥为工程背景。图4.19CNA34拉索失效前后CNA33索力响应面图4.20斜拉桥的3层失效树斜拉索在运营期会出现抗力随时间的增长而退化的现象,锈蚀和疲劳是拉索抗力退化并导致拉索强度失效的主要因素。图4.21斜拉索锈蚀和疲劳对可靠度影响ECBA34表示北塔岸侧34号斜拉索失效事件;ECBA33为条件概率事件,表示北塔岸侧34号斜拉索失效后33号斜拉索失效事件。
为了表明ASVR算法在实际工程中的应用,选取主跨为420m的预应力混凝土斜拉桥为工程背景。采用ANSYS软件建立全桥整体有限元模型,其中主梁和索塔单元为Beam44梁单元,斜拉索为Link10杆单元。全桥主要构件的编号如图4.14所示,单位为m。

图4.14 某斜拉桥的桥型布置及主要构件编号图
该斜拉桥的主要失效模式有:结构稳定失效、斜拉索强度失效、主梁和索塔的截面弯曲失效以及主梁跨中位移超限失效等[23-24]。为了方便描述ASVR方法在斜拉桥算例中的应用,选取承载能力极限状态下的斜拉索强度失效、主梁和索塔截面弯曲失效为构件的主要失效模式。斜拉桥算例主要选取承载能力极限状态下的前两种失效模式。由于斜拉桥存在较大的轴力效应,主梁和索塔单元均为压弯构件,据此建立的功能函数表达式为:
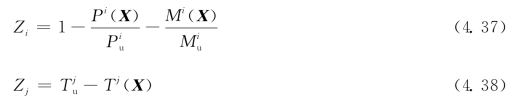
式中,随机变量X其统计参数如表4.8所示; 为第i个梁单元的轴力抗力和弯矩抗力;Pi(X)和Mi(X)为第i个梁单元的轴力和弯矩效应值;
为第i个梁单元的轴力抗力和弯矩抗力;Pi(X)和Mi(X)为第i个梁单元的轴力和弯矩效应值; 和Tj(X)分别为第j根斜拉索的抗力值和效应值。荷载为双向四车道的公路-Ⅰ级汽车荷载。朱劲松等[25]的研究结果表明,在仅考虑中跨均布荷载作用下斜拉桥的可靠指标较低,因此,本书将车辆荷载转换为跨中均布荷载。
和Tj(X)分别为第j根斜拉索的抗力值和效应值。荷载为双向四车道的公路-Ⅰ级汽车荷载。朱劲松等[25]的研究结果表明,在仅考虑中跨均布荷载作用下斜拉桥的可靠指标较低,因此,本书将车辆荷载转换为跨中均布荷载。
表4.8 斜拉桥随机变量的统计参数
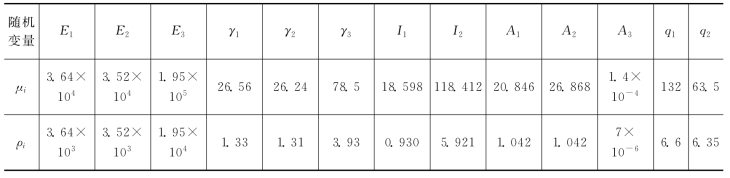
表中,E1、E2、E3分别表示主梁、索塔、斜拉索的弹性模量(MPa);γ1、γ2、γ3分别表示主梁、索塔和斜拉索的容重(kN·m-3);I1、I2分别表示主梁和索塔的惯性矩(m4);A1、A2、A3分别表示主梁、索塔和斜拉索的面积(m2);q1、q2分别表示二期恒载的单位长度重量和汽车荷载的单位长度荷载(kN·m-1);弹性模量、容重和二期恒载服从正态分布,截面惯性矩与面积服从对数正态分布,汽车荷载服从极值Ⅰ型分布。根据如图4.8所示悬吊结构的失效准则,暂定体系失效准则为包含主梁或索塔弯曲失效在内的3个构件失效。根据第一次模型更新步骤得出斜拉索的可靠指标,如图4.15所示。

图4.15 斜拉索的可靠指标

图4.16 拉索对索塔T2截面弯矩的影响系数

图4.17 拉索对主梁GBJ34截面弯矩的影响系数
由图4.15可知,该斜拉桥端索的可靠指标较小,因此在失效路径的第一阶段选取边跨和中跨端索(编号为CBA34、CBJ34、CNJ34和CNA34)为失效构件。斜拉索失效对索塔和主梁关键截面的弯矩影响如图4.16和图4.17所示。边跨拉索对索塔T2截面弯矩较为敏感,而中跨拉索对主梁GBJ34截面较为敏感,且随着拉索编号的减小敏感系数逐步减小。由此可知该斜拉桥的失效路径为南、北塔边跨拉索失效后导致索塔T2截面弯曲失效和中跨拉索失效后导致主梁GBJ34截面弯曲失效。更新支持向量方法可得出该斜拉桥的4条主要失效路径及条件可靠指标,如图4.18所示。将如图4.18所示失效路径通过串并联关系得出结构体系失效概率计算图。

图4.18 全桥主要失效路径(https://www.chuimin.cn)
筛选出失效概率较高的斜拉索,根据流程图中第二次模型更新步骤搜索剩余结构的主要失效构件。其中,CNA34拉索失效前后,CNA33拉索索力与汽车均布荷载q2和拉索截面面积As的响应面如图4.19所示。由此得出的4条主要失效路径及其失效树如图4.20所示。图中,Es为结构体系失效事件,对应的体系可靠指标为7.31,ECBA34表示北塔岸侧第34号斜拉索失效事件,对应的条件可靠指标为4.85。由图4.18可知,该斜拉桥的两类主要失效路径分别为边跨拉索失效(ECBA34,ECNA34,ECBA33,ECNA33)导致索塔弯曲失效(ET2),中跨拉索失效(ECBJ34,ECNJ34,ECBJ33,ECNJ33)导致主梁根部截面弯曲失效(EGBJ1,EGNJ1)。

图4.19 CNA34拉索失效前后CNA33索力响应面

图4.20 斜拉桥的3层失效树
斜拉索在运营期会出现抗力随时间的增长而退化的现象,锈蚀和疲劳是拉索抗力退化并导致拉索强度失效的主要因素。文献[26]由串并联方式得出某根拉索在20年内的斜拉索的均值系数和标准差系数表达式分别为:

式中,t为以年为单位的时间变量。拉索抗力均值系数随时间增长而降低,标准差系数则相反。文献[27]建立了考虑微动疲劳的钢绞线斜拉索抗力退化模型,其函数表达式为:

式中,t表示以年为单位的时间变量;斜拉索退化函数是为后文参数分析提供依据,并不具有代表性。实桥评估时应采用具有针对性的斜拉索检测数据。
由于该斜拉桥的体系失效事件均是由两对斜拉索失效导致,斜拉索的可靠指标对结构体系可靠指标有较大的影响。分别考虑斜拉桥锈蚀和疲劳导致斜拉索抗力退化,重新评估斜拉索的可靠指标,再更新如图4.20所示的失效树,得出体系可靠指标,如图4.21所示。

图4.21 斜拉索锈蚀和疲劳对可靠度影响
ECBA34表示北塔岸侧34号斜拉索失效事件;ECBA33为条件概率事件,表示北塔岸侧34号斜拉索失效后33号斜拉索失效事件。拉索锈蚀导致斜拉索抗力退化对斜拉索的可靠度有较大的影响,由此可得到拉索锈蚀和疲劳损伤对体系可靠度的影响,如图4.22所示。

图4.22 斜拉索锈蚀和疲劳对体系可靠度影响
图中各时间点的竖线两端为体系可靠指标上下限,连接上下限的中点形成了体系可靠指标的下降趋势曲线。在考虑斜拉索抗力退化的情况下,斜拉索锈蚀和疲劳损伤产生斜拉索抗力退化致使体系可靠度指标呈加速下降趋势。斜拉索锈蚀对体系可靠度指标影响较大,锈蚀产生的拉索抗力退化是导致斜拉桥在运营期体系可靠度下降的重要因素。斜拉索的养护和及时更换对保证斜拉桥在运营期体系可靠度安全水平具有重要的意义。


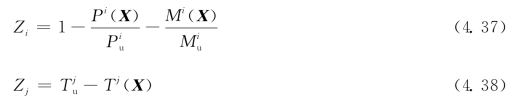
 和T
和T















相关推荐