桥梁可靠度分析方法：结构体系失效模型

2025-09-30 理论教育版权反馈

【摘要】：塑性铰与失效机构是工程结构构件失效的常见失效模型。塑性铰的出现影响到结构的刚度，导致结构丧失抗力，使结构成为机动结构。图4.6单跨刚架的结构失效示意图结合实际桥梁结构进行体系可靠性分析时，无需面面俱到地去分析。由n个构件组成的超静定桁架结构，可能会有种失效模式。，rp称为部分失效路径。当某一刚架结构产生能使结构系统成为机构的塑性铰组合后，就将导致结构系统丧失承载能力，进而失效。

塑性铰与失效机构是工程结构构件失效的常见失效模型。塑性铰的出现影响到结构的刚度，导致结构丧失抗力，使结构成为机动结构。连续刚构桥在外荷载作用下，当主梁的某一截面产生无约束的塑性变形时，将使该节点左右两边的截面发生相对转动。所以塑性铰定义就是允许结构产生转动的铰。塑性铰的位置一般出现在最大弯矩的截面上，例如：节点附近、集中力作用处和均布荷载的剪力为0处。

在超静定结构中，若使其成为具有1个自由度的失效机构，则需要形成塑性铰的个数r要比它的超静定次数多一些。当结构的超静定次数为s时，塑性铰的个数为r＝s+1。连续刚构桥类似于刚架结构，除基本失效机构外，它的失效机构还可由基本失效机构叠加成失效机构，所有叠加机构（也可能是失效机构）与基本机构对应的破坏荷载的最小值即为刚架的极限荷载。

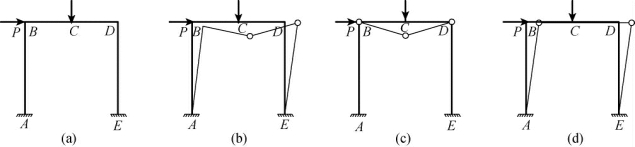
pagenumber_ebook=61,pagenumber_book=51

图4.6　单跨刚架的结构失效示意图(https://www.chuimin.cn)

结合实际桥梁结构进行体系可靠性分析时，无需面面俱到地去分析。如果略去了分析的重点，也给计算结果带来很大的误差。因此，要抓住桥梁分析时的特点，比如桥梁结构可以简化成刚架和桁架，然后利用这些简化结构的特征去分析就会达到实用的目的。当构成静定桁架的构件的拉力或压力超过极限轴力时，该构件就会失效，结果会引起整个结构的失效，而且失效模式的数目与构件的数目相同。然而，超静定桁架和静定桁架有所不同，其分析过程比较复杂，单个构件的失效一般不会引起整个结构体系的失效。若结构超静定次数为s，则任意的（s+1）个构件失效后，整个结构体系一定会失效。由n个构件组成的超静定桁架结构，可能会有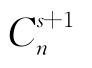 pagenumber_ebook=62,pagenumber_book=52 种失效模式。

对超静定桁架进行可靠性分析时，还必须考虑到一些特征。比如：结构体系的失效概率是组成失效模式的各个失效构件的联合失效概率；与串并联电路等其他分析方法不同的是，超静定桁架的其他构件的内力会随着任一构件的失效而发生变化；当改变失效构件的失效顺序时，就会有不同的失效路径出现，各种失效路径的失效概率也各不相同；设某一失效形式的构件完全失效路径为r1，r2，…，rp，…，rq，而其中的一部分，如r1，r2，…，rp称为部分失效路径。

当某一刚架结构产生能使结构系统成为机构的塑性铰组合后，就将导致结构系统丧失承载能力，进而失效。不同构件的塑性铰产生的顺序不同，会产生不同的失效形式。刚架结构与桁架结构不同的是，它有冗余塑性铰和基本塑性铰。通常采用以下假定：只有构件连接处或集中荷载作用节点处才有塑性铰形成；由于材料的力学行为是完全弹塑性的，因此正常工作的截面则表现为完全弹性，而已经形成塑性铰的截面服从塑性变形理论；塑性铰形成的条件是由屈服函数中单元抗力和荷载效应决定的，抗力在需要时要考虑时间的变化，荷载效应要考虑弯矩、剪力和轴力的综合影响。不能简单地认为，某单元失效后，剩余各单元应力不变，实际上各单元刚度矩阵已经发生变化，也就是说，每个构件失效后，应重新进行计算分析，直至整个结构变为机动结构，不能满足预定的功能要求，此时各失效构件组成一个失效模式，如图4.6所示。

桥梁可靠度分析方法：结构体系失效模型

相关推荐