图3.5结构体系可靠性评估软件的流程图基于MATLAB语言平台的GUI功能,将图3.5所示的计算流程编制评估软件,主界面如图3.6所示。为了帮助用户更好地使用该软件,特编写用户手册。本软件采用纯M文件代码编写,因此界面不受GUI版本限制。图3.6中,菜单栏从左至右分别为:“参数”、“迭代数据”、“RSM数据”、“ANN数据”和“帮助”。“串关联”表示各构件之间是串关联关系。表3.2操作键及功能......
2023-09-19
本书所提出的结构体系可靠度联合算法的流程如图3.3所示。
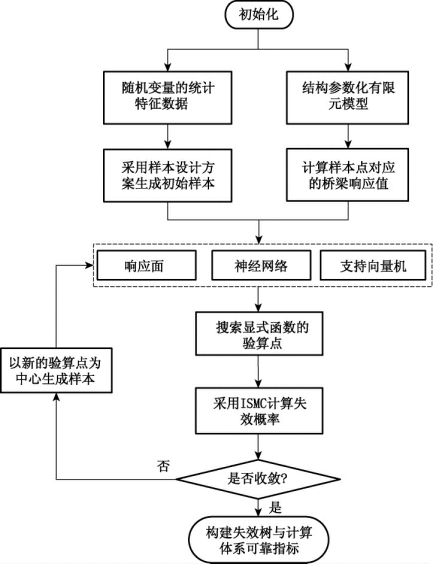
图3.3 结构体系可靠度评估的联合算法流程图
如图3.3中,ISMC表示重要抽样法,该联合算法的主要分析内容是:有限元分析、响应面/神经网络/支持向量机的函数拟合、搜索验算点、计算失效概率。计算效率的关键在于样本点的设计方案以及拟合函数的选取。
训练样本点的好坏直接影响到RBF网络精确度的高低,应从样本点的取值范围及分布方式着手,使样本点均匀散布在样本空间。该子步骤的主要内容为:首先确定随机变量的取值范围,由于实际工程结构的随机变量较多为正态分布,根据3σ原则,数值分布在区间(μ-3σ,μ+3σ)的概率为99.74%,能够满足分析要求;然后按照均匀设计的方法安排试验数据;最后选择合适的RBF神经网络参数进行训练。
在搜索验算点方面,结构可靠指标计算中验算点搜索就是求解以下最优问题:

式中,假定随机变量X的个数为n;ui是由Rosenblatt变换[10]得到的标准正态空间点;d为验算点到标准正态空间原点的距离;Z(X)为功能函数。
针对式(3.7)所示的约束优化问题,文献采用外罚函数的方式将约束优化转变为无约束优化问题,然后采用GA实现求解。该方法适用范围广泛,但该方法迭代过程收敛慢,甚至无法完成优化。相对于遗传算法而言,离子群优化算法的优点是需要调整的参数少,而且不需要梯度信息,因此简洁且易于实现。针对离子群算法易陷入局部极值点、进化后期收敛速度慢、精度低的缺点,存在很多改进方法,如混沌离子群算法、离子群算法与差别进化算法的混合方法等。
由于直接抽样MCS所得到的随机样本点多集中在联合概率密度函数最大值附近,因此样本点多位于可靠域。针对实际工程结构失效概率较小的问题,则需要较多的抽样次数,样本点计算较为困难。事实上,可以用方差缩减技术,减小样本点的数量,同样能达到精确度要求。常用的方法有重要抽样、方向抽样、条件期望抽样和分层抽样等。重要抽样是通过改变抽样中心,使样本点有较多机会落入失效域。
ISMC表示重要Monte Carlo抽样,对应的失效概率无偏估计表达式为:
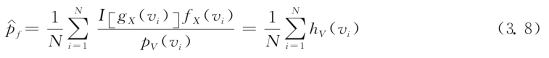
式中,N为抽样次数;I[·]为示性函数;gX(vi)为样本点vi对应的功能函数值;pX(vi)和fX(vi)分别为样本点vi对应的原概率密度函数值和新概率密度函数值;hV(vi)为重要抽样总体hV(v)中的一个样本值。
由数理统计知识可知,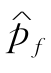 的相对误差为:
的相对误差为:

式中,pf为失效概率的真实值;uα/2为显著水平; 为失效概率估计值
为失效概率估计值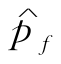 的变异系数。当
的变异系数。当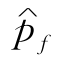 的误差小于20%的概率大于95%时,ε=0.2,uα/2=1.96。由式(3.9)可知,在满足可靠指标具有一定精度的条件下,N的取值应满足以下关系:
的误差小于20%的概率大于95%时,ε=0.2,uα/2=1.96。由式(3.9)可知,在满足可靠指标具有一定精度的条件下,N的取值应满足以下关系:
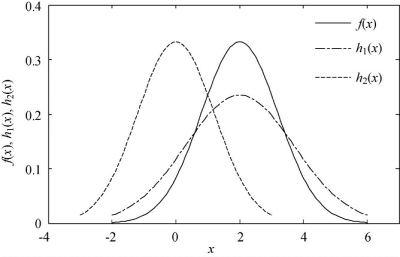
图3.4 概率密度函数f(x)、h1(x)和h2(x)之间的关系
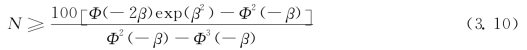
式中,β为可靠指标的精确值。如图3.4给出了两种重要抽样密度函数h1(x)和h2(x)与原始概率密度函数f(x)的图形。
有关桥梁可靠度分析方法与应用的文章

图3.5结构体系可靠性评估软件的流程图基于MATLAB语言平台的GUI功能,将图3.5所示的计算流程编制评估软件,主界面如图3.6所示。为了帮助用户更好地使用该软件,特编写用户手册。本软件采用纯M文件代码编写,因此界面不受GUI版本限制。图3.6中,菜单栏从左至右分别为:“参数”、“迭代数据”、“RSM数据”、“ANN数据”和“帮助”。“串关联”表示各构件之间是串关联关系。表3.2操作键及功能......
2023-09-19

静定桁架就属于这种结构体系,单元逻辑图如图4.2所示。因尔,从体系可靠度的角度来看,实际的桥梁应尽量避免做成静定结构,条件允许时,应做成具有适当冗余度的超静定结构。超静定结构就是具有这种特性的结构体系。......
2023-09-19

BS5400规范[4]将常幅疲劳极限ΔσL定义为当循环次数N=107时对应的容许应力幅值。BS5400规范对不同细节S-N曲线参数规定如表8.1所示。表8.1BS5400规范对疲劳细节S-N曲线参数表8.2BS5400规范的部分疲劳细节分类BS5400规范的特点是规定了常幅疲劳极限,并且基于概率水平给出了结构构造细节在5种失效概率下的S-N曲线。......
2023-09-19

工程结构可靠度是指在规定的时间内,在规定的条件下,完成预定功能的概率。结构的失效概率是指结构不能完成预定功能的概率,用Pf表示。结构可靠度分析的依据就是根据结构的极限状态计算结构的失效状态的概率。假定式所述两个随机变量的均值和标准差分别为μR、μS和σR、σS,且随机变量均服从正态分布,由此可以获取Z的概率密度函数。......
2023-09-19

取目标体系可靠指标β0=2,截面及荷载变异系数均为ξ=0.1,遗传算法优化结果如图5.7所示。图5.7遗传算法迭代过程图由图5.7所示桁架结构遗传算法优化过程可以看出,在第40次种群迭代时,适应度值已经稳定并达到收敛,表明优化过程稳定,优化结果可靠。表5.3不同方法优化结果由表5.3所示的不同体系可靠度约束优化结果可以看出,体系可靠性优化后结构的重量较常规优化方法的大。......
2023-09-19

桥梁结构体系主要失效模式识别方法有两个核心内容,首先是要识别结构的失效状态逐步转移;其次是形成整个结构的失效树。Thoft-Christensen[9]认为约界可以限制分支的操作,它的目的就是将失效树的主干和主枝逐个识别出来,以便组合起来进行体系可靠度的计算。董聪等[11]提出的修正β约界法是工程上较实用的一种方法。修正β约界法的基本原理是,假定由n个单元组成的结构体系中,有r1,r2,…......
2023-09-19

定义若r>3,则无论结构的响应是宽带过程还是窄带过程,Possion假定均能满足精度要求。下面给出考虑密集车辆占有率的Possion假定动力可靠度表达式:由式可计算出界限跨越率和考虑车辆运行状态的大跨度桥梁位移动力可靠度。......
2023-09-19

Rocco等[4]提出了联合SVM和MCS求解结构可靠度的方法。SVM在结构体系可靠度分析中的应用较少。为了发展工程结构体系可靠度理论与方法在桥梁安全评估中的应用,本章将建立桥梁结构体系可靠度分析的简化模型,总结现有结构体系可靠度分析方法,提出基于支持向量机的桥梁结构可靠度分析方法,最后采用两个算例分析表明支持向量机在桥梁结构体系可靠度评估中的应用。......
2023-09-19
相关推荐