响应面法在确定性分析和可靠性分析间搭起了一座桥梁，它能够较好地将常用的可靠度分析方法运用到实际工程结构的可靠度分析中［5］。响应面法的基本思想是通过一系列确定性的试验拟合一个响应面来模拟真实的极限状态曲面，建立参数输入与结构响应之间的关系，并将隐式的功能函数显式地表达出来。这个纯经验的响应面近似拟合技术的关键是在何处用响应面法拟合来替代实际的极限状态曲面。......
2023-09-19
桥梁可靠度分析-二次序列响应面方法
【摘要】：第二章讲述了二次序列响应面方法的一般步骤，本节将就该方法与有限元的联合算法进行阐述。响应面法的基本思想是在真实的响应曲面上取出合适的样本点，通过回归分析，拟合出一个近似的曲面。Bucher［1］提出了采用二次序列函数为核函数的二次序列响应面方法。二次序列响应面法在实际工程结构可靠度分析中应用的关键在于响应面函数所需样本点的设计与选取，这将直接影响该算法的计算效率。表3.1均匀设计表
第二章讲述了二次序列响应面方法的一般步骤，本节将就该方法与有限元的联合算法进行阐述。响应面法的基本思想是在真实的响应曲面上取出合适的样本点，通过回归分析，拟合出一个近似的曲面。在一定的区域内，拟合的近似曲面可代替真实结构响应函数，用以分析新的参数数据下结构的响应。Bucher［1］提出了采用二次序列函数为核函数的二次序列响应面方法。
二次序列响应面法在实际工程结构可靠度分析中应用的关键在于响应面函数所需样本点的设计与选取，这将直接影响该算法的计算效率。样本点的选取方案可采用试验设计（Experiment Design，ED）方法完成［2］，其目的是在样本空间中选取试验点的位置与数量，从而确定拟合响应面函数系数值。下文将从目前使用较多的中心复合设计方法、因子设计法、正交设计法、均匀设计法等方面介绍样本点设计方法。
目前较为广泛使用的是Bucher提出的中心复合设计（Central Composite Designs，CCD）方法。中心复合设计方法被广泛应用于各类工程结构的响应面拟合与可靠度分析。该法是由学者Bucher和Bourgund［1］从选点的角度提出的一种新的方法，其主要是参照响应面法中不含交叉项而推导出来的。假设拥有n个随机变量，那么可以按照设计：假设选择一个中心点x，轴点2n个，则共有（2n+1）个样本点。其样本点是以一个中心点为实验区域的中心点，然后在其中心点两侧选取轴点，因为此方法含有（2n+1）个待定系数，所以Bucher设计法含有较多的样本点数，可以有效地利用实验从而减小实验的次数。
中心复合设计法也称Box-Wilson设计法［3］，其布点的依据是根据Bucher设计法，在Bucher设计法点的基础上另外再增加2n个点，这个时候就形成了三维的立方体，该法与二次响应面法（通过二次功能函数进行拟合的）非常相近，该法的数学表达式如下：
析因设计法也称因子设计法，其考虑的因素有两个甚至更多［4］。析因设计法又被分为两个类型：全面的实验设计法和部分的因子设计法。相对全面实验设计法而言，部分因子设计法主要是考虑各个因素，以及多个因素之间的相互组合。对于全面实验设计的处理，一般根据其水平因素进行布点，其核心内容为把一个空间分割成很多个矩形网格线，然后将每个实验点布置在矩形的顶点处，故其又称为网格设计。
正交设计法是基于考虑很多因素的一种优化设计法，其宗旨是在全面的实验数据中选取样本（具有代表分析的数据）。根据以往设计好的正交表来规划实验设计，其中正交表一般可以划分为n个列数（因素数），n个行数（实验点的数目），而a为全面实验设计法依据因素得到的变量参数。
随着计算机技术与概率统计理论的发展，均匀设计（Uniform Design，UD）法在试验样本点设计方面表现出了突出的优势［5］。均匀设计法是我国学者方开泰［6］和王元共同提出的一种关于均匀方案的实验设计法，并按照所推荐的表格进行排序。自20世纪末以来，均匀设计法在理论研究上有了很多新的发展和创新，同时该法也在可靠度分析法中得到了广泛的使用。其与正交设计法相比，均匀设计样本的优势主要表现在：平均分散、整齐可比。均匀设计法的宗旨目标是减少研究的样本数量，通常我们只在其试验范围内进行平均分散、整齐比较。故做该设计实验时，一般将实验点平均分散在整个实验中。而均匀设计法相对其他实验方法的优点是在一定相同的条件之下，所进行的实验次数最少，同时因素的最大水平数也最小。该方法的本质是在试验范围内挑选出具有代表性质的试验点。与正交设计法的主要区别在于均匀设计样本点具有“均匀分散、整齐可比”的特点。因此，均匀设计是仅考虑试验点在试验范围内的均匀散布的一种试验方法。
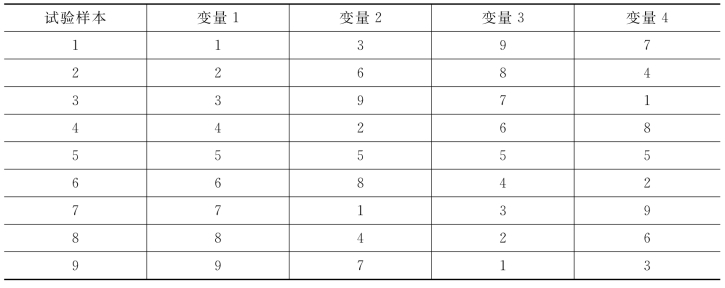
假定因素个数为m，每个因素有n个水平，那么这个时候均匀设计法对于样本的选取只用n个。故它不仅能够有效对实验组合进行严格的控制，而且不会增加实验设计的工作，综合考虑这些优点，均匀设计法已经被广泛地应用在很多实验设计中。但是均匀设计也有其缺点，其不能很好地对结果进行直观判断，此时必须根据数据进行统计以及分析。表3.1给出了一张均匀设计表。
表3.1 均匀设计表
有关桥梁可靠度分析方法与应用的文章
- 详细阅读
- 详细阅读
-
桥梁可靠度分析方法-桥梁可靠度分析方法与应用详细阅读
静定桁架就属于这种结构体系，单元逻辑图如图4.2所示。因尔，从体系可靠度的角度来看，实际的桥梁应尽量避免做成静定结构，条件允许时，应做成具有适当冗余度的超静定结构。超静定结构就是具有这种特性的结构体系。......
2023-09-19
-
桥梁动力响应概率分析的可靠度方法与应用详细阅读
Chen等［53］的研究结果表明，车流通过桥梁时，车辆与桥梁之间的互相作用力受前后车辆的影响较小，因此可单独提取每个车辆与桥梁的相互作用力的时变力。采用上述EDWL方法可将车辆的每个轴重转换为等效的时变集中力，这样为基于有限元的桥梁动力响应瞬态分析提供了有利条件。图6.17随机车流作用下车-桥耦合振动分析流程动力响应的概率统计分析方面，在ANSYS平台加载随机车流的流程如图6.17所示。......
2023-09-19
-
桥梁抽样方法分析-桥梁可靠度分析方法与应用详细阅读
一般的MC法用于高度非线性的极限状态曲面或者随机变量维数较高的情况，使用在笛卡儿坐标下的抽样模拟法效率较低，计算耗时较多。因此，Ditlevsen、Olesen、Mohr提出了在标准正态空间中极坐标下进行抽样的方向抽样MC法。③重复步骤①和②直到N次，利用式估计失效概率。对于极限状态曲面接近球面的情况，方向抽样MC法比笛卡尔坐标空间的MC法占较大的优势，若计算接近平面的极限状态曲面时，则无优势。......
2023-09-19
-
优化结果分析-桥梁可靠度分析方法与应用详细阅读
取目标体系可靠指标β0＝2，截面及荷载变异系数均为ξ＝0.1，遗传算法优化结果如图5.7所示。图5.7遗传算法迭代过程图由图5.7所示桁架结构遗传算法优化过程可以看出，在第40次种群迭代时，适应度值已经稳定并达到收敛，表明优化过程稳定，优化结果可靠。表5.3不同方法优化结果由表5.3所示的不同体系可靠度约束优化结果可以看出，体系可靠性优化后结构的重量较常规优化方法的大。......
2023-09-19
-
桥梁可靠度分析中的车-桥动力响应研究详细阅读
鲁乃唯［3］在随机车流作用下悬索桥的动力响应概率模型以及动力可靠度评估方面的研究取得一定成果，但未考虑到由于路面平整度引起的桥梁随机振动因素。汽车荷载的密集与稀疏运行状态对桥梁产生的动力响应具有显著差异，对于桥梁的评估，需要考虑运营期内汽车荷载引起的极值响应。......
2023-09-19
-
桥梁可靠度分析方法及应用详细阅读
Rocco等［4］提出了联合SVM和MCS求解结构可靠度的方法。SVM在结构体系可靠度分析中的应用较少。为了发展工程结构体系可靠度理论与方法在桥梁安全评估中的应用，本章将建立桥梁结构体系可靠度分析的简化模型，总结现有结构体系可靠度分析方法，提出基于支持向量机的桥梁结构可靠度分析方法，最后采用两个算例分析表明支持向量机在桥梁结构体系可靠度评估中的应用。......
2023-09-19
相关推荐