第二章讲述了二次序列响应面方法的一般步骤，本节将就该方法与有限元的联合算法进行阐述。响应面法的基本思想是在真实的响应曲面上取出合适的样本点，通过回归分析，拟合出一个近似的曲面。Bucher［1］提出了采用二次序列函数为核函数的二次序列响应面方法。二次序列响应面法在实际工程结构可靠度分析中应用的关键在于响应面函数所需样本点的设计与选取，这将直接影响该算法的计算效率。表3.1均匀设计表......
2023-09-19
改进的二次序列响应面法在桥梁可靠度分析中的应用
【摘要】：由于在下一次迭代时也需要计算的值，因此该次选择并没有增加有限元的工作量，还能减少部分功能函数的迭代次数。
国内外学者都对响应面法进行了深入的研究：Bucher［6］提出一种迭代内插技术使响应面方法具有较好的效率；Moses［7］利用序列响应面法较好地解决了拟合点的问题，并成功应用于飞机翼板可靠度分析；蒋友宝［8］将响应面法与可靠度分析的几何法相结合实现了对大型结构的可靠度分析，并验证了其精度；辛国顺［9］把响应面法与有限元模型的重要抽样的MonteCarlo法结合起来提出一种改进的混合分析法；苗超［10］把响应面法有效地应用在一连续桥梁体系可靠度分析中。他们在响应面法的计算和应用方面都做出了努力，但是如何在满足精度要求的条件下，减少迭代次数，仍是一个值得研究的内容。
在Bucher［6］提出的二次序列响应面法的基础上进行改进，计算步骤如下：
①假定初始迭代点
一般取均值点；
②通过结构有限元等数值方法计算功能函数值
以及
其中f第一步取3，以后取1；
③解线性方程组，得（2n+1）个待定系数，得到以二次多项式表达的近似功能函数，从而确定极限状态方程；
④用可靠度计算器求解验算点x＊（k）及可靠指标β（k）；
⑤计算
（本书精度），如条件满足，经线性插值得到新展开点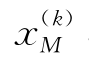
，然后返回②进行下一步迭代，直到β（k）值收敛，则停止迭代；
由于一般结构的极限状态曲面都是非线性的，因此验算点x＊（k）经式（2.29）线性插值得到的新展开点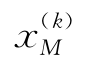
并不一定在极限状态曲面上，而且也并不一定比x＊（k）距离曲面更近一些。所以本书在⑤的基础上加上一次条件选择。
⑥如果
作为下次迭代点，否则将x＊（k）作为下次迭代点。
由于在下一次迭代时也需要计算
的值，因此该次选择并没有增加有限元的工作量，还能减少部分功能函数的迭代次数。
有关桥梁可靠度分析方法与应用的文章
- 详细阅读
-
桥梁可靠度分析方法：响应面法原理详细阅读
响应面法在确定性分析和可靠性分析间搭起了一座桥梁，它能够较好地将常用的可靠度分析方法运用到实际工程结构的可靠度分析中［5］。响应面法的基本思想是通过一系列确定性的试验拟合一个响应面来模拟真实的极限状态曲面，建立参数输入与结构响应之间的关系，并将隐式的功能函数显式地表达出来。这个纯经验的响应面近似拟合技术的关键是在何处用响应面法拟合来替代实际的极限状态曲面。......
2023-09-19
-
神经网络方法在桥梁可靠度分析中的应用详细阅读
人工神经网络在最近几十年里无论是在理论或是在应用上的研究都取得了很大的进展。此外，神经网络具备良好的泛化能力，相比传统的多项式响应面方法精度和效率更高。常规神经网络的结构如图3.1所示。图3.1神经网络示意图人工神经网络主要有以下几种较为常见的类型：反向传播-BP神经网络。BP网络是一种遵循误差逆向传播算法训练得到的多层前馈式网络，也是当前应用较广泛的ANN之一。......
2023-09-19
-
桥梁动力响应概率分析的可靠度方法与应用详细阅读
Chen等［53］的研究结果表明，车流通过桥梁时，车辆与桥梁之间的互相作用力受前后车辆的影响较小，因此可单独提取每个车辆与桥梁的相互作用力的时变力。采用上述EDWL方法可将车辆的每个轴重转换为等效的时变集中力，这样为基于有限元的桥梁动力响应瞬态分析提供了有利条件。图6.17随机车流作用下车-桥耦合振动分析流程动力响应的概率统计分析方面，在ANSYS平台加载随机车流的流程如图6.17所示。......
2023-09-19
-
桥梁可靠度分析中的车-桥动力响应研究详细阅读
鲁乃唯［3］在随机车流作用下悬索桥的动力响应概率模型以及动力可靠度评估方面的研究取得一定成果，但未考虑到由于路面平整度引起的桥梁随机振动因素。汽车荷载的密集与稀疏运行状态对桥梁产生的动力响应具有显著差异，对于桥梁的评估，需要考虑运营期内汽车荷载引起的极值响应。......
2023-09-19
-
桥梁可靠度分析方法-桥梁可靠度分析方法与应用详细阅读
静定桁架就属于这种结构体系，单元逻辑图如图4.2所示。因尔，从体系可靠度的角度来看，实际的桥梁应尽量避免做成静定结构，条件允许时，应做成具有适当冗余度的超静定结构。超静定结构就是具有这种特性的结构体系。......
2023-09-19
-
桥梁可靠度分析与应用详细阅读
BS5400规范［4］将常幅疲劳极限ΔσL定义为当循环次数N＝107时对应的容许应力幅值。BS5400规范对不同细节S-N曲线参数规定如表8.1所示。表8.1BS5400规范对疲劳细节S-N曲线参数表8.2BS5400规范的部分疲劳细节分类BS5400规范的特点是规定了常幅疲劳极限，并且基于概率水平给出了结构构造细节在5种失效概率下的S-N曲线。......
2023-09-19
-
桥梁可靠度分析中的Possion假定详细阅读
定义若r＞3，则无论结构的响应是宽带过程还是窄带过程，Possion假定均能满足精度要求。下面给出考虑密集车辆占有率的Possion假定动力可靠度表达式：由式可计算出界限跨越率和考虑车辆运行状态的大跨度桥梁位移动力可靠度。......
2023-09-19
相关推荐