静定桁架就属于这种结构体系，单元逻辑图如图4.2所示。因尔，从体系可靠度的角度来看，实际的桥梁应尽量避免做成静定结构，条件允许时，应做成具有适当冗余度的超静定结构。超静定结构就是具有这种特性的结构体系。......
2023-09-19
桥梁可靠度分析方法:重要抽样法
【摘要】：重要抽样法的原理就是建立一个重要抽样密度函数hX，将失效概率转化为：式中，对于重要抽样法，在通常的实际工程结构中，满足误差小于20%的置信度为95%条件的模拟次数约为103数量级，抽样次数比直接抽样法少。重要抽样法用于体系可靠度的计算时，结构的体系可靠度涉及多个功能函数，则重要抽样区域较多。在标准正态空间中，笛卡尔坐标系下任意随机向量以pVi对V做Ni次抽样，其中第j个样本为由式可得失效概率Pf的无偏估计值为：
直接抽样法所得随机变量X的样本点xi多集中在联合概率密度函数fX（x）的最大值点附近，而该点一般比较靠近X的均值点μx。实际的结构失效为小概率事件，从而μx处于可靠域而不在极限状态曲面上，在失效域的样本较小，因此该方法计算效率和精度较低。通过改变随机抽样中心，使样本点落入失效域的机会较多，会增加功能函数Z＜0的机会。重要抽样法的原理就是建立一个重要抽样密度函数hX（x），将失效概率
转化为：
式中，
对于重要抽样法，在通常的实际工程结构中，满足误差小于20%的置信度为95%条件的模拟次数约为103数量级，抽样次数比直接抽样法少。
重要抽样法用于体系可靠度的计算时，结构的体系可靠度涉及多个功能函数，则重要抽样区域较多。对于串联体系，每个极限状态曲面都有一个失效可能性较多的点或设计验算点及其监控的重要区域，都应选为抽样中心，考虑到各失效模式对体系失效概率的贡献不同，在进行抽样时则要根据不同区域对体系失效概率的贡献来分配抽样的次数。设串联体系的失效模式有m个，第i个失效模式对应的功能函数为Zi＝gxi（X），失效概率为pfi，可靠指标为βi，则以其验算点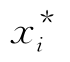
为抽样中心进行抽样时，各功能函数分配的抽样次数为：
式中，int表示取整函数。以第i个验算点为抽样中心的概率密度函数为pVi（v），则
由此可得串联结构体系的失效概率为：
式中，i表示第i个功能函数，j表示第j次抽样。在标准正态空间中，笛卡尔坐标系下任意随机向量
以pVi（v）对V做Ni次抽样，其中第j个样本为
由式（2.23）可得失效概率Pf的无偏估计值为：
有关桥梁可靠度分析方法与应用的文章
- 详细阅读
-
优化结果分析-桥梁可靠度分析方法与应用详细阅读
取目标体系可靠指标β0＝2，截面及荷载变异系数均为ξ＝0.1，遗传算法优化结果如图5.7所示。图5.7遗传算法迭代过程图由图5.7所示桁架结构遗传算法优化过程可以看出，在第40次种群迭代时，适应度值已经稳定并达到收敛，表明优化过程稳定，优化结果可靠。表5.3不同方法优化结果由表5.3所示的不同体系可靠度约束优化结果可以看出，体系可靠性优化后结构的重量较常规优化方法的大。......
2023-09-19
-
桥梁可靠度分析方法及应用详细阅读
Rocco等［4］提出了联合SVM和MCS求解结构可靠度的方法。SVM在结构体系可靠度分析中的应用较少。为了发展工程结构体系可靠度理论与方法在桥梁安全评估中的应用，本章将建立桥梁结构体系可靠度分析的简化模型，总结现有结构体系可靠度分析方法，提出基于支持向量机的桥梁结构可靠度分析方法，最后采用两个算例分析表明支持向量机在桥梁结构体系可靠度评估中的应用。......
2023-09-19
-
桥梁可靠度分析的直接抽样法详细阅读
对于通常的实际工程结构，pf为10-3～10-5数量级，若误差小于20%的置信度为95%，则所需模拟次数N＝105～107。一般抽样法的计算量是相当大的，故适用于模拟精度不高的情况。采用该随机数发生器就避免了循环语句的使用，运行时间更短，效率更高。将所有的随机数都计算完后，把结果存储于矩阵中，然后统计矩阵中Y≥0的数量nf，最后由式计算出失效概率，对应于相应的可靠指标。......
2023-09-19
-
桥梁抽样方法分析-桥梁可靠度分析方法与应用详细阅读
一般的MC法用于高度非线性的极限状态曲面或者随机变量维数较高的情况，使用在笛卡儿坐标下的抽样模拟法效率较低，计算耗时较多。因此，Ditlevsen、Olesen、Mohr提出了在标准正态空间中极坐标下进行抽样的方向抽样MC法。③重复步骤①和②直到N次，利用式估计失效概率。对于极限状态曲面接近球面的情况，方向抽样MC法比笛卡尔坐标空间的MC法占较大的优势，若计算接近平面的极限状态曲面时，则无优势。......
2023-09-19
-
可靠指标计算方法-桥梁可靠度分析方法与应用详细阅读
在得出疲劳功能函数和随机变量的概率分布特征之后，可采用一定的可靠度方法计算可靠指标。针对本书已经建立的显式功能函数，其非线性次数较高，若采用传统的一次二阶矩法，则计算出的可靠指标有较大的误差，因此，本书选取了计算精度较高的Monte Carlo抽样方法。可靠指标的计算可采用MATLAB语言编制的“具有显式功能函数的结构可靠度计算软件V1.0”［15］和“复杂结构可靠性分析软件V1.0”［16］等软件进行计算。......
2023-09-19
-
桥梁可靠度分析方法应用：支持向量回归详细阅读
支持向量机是由Vapnik［7］提出的一种机器学习方法，主要有支持向量分类和支持向量回归两种算法。由于SVR是目前结构可靠度分析中的一种较为新颖的方法，下文将简单介绍SVR在结构响应函数拟合应用中的相关理论。SVR学习理论主要是通过如式（3.2）所示的ε敏感函数［8］来控制SVR模型的拟合误差。由式（3.5）可得到SVR模型的函数表达式：为了提高建立SVR模型的效率与精度，可通过对输入样本点及SVR模型参数进行优化。......
2023-09-19
-
桥梁可靠度分析方法—综述与应用详细阅读
把结构可靠度引入到工程结构优化设计数学模型中，根据现有的资源及结构功能要求，选取合适的目标可靠指标为约束条件，并采用遗传算法求解，既可以实现此类工程结构优化设计，又能保证结构在使用过程中的安全性。文献［8］建立了半刚性连接框架的拓扑模型，并结合遗传算法进行了基于体系可靠度的结构优化设计，认为不考虑可靠度的优化设计结构存在安全隐患。......
2023-09-19
相关推荐