桥梁可靠度分析的直接抽样法

2025-09-30 理论教育版权反馈

【摘要】：对于通常的实际工程结构，pf为10-3～10-5数量级，若误差小于20%的置信度为95%，则所需模拟次数N＝105～107。一般抽样法的计算量是相当大的，故适用于模拟精度不高的情况。采用该随机数发生器就避免了循环语句的使用，运行时间更短，效率更高。将所有的随机数都计算完后，把结果存储于矩阵中，然后统计矩阵中Y≥0的数量nf，最后由式计算出失效概率，对应于相应的可靠指标。

设功能函数Z＝g（X）＝g（x1，x2，…，xn）（i＝1，2，…，n）为服从各相应概率密度函数fX（x）的随机变量，按fX（x）对X进行随机抽样，用所得到的样本值x计算功能函数值Z＝g（X），若Z＜0，则模拟中结构失效一次。若共进行了N次模拟，Z＜0出现了nf次，由概率论的大数定律中的Bernoulli定理可知，随机事件Z＜0在N次独立试验中的频率依概率收敛于该事件的概率pf，结构失效概率pf的估计值为：

为减小MonteCarlo法模拟误差，可增加模拟次数，即样本容量N，或采用方差减缩技术，即减缩失效概率估计值的方差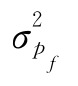 pagenumber_ebook=27,pagenumber_book=17 或变异系数Vpf。对于通常的实际工程结构，pf为10-3～10-5数量级，若误差小于20%的置信度为95%，则所需模拟次数N＝105～107。一般抽样法的计算量是相当大的，故适用于模拟精度不高的情况。

在Matlab语言中，首先用相应随机数发生器（例如正态分布的normrnd）产生随机变量数组xi，然后将产生的所有数据分别替代原结构的参数，进行计算分析。采用该随机数发生器就避免了循环语句的使用，运行时间更短，效率更高。将所有的随机数都计算完后，把结果存储于矩阵中，然后统计矩阵中Y（xi）≥0的数量nf，最后由式（2.17）计算出失效概率，对应于相应的可靠指标。对于工程中常用的参数分布类型的随机数产生命令如下：

产生正态分布随机数：R＝normrnd（mu，sigma，a，b）；

产生对数正态分布随机数：R＝log［lognrnd（mu，sigma，a，b］；

产生极值Ⅰ型分布随机数时，先用均匀分布随机数发生器指令产生一个均布随机变量矩阵，然后用式X＝F-1（r）解出服从极值分布的随机变量矩阵。(https://www.chuimin.cn)

主程序的主要命令如下：

zz＝subs（hanshu，｛bianliang1，bianliang2，bianliang3｝，｛a1，b1，c1｝）；　%功能函数

weizhi＝find（zz＜0）；　%失效的次数的位置

f＿chishu＝length（weizhi）；　%失效的次数

beta＝norminv（1-f＿chishu／canshu∧2）；　%可靠度指标