综上，考虑选择建造的应急服务设施点的数目为6个或7个。由此可知，当算例规模较小时，使用分支定界法得全局最优解计算效率很高。以最大化最小覆盖水平模型求解为例。②目标偏差率最小化模型求解得到的最大偏差率最小，能更好地均衡各个目标。为更好地与分支定界法求解结果进行对比以及分析NSGA-Ⅱ的算法有效性，本节更改设定算法程序中目标个数，分别求解单目标、两目标和三目标模型，并分析求解结果。......
2023-09-19
轴辐网络布局优化模型解析
【摘要】：选中的应急服务设施点的6个地点为马尔康、阿坝、若尔盖、壤塘、茂县和九寨沟与不考虑配送时序特征和仓库容量的布局模型的优化结果有所变动。可见当考虑存在多类需求且各类需求具有明显时序特征时，会对选址结果产生影响。可见，对比不考虑时序特征的布局优化模型，计算规模大大增加，程序运行耗时增长。程序运行超过1小时后依旧未找到全局最优解。
根据各类物资的配送时序特征以及需求量划分多个多层级覆盖临界，其中多功能折叠铲、安全帽属于救援装备类，要求0.5～4小时内送达；医药救护包属于医疗救助类物资，要求2～4小时内送达；帐篷、棉毯属于后勤保障类物资，要求6～10小时内送达。最小覆盖临界分别为：0.5小时、2小时和6小时，最大覆盖临界分别为4小时、4小时、10小时。
表7-14 各地对应急物资的需求量
1）分支定界法求解
（1）P=6时，各模型求解结果（表7-15）
表7-15 P=6时，各模型求解最优目标值
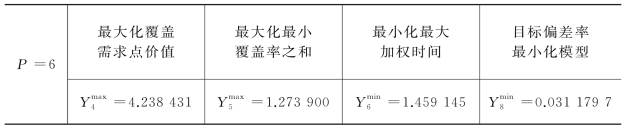
表7-16 P=6时，各模型最大目标值偏差率
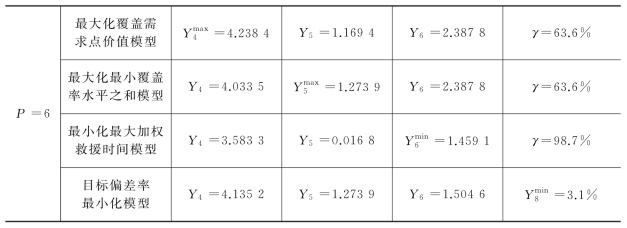
由表7-16可知，四种模型中，目标偏差率最小化模型求解结果得到的最大目标偏差率最小，各个目标值均能获得较好的结果。再次验证了目标偏差率最小化模型能更好均衡兼顾所有分目标。
（2）P=6时，目标偏差率最小化模型的选址结果
表7-17给出了P=6时，目标偏差率最小化模型的选址结果。选中的应急服务设施点的6个地点为马尔康、阿坝、若尔盖、壤塘、茂县和九寨沟与不考虑配送时序特征和仓库容量的布局模型的优化结果有所变动。可见当考虑存在多类需求且各类需求具有明显时序特征时，会对选址结果产生影响。用1、2、3、4、5分别代表折叠铲、安全帽、医药救护包、帐篷、棉毯五种物资，例：马尔康1、2表示马尔康处折叠铲、安全帽需求被覆盖。经计算，13个需求点5种物资的平均覆盖满足水平分别为：折叠铲和安全帽79.1%、医药救护包95.7%、帐篷63.3%、棉毯59.3%。可见当应急服务设施点物资容量有限时，应急物资储备量不足，导致覆盖率水平下降。
表7-17 目标偏差率最小化模型选址结果
（续表）
由表7-17可知，当应急服务设施点储备多类应急物资且考虑配送时序特征及仓库容量限制时，应急服务设施点物资配送服务需求点的路径关系变得复杂，如九寨沟应急服务设施点需覆盖8个需求点的5种不同物资需求。
当配送物资种类和服务关系变得复杂时，对应急服务设施点应急物资储备和配送管理水平要求会显著增高，需提高应急服务设施点应急物资储备和配送管理水平，合理规划物资储备量和物资配送路径关系，否则可能造成应急配送无序、物资浪费、救援效果不理想等后果。
（3）分支定界法的算法有效性
Ⅰ.各模型求解所用时间
表7-18给出了分支定界法的运行时间为37秒，找到全局最优解；分支定界法总共分枝数为7 327个，求解总共迭代次数为510 702次，分枝数和迭代次数均大幅度增加。可见，对比不考虑时序特征的布局优化模型，计算规模大大增加，程序运行耗时增长。
表7-18 P=6时，各模型求解用时（秒）
Ⅱ.P值变化时求解所用时间
以最大化最小覆盖水平之和模型求解为例，统计P值变化时求解用时，如表7-19所示。
表7-19 求解用时
由表7-19可知，P值变化会影响计算求解时间。应急服务设施点选择建造7个时，全局最优解可以找到，分支定界法分枝数为151 260个，程序运行迭代次数为4 646 256次，运行时间为320秒。可见在需求点和设施点均为13个，应急物资种类为5，类别为3的情况下，分支定界法求全局最优解的算法效率有明显下降。
Ⅲ.改变仓库容量限制约束，统计求解所用时间
假设物资堆放高度变为1.8米，再次统计使用分支定界法对各个模型获得全局最优解用时。
表7-20 各模型求解用时（秒）
由表7-20可知，容量限制约束变化会影响求解用时，当物资堆放高度变为为1.8米时，分支定界法求全局最优解的算法效率显著降低。程序运行超过1小时后依旧未找到全局最优解。在3 606秒时强制终止运行，得到的可行解对应目标值为4.481 454。
由此可见，对于大规模的NP-Hard问题，使用精确算法求全局最优解的方式不再适用，本书考虑采用启发式算法——NSGA-Ⅱ算法来求解。
2）NSGA-Ⅱ求解分析
（1）算法求解结果分析
以物资堆放高度变为1.8米时为例，在英特尔CPU：3.30GHZ、matlabR2014a中编程运算，设定：初始种群200，迭代300次，交叉概率0.8，变异概率0.2时，NSGA-Ⅱ算法求解多目标模型，程序运行时长约449秒。运算求解如表7-21所示。
表7-21 P=6时，三目标模型求解目标值
模型求解结果表明，相比使用分支定界法求解目标偏差率最小化模型，NSGA-Ⅱ算法一次运行可得到一组非劣解供决策者选择，以比较不同的决策方案。
（2）NSGA-Ⅱ的算法有效性
Ⅰ.NSGA-Ⅱ求解多目标模型可得到一组非劣解，与全局最优解之间存在一定偏差，但可获得相对较优的可行解。
Ⅱ.改变种群规模和迭代次数，统计算法运算效率。
表7-22 种群规模和迭代次数对计算效率的影响
由表7-22可知，种群规模和迭代次数增加会增大算法程序运行时间，其中种群规模的影响更大。NSGA-Ⅱ算法计算效率较高，程序运行时长可接受。相比分支定界法求全局最优解算法效率优势明显。
综上，在求解较大规模多目标优化NP-Hard问题时，通过两种方法计算求解，总结两种求解方法如下：
一方面，可通过极大模理想点法构建目标偏差率最小化模型，之后采用分支定界法得到全局最优解的方法来求解。当无法得到各目标的最优目标值时，可以对程序运行时间设定一个可接受的上限值，找到相对较优的目标值来代替最优目标值进行求解。
另一方面，相比分支定界法求解目标偏差率最小化模型的方式，多目标遗传算法NSGA-Ⅱ在该情况下呈现出算法效率较高、一次运行可得到多个非劣解、无需事先分别求解得到各分目标的目标值等多个优势，同样可作为一种有效的多目标优化方法。
有关基于轴辐网络的重大突发事件应急设施布局优化理论与应用的文章
- 详细阅读
- 详细阅读
-
基于轴辐网络的应急设施布局详细阅读
应急服务设施轴辐网络具体的优点主要有：1）满足应急物服务的同时需求和多点需求重大突发事件影响范围大，应急服务需求点多，需求次数多。4）扩大应急资源服务的辐射范围轴辐网络上的每一个节点，具有双向性。应急服务设施轴辐网络能够有利于应急枢纽设施的迅速筹集，统计信息准确，避免应急资源积压。......
2023-09-19
-
应急设施布局优化理论与应用-基于轴辐网络的模详细阅读
Campbell提出的MAHSCP模型有n4+n个变量、2n4+n2个约束式，属于复杂的混合整数规划模型，当节点数超过一定数量时，模型求解面临很大问题。翁克瑞[107]根据MAHSCP模型进行了改进，提出了有n2+n个变量、3n2个约束式的新的多分配枢纽覆盖模型。相对Campbell的MAHSCP模型，MAHSCP2模型减少了输入变量，从而以减少问题的输入规模，节约计算内存和时间。......
2023-09-19
-
基于轴辐网络的λ-SASCH模型优化理论详细阅读
重大突发事件下应急服务设施选址轴辐网络布局受到各种因素的影响，而且这种因素具有明显的不确定性，但综合考虑各类因素，实质是对应急服务设施需求的不断变化，即该地区的应急服务设施的重要性不同。......
2023-09-19
-
基于轴辐网络的应急设施布局算法详细阅读
在具有8个节点的轴辐网络中，节点3和节点7是枢纽点，非枢纽点分配给枢纽点的情况见分配序列，节点1分配给枢纽3，其值等于3，节点7是枢纽点，其值等于7。上述比例数据均是从遗传算法参数控制的实际实验中得出。首先按照设定的交叉概率选择“枢纽序列”和“分配序列”各一对，在两序列中随机选取同一交叉点，通过交换交叉点的左右两部分构成新的子代个体。......
2023-09-19
-
基于轴辐网络的突发事件应急设施布局优化方法详细阅读
模糊规划中，用模糊隶属度函数表示约束条件的满足程度、目标函数的期望水平及模型系数的不确定变化范围。概率分布函数未知，不确定性参数使用离散的情景或连续的区间范围来进行描述，其目的是找到一个近似最优解，使它对任意的不确定性参数观测值不敏感。......
2023-09-19
-
轴辐网络布局优化：重大突发事件应急设施布局理详细阅读
轴辐网络布局主要集中于两个问题：枢纽点选址问题和非枢纽点分配问题。对于存在单一隶属关系的公共组织或公共机构网络布局属于单分配的轴辐网络，而复杂的快递物流网络大多采用多分配轴辐网络。轴辐网络结构如图1-1所示。轴辐网络主要应用于快递网络、航线优化布局方面。李阳[51]在其博士论文中将轴辐网络理论应用于救灾物流中，构建了轴辐式救灾物流系统框架，并从救灾物资供应、配送和发放三方面对该系统的功能进行了设计。......
2023-09-19
相关推荐