应急服务设施轴辐网络具体的优点主要有:1)满足应急物服务的同时需求和多点需求重大突发事件影响范围大,应急服务需求点多,需求次数多。4)扩大应急资源服务的辐射范围轴辐网络上的每一个节点,具有双向性。应急服务设施轴辐网络能够有利于应急枢纽设施的迅速筹集,统计信息准确,避免应急资源积压。......
2023-09-19
假设应急服务设施点储备多类应急物资,但不对各类物资时序特征进行详细区分。根据救援紧急程度可知:所有需求均得到满足的最小覆盖临界为0.5小时,所有需求均得不到满足的最大覆盖临界为10小时。
1)分支定界法求解
(1)确定合理的P值
计算分析不同P值对应的目标值,见表7-5。
表7-5 不同P值下的最优目标值
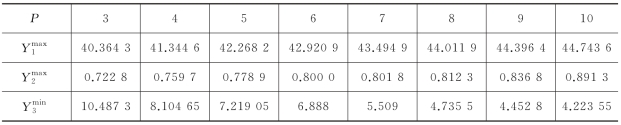
随P值增加覆盖需求点的价值权重变化以及价值权重增幅变化图,分别见图7-4、图7-5。由图表可知:①随着P值增加,覆盖需求点权重和能获得的最大最低覆盖率水平均逐渐增加,而覆盖需求点价值权重增幅逐渐减小。②P为5、8时,覆盖需求点的权重出现较明显的折点,处于折点间的值为6、7。③当P由6、7分别增加为7、8时,覆盖需求点的权重增幅值分别0.574、0.517,增幅值较小。当P为6、7时,能获得的最大最低覆盖率水平分别为0.8、0.801 8,覆盖率水平较高。综上,考虑选择建造的应急服务设施点的数目为6个或7个。
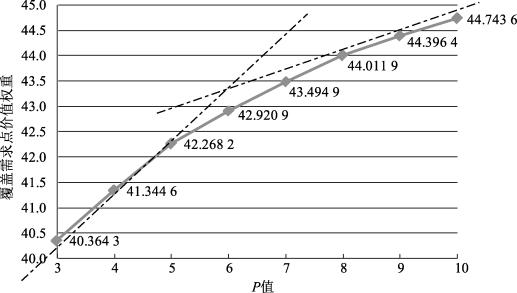
图7-4 覆盖需求点价值权重变化图
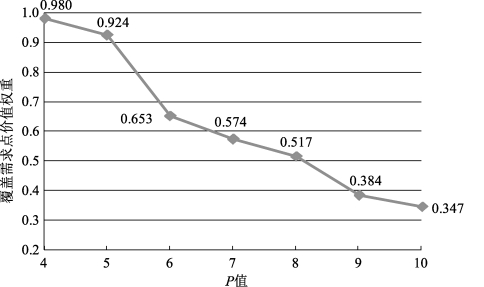
图7-5 覆盖需求点价值权重增幅变化图
(2)P=6时,分析各模型求解的目标值偏差率β(表7-6)
表7-6 P=6时,各模型的最大目标值偏差率

四种模型中,目标偏差率最小化模型求解结果得到的最大目标偏差率最小,各个目标值均能获得较好的结果。说明了目标偏差率最小化模型能更好均衡兼顾所有分目标以及使用该模型进行布局优化的有效性。
(3)P=6时,目标偏差率最小化模型的选址结果
根据表7-7中P=6时,目标偏差率最小化模型的选址结果。选中的建造应急服务设施点的6个地点为小金、阿坝、若尔盖、壤塘、茂县和九寨沟。同时,应急服务设施点与潜在受灾点的依附关系如图7-6所示。
表7-7 P=6时,目标偏差率最小化模型选址结果
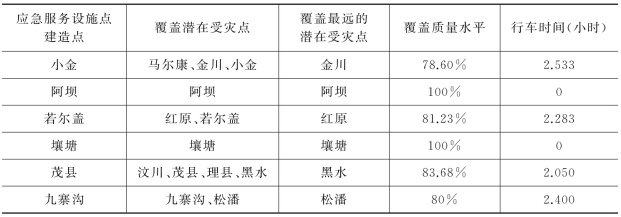
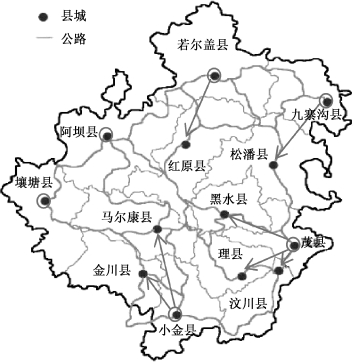
图7-6 应急服务设施点和潜在受灾点间依附关系
注:实际行车路线为曲线,图上线条长短不能直接反映行车距离远近。
(4)分支定界法算法的有效性。
分支定界法的算法有效性体现在两个方面:①解的质量,能否得到全局最优解。②算法效率,算法求解运行时间是否在可接受时长之内。
Ⅰ.阿坝藏族·羌族自治州算例:需求点个数13个,备选应急服务设施点建造点13个。
在英特尔CPU:3.30 GHZ,matlabR2014a中数据和相关参数处理用时0.069 8秒,lingo11中采用分支定界法求解P=6或7情况下的模型用时:![]() 求解时间均不超过1 s,
求解时间均不超过1 s,![]() 求解时间为1 s。由此可知,当算例规模较小时,使用分支定界法得全局最优解计算效率很高。
求解时间为1 s。由此可知,当算例规模较小时,使用分支定界法得全局最优解计算效率很高。
以P=6时程序运行时间为1 s,找到全局最优解,对应目标值为0.8;分支定界法总共分枝数为91个,求解总共迭代次数为138 22次。
Ⅱ.增大算例规模:需求点40个,备选设施点20个。
在400*400的平面内随机生成40个需求点和20个备选设施点坐标(表7-8):
表7-8 需求点和设施点坐标

根据坐标使用欧式距离公式求解需求点到设施点间距离,并由此计算出平均行车时间。设施j到需求点i的平均行车时间=[(Xi-Xj)2+(Yi-Yj)2]1/2/60。以最大化最小覆盖水平模型求解为例。求解用时,如表7-9所示。
表7-9 求解用时

程序运行时间为5秒,找到全局最优解,对应目标值为0.859 263 3;分支定界法总共分枝数为246个,求解总共迭代次数为46 326次,对比算例,分枝数和迭代次数均有增加。根据求解用时可知,当规模增大使用分支定界法获取全局最优解时,计算求解效率依旧较高。
综合(1)~(4)点,一方面说明了模型选址结果的有效性:①最低覆盖质量水平均较高,达到78%以上。②目标偏差率最小化模型求解得到的最大偏差率最小,能更好地均衡各个目标。另一方面说明了使用精确算法-分支定界法求解的有效性:当选址规模增大时,依旧能够得到全局最优解,且程序运行时间较短,算法效率较高。
2)NSGA-Ⅱ求解分析
(1)算法求解结果分析。
为更好地与分支定界法求解结果进行对比以及分析NSGA-Ⅱ的算法有效性,本节更改设定算法程序中目标个数,分别求解单目标、两目标和三目标模型,并分析求解结果。
在英特尔CPU:3.30GHZ,matlabR2014a中编程运算,设定:初始种群100,迭代100次,交叉概率0.8,变异概率0.2。运算结果如表7-10所示。
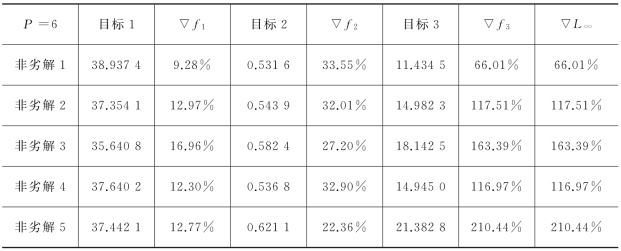
表7-10 P=6时,单目标模型求解目标值和选址结果

这里用∇fi(i=1,2,3)来表示NSGA-Ⅱ算法求解得到的第i个目标值与精确算法求解得到的最优目标值间的偏差率:

当求解多目标时,得到一组非劣解。决策者可以根据偏好,使用不同评判标准从非劣解集中选择最满意的一个可行解。本书以最大目标偏差率(∇L∞)为评判标准来举例评价说明非劣解集中解的优劣:∇L∞越小,认为该非劣解越优。
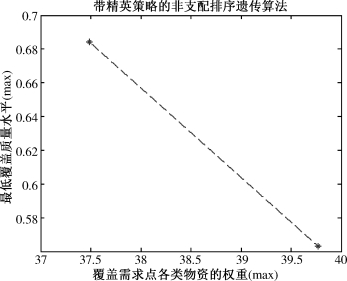
图7-7 双目标(目标1和目标2)模型求解结果
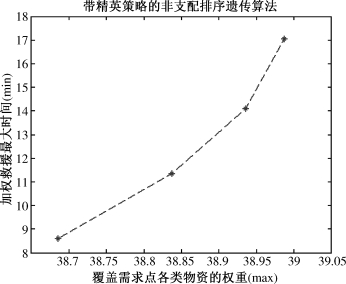
图7-8 双目标(目标1和目标3)模型求解结果
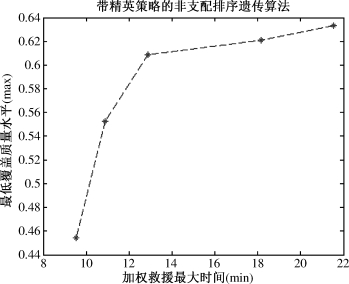
图7-9 双目标(目标2和目标3)模型求解结果
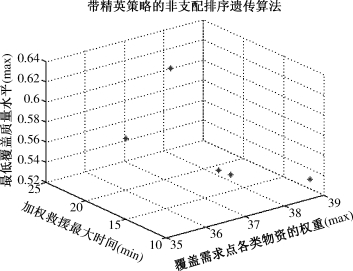
图7-10 三目标模型求解结果
表7-11 P=6时,两目标模型求解目标值

(续表)
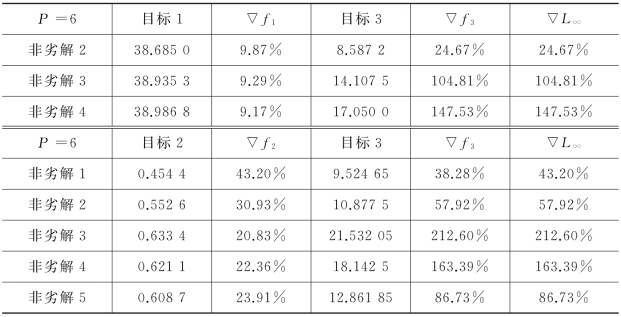
表7-12 P=6时,三目标模型求解目标值
结果分析:
Ⅰ.单目标模型的求解结果表明:NSGA-Ⅱ算法求解单目标模型时,能得到相对较优的可行解,与最优目标值相比偏差率均较小,分别为6.805%、14.475%和24.669%。
Ⅱ.两目标模型的求解结果表明:对于三个目标中的任意两个目标,其中一个变得更优时,另一个目标则变得更差。
Ⅲ.多目标模型求解结果表明:一方面,相比使用分支定界法求解目标偏差率最小化模型,NSGA-Ⅱ算法一次运行可得到一组非劣解供决策者选择,以比较不同的决策方案;且无需事先分别求解得到各分目标的目标值,简化计算步骤;另一方面,NSGA-Ⅱ算法求解多目标模型,目标3的目标偏差率较高,更能兼顾前两个目标。
(2)NSGA-Ⅱ的算法有效性
NSGA-Ⅱ算法的有效性由解的质量、非劣解集中解的数目、算法效率等多个方面综合体现。
Ⅰ.由上述(1)中求解结果分析可知,NSGA-Ⅱ求解多目标模型可得到一组非劣解,该解集中的非劣解是相对较优的可行解,与全局最优解之间存在一定偏差。
Ⅱ.初始种群100,迭代100次,交叉概率0.8,变异概率0.2时,NSGA-Ⅱ算法求解多目标模型,程序运行时长为29秒。改变种群规模和迭代次数,统计算法运算效率。
表7-13 种群规模和迭代次数对计算效率的影响
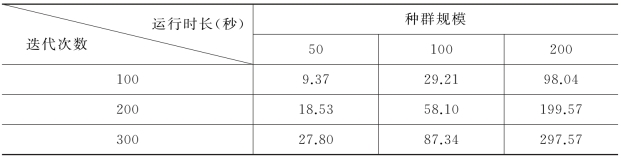
由表7-13可知,种群规模和迭代次数增加会增大算法程序运行时间,其中种群规模的影响更大。NSGA-Ⅱ算法计算效率较高,程序运行时长可接受。但相比分支定界法,该算法并未体现效率优势。
综上,在求解不考虑时序特征和仓库容量的多目标模型时,与NSGA-Ⅱ算法相比,通过极大模理想点法构建目标偏差率最小化模型,之后采用分支定界法得到全局最优解的方法,是一种较为有效的多目标优化方法,能够得到更优质的解,且算法效率更高。
有关基于轴辐网络的重大突发事件应急设施布局优化理论与应用的文章

应急服务设施轴辐网络具体的优点主要有:1)满足应急物服务的同时需求和多点需求重大突发事件影响范围大,应急服务需求点多,需求次数多。4)扩大应急资源服务的辐射范围轴辐网络上的每一个节点,具有双向性。应急服务设施轴辐网络能够有利于应急枢纽设施的迅速筹集,统计信息准确,避免应急资源积压。......
2023-09-19

在具有8个节点的轴辐网络中,节点3和节点7是枢纽点,非枢纽点分配给枢纽点的情况见分配序列,节点1分配给枢纽3,其值等于3,节点7是枢纽点,其值等于7。上述比例数据均是从遗传算法参数控制的实际实验中得出。首先按照设定的交叉概率选择“枢纽序列”和“分配序列”各一对,在两序列中随机选取同一交叉点,通过交换交叉点的左右两部分构成新的子代个体。......
2023-09-19

Campbell提出的MAHSCP模型有n4+n个变量、2n4+n2个约束式,属于复杂的混合整数规划模型,当节点数超过一定数量时,模型求解面临很大问题。翁克瑞[107]根据MAHSCP模型进行了改进,提出了有n2+n个变量、3n2个约束式的新的多分配枢纽覆盖模型。相对Campbell的MAHSCP模型,MAHSCP2模型减少了输入变量,从而以减少问题的输入规模,节约计算内存和时间。......
2023-09-19

模糊规划中,用模糊隶属度函数表示约束条件的满足程度、目标函数的期望水平及模型系数的不确定变化范围。概率分布函数未知,不确定性参数使用离散的情景或连续的区间范围来进行描述,其目的是找到一个近似最优解,使它对任意的不确定性参数观测值不敏感。......
2023-09-19

对于γ-MAHSCP模型,仍属于NP-Hard问题,可采用启发式算法进行模型求解。本书采用分散搜索算法进行求解,分散搜索算法是一种进化算法,依靠类似遗传算法的进化机制,通过迭代向最优解收敛。通过上述分散搜索算法,能够很好地求解γ-MAHSCP模型。该模型得出的结果与γ-SHSCP模型求解不同,因为非枢纽点的分配方式不同,枢纽点的布局也不尽相同。......
2023-09-19

所以,设γ为绕道系数,指每条经过枢纽站的O-D流所需总时间与两点之间直通时间的比值:。即:rk Xik+αtkm Xik Xjm+tjm Xjm≤γ*tiji,j,k,m∈N在第5章L-SHSCP模型的基础上,构建了带有绕道限制的应急服务设施枢纽单分配集覆盖模型:上述变量和约束条件意义同第4章规定,其中约束条件式(5-8)保证所有O-D流的出行时间必须保证在最大绕道系数之内。......
2023-09-19

p-中心选址模型是Hakimi[17]提出的,该模型的目标是为p个服务设施进行选址,使得各个需求点到p个服务设施之间的总加权距离最小。这些应急服务设施,应急响应的及时性要求不是很高。在各类突发事件中,应急服务设施选址涉及经济、技术、社会、安全等诸多因素。魏汝营[35]等综合考虑应急设施选址的效率性、公平性和成本等多方面因素,建立了一个多目标决策模型,采用线性加权和法求解该模型。......
2023-09-19
相关推荐