在具有8个节点的轴辐网络中，节点3和节点7是枢纽点，非枢纽点分配给枢纽点的情况见分配序列，节点1分配给枢纽3，其值等于3，节点7是枢纽点，其值等于7。上述比例数据均是从遗传算法参数控制的实际实验中得出。首先按照设定的交叉概率选择“枢纽序列”和“分配序列”各一对，在两序列中随机选取同一交叉点，通过交换交叉点的左右两部分构成新的子代个体。......
2025-09-30
四川地震带应急设施布局优化分析
【摘要】：四川省是我国地震多发地区，省内分布多个地震带，其中松潘—较场地震带主要分布在民族自治州——阿坝藏族·羌族自治州境内，该地震带内曾发生过数次7级以上地震。最小覆盖临界时间分别为：0.5小时、2小时和6小时，最大覆盖临界时间分别为4小时、4小时、10小时。图7-3阿坝羌族自治州表7-2潜在受灾区之间的平均行车时间（小时）表7-3潜在受灾区地区总人口、面积表7-4应急物资占用储备容量
四川省是我国地震多发地区，省内分布多个地震带，其中松潘—较场地震带主要分布在民族自治州——阿坝藏族·羌族自治州境内，该地震带内曾发生过数次7级以上地震。
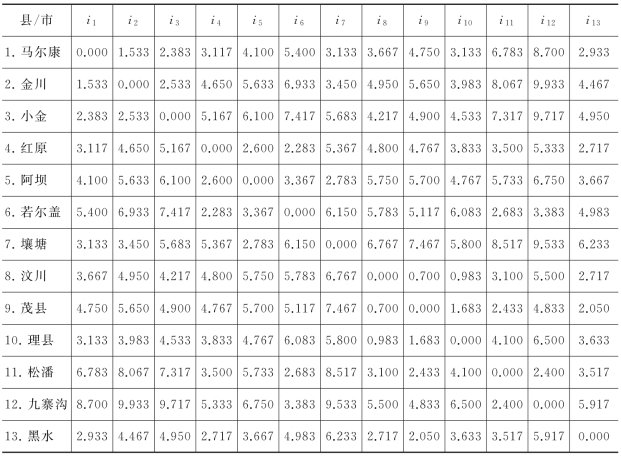
阿坝藏族·羌族自治州位于四川省西北部，地广人稀，辖区内含1市（马尔康市）和12县，如图7-3所示。州政府以其辖区内共13个地区为潜在受灾点，为了应对地震灾害，计划从该13个潜在受灾点中选择合适数目的地点作为应急服务设施点建造地，应急服务设施点的设计基准期为50年；设施点储备的物品包括：多功能折叠铲、安全帽、帐篷、棉毯、医药救护包（主要含说明书、绷带、止血带、创可贴、医用剪刀、镊子、酒精片、纱布片），物资堆放高度为1.5米。应急服务设施点储备的物品及最小、最大临界覆盖时间为：多功能折叠铲、安全帽属于救援装备类，要求0.5～4小时内送达；医药救护包属于医疗救助类物资，要求2～4小时内送达；帐篷、棉毯属于后勤保障类物资，要求6～10小时内送达。最小覆盖临界时间分别为：0.5小时、2小时和6小时，最大覆盖临界时间分别为4小时、4小时、10小时。潜在受灾区之间的距离（公里）参考文献[111]，平均行车速度按照60公里/小时，计算出平均行车时间（小时）见表7-2，各需求区的灾区人口总数（万人）、地区面积（平方千米）见表7-3，应急物资占用储备容量（立方米）见表7-4。i1、i2、…、i13分别为马尔康、金川、小金、红原、阿坝、若尔盖、壤塘、汶川、茂县、理县、松潘、九寨、黑水。
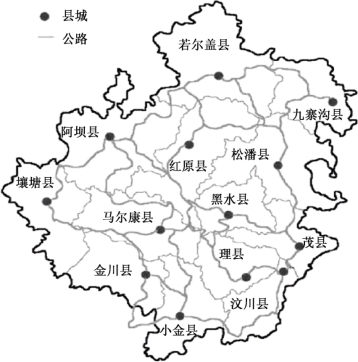
图7-3 阿坝羌族自治州
表7-2 潜在受灾区之间的平均行车时间（小时）
(https://www.chuimin.cn)
表7-3 潜在受灾区地区总人口、面积
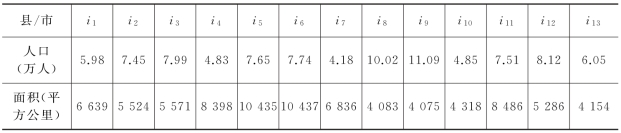
表7-4 应急物资占用储备容量（单位：立方米）
相关文章
- 详细阅读
-
应急设施布局优化理论与应用：原有模型详细阅读
应对大规模应急服务需求的SHSCP模型是在所有网络节点集合中，选择一定数量的节点作为枢纽点，将其余的非枢纽点分配给枢纽点，满足所有约束下，使枢纽数量最少。模型中参数假设如下。例如在应急救援过程中，规定所有的应急救援队伍必须在24小时内到达应急现场并开展救援工作，此时T=24小时。......
2025-09-30
-
基于轴辐网络的应急设施布局详细阅读
应急服务设施轴辐网络具体的优点主要有：1）满足应急物服务的同时需求和多点需求重大突发事件影响范围大，应急服务需求点多，需求次数多。4）扩大应急资源服务的辐射范围轴辐网络上的每一个节点，具有双向性。应急服务设施轴辐网络能够有利于应急枢纽设施的迅速筹集，统计信息准确，避免应急资源积压。......
2025-09-30
-
基于轴辐网络的突发事件应急设施布局优化方法详细阅读
模糊规划中，用模糊隶属度函数表示约束条件的满足程度、目标函数的期望水平及模型系数的不确定变化范围。概率分布函数未知，不确定性参数使用离散的情景或连续的区间范围来进行描述，其目的是找到一个近似最优解，使它对任意的不确定性参数观测值不敏感。......
2025-09-30
-
突发事件应急设施布局优化理论与应用详细阅读
根据突发公共事件的发生过程、性质和机理，突发公共事件主要分为自然灾害、事故灾难、公共卫生事件和社会安全事件四类。根据上述概念的界定，本书中应对重大突发事件的应急服务设施布局是指有效应对各类重大突发事件，提前对永久性的移动类应急服务设施进行规划，确定其数量和位置的过程。......
2025-09-30
-
重大突发事件应急设施布局优化:基于MQCLP详细阅读
，G）中选择5个做应急服务设施点，规定该地区的应急最小临界覆盖距离DL为5公里，最大临界覆盖距离DU为9公里。在此算例中，假设突发事件对应急服务设施的破坏忽视，即psj=1。所以，依据多重数量和质量覆盖模型对应急服务设施进行布局规划，能够解决重大突发事件应急响应过程中需求点多次覆盖和多需求点同时需求的情况，满足不同需求点的不同服务质量水平的要求。表3-2模型输入参数表3-3基于改进遗传算法的模型输出参数......
2025-09-30
-
应急服务设施布局优化理论与应用–解决问题背景详细阅读
应急服务设施为需求点提供服务，即此应急服务设施能够覆盖该需求点。在备用覆盖模型1中，要求每个需求点都必须被服务器覆盖一次的同时，目标是使被覆盖两次的需求点的总价值最大。在实际情况中，可能会因资金预算或政策上的考虑，只能设置固定的P服务器，且某些需求点未能被覆盖到，对此，可使用备用覆盖模型2，该模型是一个双目标优化问题，其目标是将最大化一次覆盖和最大化两次覆盖。应急问题中最显著的特点是强时效性。......
2025-09-30
-
MQCLP模型在重大突发事件应急设施布局优化详细阅读
在覆盖问题研究基础上，构建了满足不同服务质量水平下的多重覆盖模型，即多重数量覆盖和多重质量覆盖模型。解决重大突发事件应急服务设施选址问题，首先根据集合覆盖模型，确定在最大临界距离DU内至少需要的应急设施数量PU。设，根据下列模型求解PU：通过上述模型得出满足基本覆盖要求的设施数量PU，对P与PU进行比较，然后确定利用何种模型。如果P＜PU时，采用最大覆盖模型；当P≥PU时，采用多重数量和质量覆盖模型。......
2025-09-30
相关推荐