对于γ-MAHSCP模型，仍属于NP-Hard问题，可采用启发式算法进行模型求解。本书采用分散搜索算法进行求解，分散搜索算法是一种进化算法，依靠类似遗传算法的进化机制，通过迭代向最优解收敛。通过上述分散搜索算法，能够很好地求解γ-MAHSCP模型。该模型得出的结果与γ-SHSCP模型求解不同，因为非枢纽点的分配方式不同，枢纽点的布局也不尽相同。......
2023-09-19
基于轴辐网络的重大突发事件应急设施布局优化：带有捷径的构建
【摘要】：在应急服务设施轴辐网络中，为了缓解绕道问题，可以增加枢纽个数，但预算则会随之上升，若在有预算约束的条件下，选择在超过绕道系数的O-D流之间建立直通的“捷径”不失为一很好的策略。图5-5当α=0.6、T=1 200、γ*=3时非枢纽点之间的“捷径”分布图5-6当α=0.6、T=1 200、γ*=5时非枢纽点之间的“捷径”分布应急服务设施轴辐网络布局中的绕道问题，通过建立新的枢纽点策略和建立“捷径”通道策略，能够得到很好的解决。
在应急服务设施轴辐网络中，为了缓解绕道问题，可以增加枢纽个数，但预算则会随之上升，若在有预算约束的条件下，选择在超过绕道系数的O-D流之间建立直通的“捷径”不失为一很好的策略。
本节同样以上述算例进行分析和说明，在10个点应急服务设施布局中，以α=0.6、T=1 200时为例，L-SHSCP模型的求解结果是：3（1，2，4，8），9（5，6，7，10）。非枢纽点设施1、2、4和8分配给枢纽点3；非枢纽点设施5、6、7和10分配给枢纽点9，具体的分布见图5-2。
根据
计算每两个节点之间的出行时间：
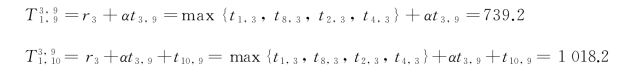
同理，求出所有节点两两之间的出行时间，则网络布局中任意O-D流之间的出行时间如表5-6所示。
表5-6 网络布局中任意O-D流的出行时间（α=0.6，T=1 200）
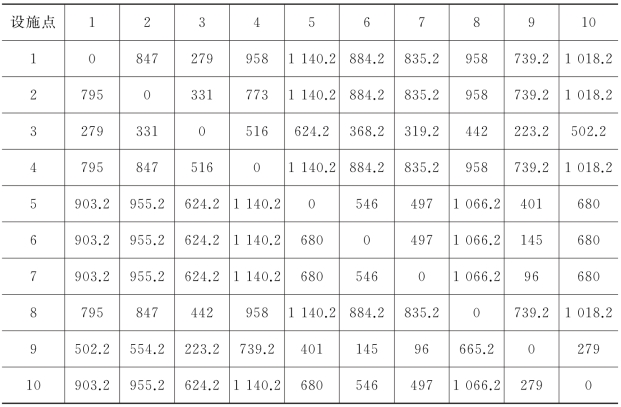
从表5-6可知，最大的出行时间是
，小于1 200，满足最大出行时间约束。当O-D流的始点和终点都分配给一个枢纽时，此时的枢纽半径发生变化，具体值是分配给该枢纽点的所有Spoke，剔除终点后的其余非枢纽点的最大出行时间即为该枢纽的枢纽覆盖半径。例如计算
时，此时的枢纽半径是t1，3，t8，3，t2，3中的最大值，与原来有所差异，因为原来的覆盖半径值由t4，3决定，而此时节点4作为终点，不需要等待其应急服务资源，故此时覆盖半径缩短。
根据绕道系数的定义：
，计算出每条O-D流的绕道系数，具体值见表5-7。
表5-7 网络布局中每条O-D流的绕道系数（α=0.6，T=1 200）
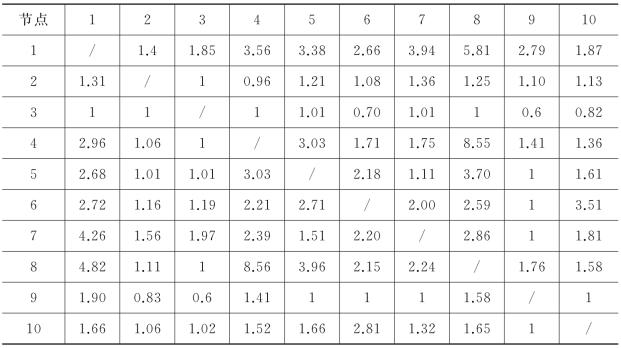
在上述网络布局中，存在着100条O-D流，其中大部分O-D流对的绕道系数都大于1，表示现在的出行时间大于原来的直通时间，而且表中最大值是8.56，说明存在着严重的绕道问题；表中也有部分数值小于1，说明该O-D流的出行时间受到折扣系数α影响较大，这样的O-D流中Hub与Hub之间出行时间占较大比重。同时从表中也可以看出数据矩阵不是对称的，例如γ3，7≠γ7，3，主要是因为始发点不同，各自分配的枢纽点的覆盖半径不同，从而决定了绕道系数不同。
对于“捷径”的建立，主要依据决策者对绕道系数的容忍程度高低或者应急需求点对应急服务的需求缓急而定：如果对绕道问题容忍程度较低或对应急服务需求迫切，则最大绕道系数γ*值较小，网络布局中建立的“捷径”通道也比较多；当容忍程度较高或应急需求点对应急服务的需求不是很急时，最大绕道系数γ*值较大，网络布局中建立的“捷径”通道也比较少。例如，当设定的最大绕道系数γ*值等3时，上述布局网络中要建立12条“捷径”通道，如图5-5中虚线所示；当最大绕道系数γ*值等5时，上述布局网络中要建立3条“捷径”通道，见图5-6中的虚线。当最大绕道系数γ*值大于8.56时，此时等同于释放了绕道约束条件，和无绕道约束的轴辐网络布局相同。
图5-5 当α=0.6、T=1 200、γ*=3时非枢纽点之间的“捷径”分布
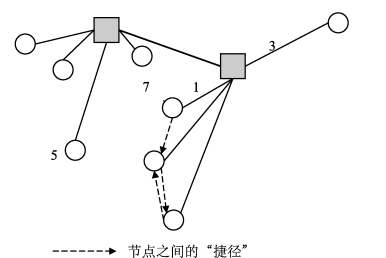
图5-6 当α=0.6、T=1 200、γ*=5时非枢纽点之间的“捷径”分布
应急服务设施轴辐网络布局中的绕道问题，通过建立新的枢纽点策略和建立“捷径”通道策略，能够得到很好的解决。而两种策略各有利弊，例如上述实例α=0.6、T=1 200的情况，绕道系数设定为γ*=3时，如果采用建立新枢纽点策略，则在原枢纽点3、9的基础上增加枢纽点6、8，设施成本上升；如果采用“捷径”通道策略，则在网络中建立12条“捷径”通道，但此时整个轴辐网络的规模效益降低，路线网络复杂，容易造成调度混乱，路线拥堵等问题。所以，具体选择哪种策略，决策者应根据应急情景和成本预算的情况，从而有针对性地选择最有利于应急救援服务的策略。
有关基于轴辐网络的重大突发事件应急设施布局优化理论与应用的文章
- 详细阅读
-
基于轴辐网络的重大突发事件应急设施布局详细阅读
p-中心选址模型是Hakimi[17]提出的，该模型的目标是为p个服务设施进行选址，使得各个需求点到p个服务设施之间的总加权距离最小。这些应急服务设施，应急响应的及时性要求不是很高。在各类突发事件中，应急服务设施选址涉及经济、技术、社会、安全等诸多因素。魏汝营[35]等综合考虑应急设施选址的效率性、公平性和成本等多方面因素，建立了一个多目标决策模型，采用线性加权和法求解该模型。......
2023-09-19
-
基于轴辐网络的重大突发事件应急设施布局问题分详细阅读
在应急服务设施轴辐网络布局构建过程中，核心问题就是枢纽点设施位置和数量以及非枢纽点设施的分配方式的确定，从而规划O-D流路线。在单分配和多分配问题上，即非枢纽点分配给一个枢纽点还是多个枢纽点，考虑到应急服务设施属于公共设施，公共部门管辖，而Hub设施和非枢纽点存在着上下级的行政隶属关系，根据行政管理中的单一领导原则。Campbell[104]对枢纽站最大覆盖问题给出了单分配模型，此类模型具有O个变量与约束条件，具体模型如下。......
2023-09-19
- 详细阅读
-
基于轴辐网络的突发事件应急设施布局优化方法详细阅读
模糊规划中，用模糊隶属度函数表示约束条件的满足程度、目标函数的期望水平及模型系数的不确定变化范围。概率分布函数未知，不确定性参数使用离散的情景或连续的区间范围来进行描述，其目的是找到一个近似最优解，使它对任意的不确定性参数观测值不敏感。......
2023-09-19
-
基于轴辐网络的重大突发事件应急设施布局优化理详细阅读
折扣系数α依次取值为0.4、0.6和0.8；最大时间约束T分别取值720、960、1 200和1 440分钟；γ*分别取3和5。基于第4章设计的改进的遗传算法，通过算例验证将两模型结果进行比较，并对两个模型的不同参数分析对比。......
2023-09-19
-
基于轴辐网络的应急设施布局详细阅读
应急服务设施轴辐网络具体的优点主要有：1）满足应急物服务的同时需求和多点需求重大突发事件影响范围大，应急服务需求点多，需求次数多。4）扩大应急资源服务的辐射范围轴辐网络上的每一个节点，具有双向性。应急服务设施轴辐网络能够有利于应急枢纽设施的迅速筹集，统计信息准确，避免应急资源积压。......
2023-09-19
-
基于轴辐网络的突发事件应急设施布局详细阅读
所以，设γ为绕道系数，指每条经过枢纽站的O-D流所需总时间与两点之间直通时间的比值：。即：rk Xik+αtkm Xik Xjm+tjm Xjm≤γ*tiji，j，k，m∈N在第5章L-SHSCP模型的基础上，构建了带有绕道限制的应急服务设施枢纽单分配集覆盖模型：上述变量和约束条件意义同第4章规定，其中约束条件式（5-8）保证所有O-D流的出行时间必须保证在最大绕道系数之内。......
2023-09-19
相关推荐