轴辐网络布局主要集中于两个问题：枢纽点选址问题和非枢纽点分配问题。对于存在单一隶属关系的公共组织或公共机构网络布局属于单分配的轴辐网络，而复杂的快递物流网络大多采用多分配轴辐网络。轴辐网络结构如图1-1所示。轴辐网络主要应用于快递网络、航线优化布局方面。李阳[51]在其博士论文中将轴辐网络理论应用于救灾物流中，构建了轴辐式救灾物流系统框架，并从救灾物资供应、配送和发放三方面对该系统的功能进行了设计。......
2023-09-19
基于轴辐网络的重大突发事件应急设施布局优化理论与应用
【摘要】：折扣系数α依次取值为0.4、0.6和0.8；最大时间约束T分别取值720、960、1 200和1 440分钟；γ*分别取3和5。基于第4章设计的改进的遗传算法，通过算例验证将两模型结果进行比较，并对两个模型的不同参数分析对比。
为了验证带有绕道限制的枢纽选址分配模型的正确性，同时也为了和第4章构建的无绕道约束的模型进行对比，本算例依然应用第4章数据来进行验证，为了便于计算，选取表4-1中前10个点的数据，如表5-1所示，与之相应，前10个应急服务设施的权重如表5-2所示。
表5-1 10个应急服务设施之间的出行时间（分钟）
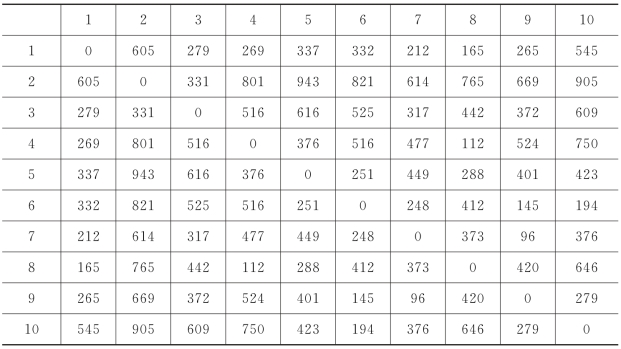
表5-2 10个应急服务设施的候选权重
算法涉及的相关参数设定如下：种群规模为100，最大遗传代数max GEN为200，交叉概率为0.6，变异概率为0.1，GEN_C等于80，ε=0.001。基于上述参数，利用算法对γ-SHSCP模型在电脑上（配置）进行计算。折扣系数α依次取值为0.4、0.6和0.8；最大时间约束T分别取值720、960、1 200和1 440分钟；γ*分别取3和5。模型的求解结果如表5-3和表5-4所示。
表5-3 改进遗传算法对γ-SHSCP模型求解结果（γ*=3）
（续表）
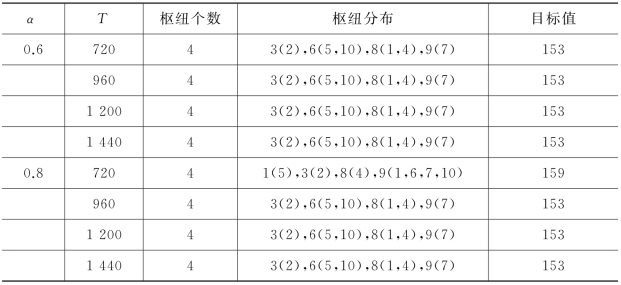
表5-4 改进遗传算法对γ-SHSCP模型求解结果（γ*=5）
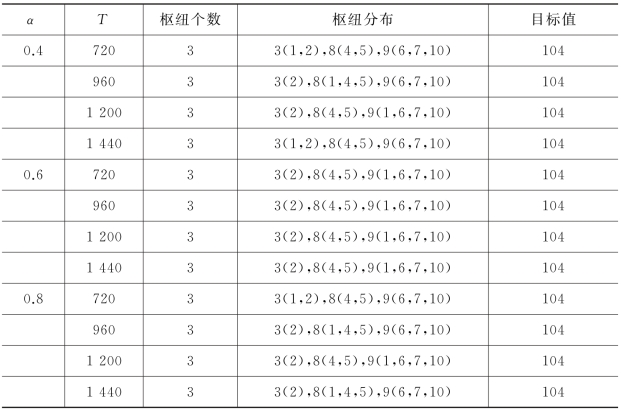
从有绕道约束的γ-SHSCP模型求解结果（表5-3、表5-4）可以看出，具有相同T和α约束下，γ-SHSCP模型中的枢纽数量均大于第4章L-SHSCP模型（表4-3）中的枢纽数量。在γ-SHSCP模型中，枢纽点的数量随着最大时间约束T值的变化而未发生改变；观察折扣系数α变化可知，当γ*=3时，α从0.6增加到0.8后，虽然枢纽数量没有改变，但目标函数增大，说明随着折扣系数的增大，原来适合作为枢纽点的节点已不能满足要求，只能寻求其他的重要程度较低的节点作为枢纽点，使得目标值增大。只有当绕道系数γ*不断增大（从3增大到5）时，枢纽数量才逐渐减少，非枢纽节点的分配情况也随之发生改变，这说明此时绕道系数γ*约束强于T和α的约束，有、无“绕道”约束的轴辐网络布局对比情况如图5-2、图5-3所示。
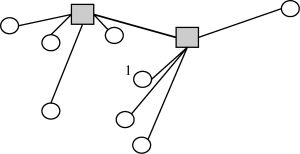
图5-2 α=0.6、T=1 200时无绕道系数限制轴辐网络
图5-3 α=0.6、T=1 200、γ*=3时有绕道约束的轴辐网络
同时，为了检验绕道系数的约束能力，逐渐增大γ*值，具体求解结果如表5-5所示，表中给出了当α=0.8、T=1 440时，枢纽数量随绕道系数γ*变化的不同结果。从表5-5可以看出，绕道系数越大，枢纽数量越少，当γ*=15时，γ-SHSCP模型中的绕道约束能力可以视为0，等于释放“绕道”约束，此时模型等同于L-SHSCP。在此算例中，由于算例的数据变化较大，其中两点之间的直接出行时间最大值t25=943，最小值t79=96，造成直接出行时间与通过枢纽出行的时间比值具有很大的区间，故本算例中的γ*取值也较大，而且起主要约束作用。
表5-5 当α=0.8、T=1 440时随绕道系数变化求解结果
对于上述两模型中的参数组合的每种情况，都进行了20次计算，一般情况都能得到最优解，算法的搜索效果不错，同时根据改进遗传算法的收敛情况（图5-4），种群适应度逐渐向最优适应度值收敛，收敛速度和计算结果令人满意，也说明改进遗传算法对两类模型求解的有效性。
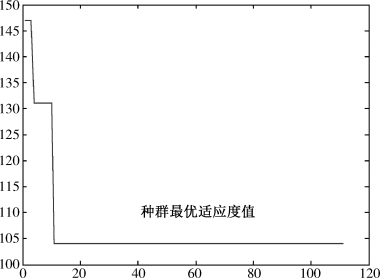
图5-4 改进遗传算法的收敛性（α=0.8，T=1 200，γ*=5）
本节考虑了轴辐网络的绕道缺点，对L-SHSCP模型进行了扩展，提出带有绕道约束的应急服务设施单分配集覆盖选址-分配模型（γ-SHSCP）。基于第4章设计的改进的遗传算法，通过算例验证将两模型结果进行比较，并对两个模型的不同参数分析对比。研究结果表明：绕道系数具有很强的约束力，枢纽数量变化程度要明显强于T和α的影响，也即说明在应急服务设施轴辐网络中绕道问题是很明显的问题。调整绕道系数后结果会有较大的变动，这就需要根据具体应急服务需求的急缓和具体道路情况来确定具体绕道系数的大小，从而确定轴辐网络中的枢纽位置和非枢纽点的分配。所以，构建带有绕道约束的模型，增加枢纽点，是解决轴辐网络中绕道问题的一个有效策略。但该策略在预算限定的情况下则不太适应，由于增加枢纽点，预算上升，如果对于经济能力有限的情况，可以寻求第二种策略，即轴辐网络“捷径”策略。
有关基于轴辐网络的重大突发事件应急设施布局优化理论与应用的文章
- 详细阅读
-
基于轴辐网络的重大突发事件应急设施布局优化算详细阅读
对于γ-MAHSCP模型，仍属于NP-Hard问题，可采用启发式算法进行模型求解。本书采用分散搜索算法进行求解，分散搜索算法是一种进化算法，依靠类似遗传算法的进化机制，通过迭代向最优解收敛。通过上述分散搜索算法，能够很好地求解γ-MAHSCP模型。该模型得出的结果与γ-SHSCP模型求解不同，因为非枢纽点的分配方式不同，枢纽点的布局也不尽相同。......
2023-09-19
-
基于轴辐网络的重大突发事件应急设施布局详细阅读
p-中心选址模型是Hakimi[17]提出的，该模型的目标是为p个服务设施进行选址，使得各个需求点到p个服务设施之间的总加权距离最小。这些应急服务设施，应急响应的及时性要求不是很高。在各类突发事件中，应急服务设施选址涉及经济、技术、社会、安全等诸多因素。魏汝营[35]等综合考虑应急设施选址的效率性、公平性和成本等多方面因素，建立了一个多目标决策模型，采用线性加权和法求解该模型。......
2023-09-19
- 详细阅读
-
基于轴辐网络的重大突发事件应急设施布局问题分详细阅读
在应急服务设施轴辐网络布局构建过程中，核心问题就是枢纽点设施位置和数量以及非枢纽点设施的分配方式的确定，从而规划O-D流路线。在单分配和多分配问题上，即非枢纽点分配给一个枢纽点还是多个枢纽点，考虑到应急服务设施属于公共设施，公共部门管辖，而Hub设施和非枢纽点存在着上下级的行政隶属关系，根据行政管理中的单一领导原则。Campbell[104]对枢纽站最大覆盖问题给出了单分配模型，此类模型具有O个变量与约束条件，具体模型如下。......
2023-09-19
-
基于轴辐网络的应急设施布局详细阅读
应急服务设施轴辐网络具体的优点主要有：1）满足应急物服务的同时需求和多点需求重大突发事件影响范围大，应急服务需求点多，需求次数多。4）扩大应急资源服务的辐射范围轴辐网络上的每一个节点，具有双向性。应急服务设施轴辐网络能够有利于应急枢纽设施的迅速筹集，统计信息准确，避免应急资源积压。......
2023-09-19
-
基于轴辐网络的突发事件应急设施布局优化方法详细阅读
模糊规划中，用模糊隶属度函数表示约束条件的满足程度、目标函数的期望水平及模型系数的不确定变化范围。概率分布函数未知，不确定性参数使用离散的情景或连续的区间范围来进行描述，其目的是找到一个近似最优解，使它对任意的不确定性参数观测值不敏感。......
2023-09-19
-
基于轴辐网络的突发事件应急设施布局详细阅读
所以，设γ为绕道系数，指每条经过枢纽站的O-D流所需总时间与两点之间直通时间的比值：。即：rk Xik+αtkm Xik Xjm+tjm Xjm≤γ*tiji，j，k，m∈N在第5章L-SHSCP模型的基础上，构建了带有绕道限制的应急服务设施枢纽单分配集覆盖模型：上述变量和约束条件意义同第4章规定，其中约束条件式（5-8）保证所有O-D流的出行时间必须保证在最大绕道系数之内。......
2023-09-19
相关推荐