由此可得动能和化学能共同作用下的开孔孔径dc图6.35活性聚能侵彻体作用混凝土靶开孔效应2.内爆超压模型活性聚能侵彻体贯穿混凝土靶后，在目标内部发生剧烈爆燃反应，形成超压场。图6.37靶后1 m处内爆超压时程曲线图6.38靶后2 m处内爆超压时程曲线活性聚能侵彻体等效TNT当量为100 g时，不同爆心位置处，靶后1 m和2 m处超压时程曲线分别如图6.39和图6.40所示。图6.41靶后超压时程曲线......
2025-09-29
L-SHSCP模型实际应用分析
【摘要】：基于上述参数的算法，分别对L-SHSCP模型在电脑（配置）上进行计算。对L-SHSCP模型，折扣系数α依次取值为0.4、0.6和0.8；最大时间约束T分别取值720、960、1 200和1 440分钟。根据改进遗传算法的收敛情况，种群适应度逐渐向最优适应度值收敛，收敛速度和计算结果令人满意，也说明改进遗传算法对L-SHSCP模型求解的有效性。
本算例主要是验证模型与算法的有效性。某地区有20个应急服务设施点，各设施之间的最短出行时间及各点的位置布局如表4-1和图4-4所示。规定在20个应急服务设施中选择一定数量的设施作为枢纽点，在满足规定的最大达到时间约束下，覆盖所有的设施点。
表4-1 20个应急服务设施之间的出行时间（分钟）
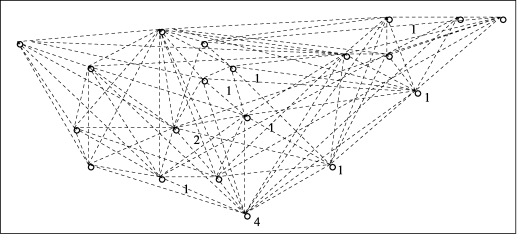
图4-4 算例中20个应急设施点布局位置
根据每个设施点的地理状况、覆盖人口、交通运输能力等情况，通过事先确定的应急服务设施评价指标体系，对每个候选枢纽点的重要程度进行综合打分，即获得各候选设施点的重要性权重。见表4-2，其中表述数据越小，则权重越小，越容易被选中成为枢纽点。
表4-2 20个应急服务设施的权重
（注：表中的数据，假设权重最大取100，最小为0，权重量纲大小与模型求解无影响，只需区分各点作为候选点的优劣程度即可。）
将上述改进遗传算法编译成Matlab程序，在Matlab R2008a中对LSHSCP模型进行数值试验，算法涉及的相关参数设定如下：种群规模为100，最大遗传代数max GEN为200，交叉概率为0.6，变异概率为0.1，GEN_C等于50，ε=0.001。基于上述参数的算法，分别对L-SHSCP模型在电脑（配置）上进行计算。对L-SHSCP模型，折扣系数α依次取值为0.4、0.6和0.8；最大时间约束T分别取值720、960、1 200和1 440分钟。为了验证模型中的解随数据规模变化的情况，分别对算例中候选设施点数量N=10、N=15、N=20三种情况进行求解，来验证模型的有效性和分析各参数的变化情况，模型的求解结果如表4-3、表4-4所示。
通过改进的遗传算法对算例进行求解，从结果可以看出，当T不变，时间折扣系数α从0.4增加到0.6、0.8时，目标函数值不断增大（如表4-4、表4-5所示，由于表4-3数据规模较小，趋势不明显）。例如当n=15，T=720时，目标值从原来的104增加到136，说明随着枢纽与枢纽之间的运行时间折扣不明显，经过枢纽点O-D流的出行时间增加，使得有些流线不满足T的约束，枢纽点位置发生变化，原来适合做枢纽点的设施点已经不能满足要求，只能寻求重要程度次之的设施点，使得目标值上升。同时布局发生改变，由于折扣系数α影响不是特别大，所以，枢纽数量没有发生改变，即都是3个。
表4-3 n=10时模型求解结果
表4-4 n=15时模型求解结果
(https://www.chuimin.cn)
（续表）
表4-5 n=20时模型求解结果
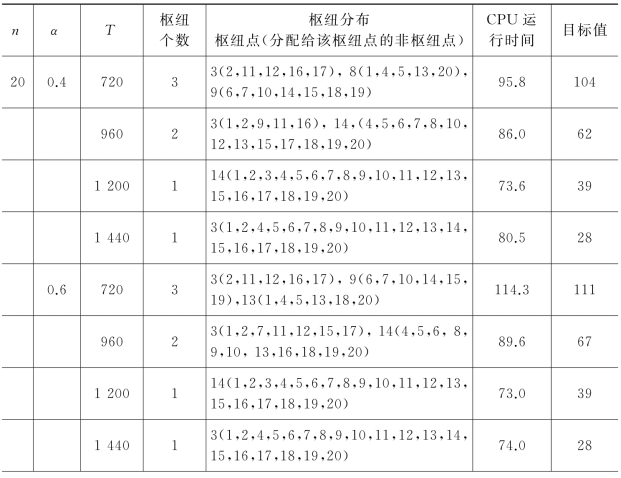
（续表）
当α不变，最大时间约束T从原来的720逐渐增加到1 440，目标值不断减小，枢纽数量也随之减小，原因是随着T的增大，最大时间约束不断得到释放，使得原来受T约束的路线已经满足要求，枢纽数量也会随之减少。通过上述表中数据对比，发现目标值的变化随T的变化要比α的变化要大，说明T的约束强于α。综合T和α的变化，枢纽布局和非枢纽点的分配也发生很大变化，图4-5和图4-6给出了两种布局变化情况。
图4-5 当n=20，α=0.4，T=720应急服务设施轴辐网络布局
对于上述各参数的每种组合情况，分别进行了20次计算，一般情况都能得到最优解，算法的搜索效果不错。其中，表中的CPU运行时间是由20次的运行时间平均得出，从表4-3～表4-5可以看出，随着n的数量的增大，运行时间迅速增大，但都在可接受的范围内。根据改进遗传算法的收敛情况（图4-7），种群适应度逐渐向最优适应度值收敛，收敛速度和计算结果令人满意，也说明改进遗传算法对L-SHSCP模型求解的有效性。
图4-6 当n=20，α=0.8，T=960时应急服务设施轴辐网络布局
图4-7 算法的收敛性（n=20，α=0.8，T=960）
相关文章
- 详细阅读
-
浸渍钎焊技术在实际应用中的案例分析详细阅读
为了保证焊接质量，钎焊前需要仔细清洗焊件，目的是把焊件表面的油渍及厚氧化膜去除。预热温度为500～540℃，保温2～5min。盐浴钎焊时应尽可能保证密闭通道内空气排出，防止空气被封闭在空腔内阻碍熔盐润湿所有待钎表面。氟化物钎剂在钎焊过程中依靠溶胀作用使氧化膜强度下降，同时氧化剂的存在降低了金属的表面张力使钎料易于铺展。熔盐准备过程中，要保证熔盐的pH值为5.3～7.0。如果pH值超过7.0，则需AF添加剂调节。......
2025-09-29
-
实际应用重要，理论构建不可忽视详细阅读
与西方国家的科学技术相比，中国传统科学技术一开始便具有鲜明的实用性取向。所以，尽管中国古代的科学家们在天文学方面拥有丰富的观测资料，但是却只是为制定历法服务，极少尝试理论构建，自然也就未能形成系统的理论体系。......
2025-09-30
-
实际洪水法应用于水文分析计算与水资源评价详细阅读
实际洪水法是指通过实际洪水调查能弄清楚洪泛区的淹没面积和水位，从而进行洪水风险分析与制图。图11.31954年长江中下游洪水淹没范围利用实际洪水法主要从近年来袭击流域的洪水中挑选一二次具有重大灾害的洪水进行研究。至于流量记录，它指流经包括河槽和洪泛区在内的测量断面的所有水流的流量。这也是图11.3一直作为长江中下游防洪规划依据之一的重要原因。图11.4水文学和水力学法的流程......
2025-09-30
-
C@T蒸发产电装置实际应用情况分析详细阅读
蒸发产电装置的串并联集成如图4.75所示。考虑到以C@T材料为主体的蒸发产电器件具有良好的光响应性，将其应用于自供电光控开关。在太阳光照下蒸发产电装置的FIV将迅速降低至零，得到的电信号经放大器放大后传递到继电器上，促使继电器进行相应响应，触发电路断路，导致灯泡处于“关闭”状态。......
2025-09-29
-
TensorFlow模型介绍与应用详细阅读
TensorFlow支持通过tf.graph（）函数来生成新的计算图。有效地整理TensorFlow中的资源同样也是计算图的重要功能之一。在TensorFlow程序中，所有数据都可以通过张量的形式来表示。每一个张量都有一个唯一的张量类型，在对张量进行运算前，TensorFlow首先会对张量进行类型检查，当发现类型不匹配时就会保存。运行模型会话是拥有并管理TensorFlow程序运行时所有资源的概念，是TensorFlow的运行模型。......
2025-09-29
-
实际应用：IGN阵列纳米发电机详细阅读
在弄清楚以上影响IGN阵列纳米发电机湿气产电的条件之后，继续开展在一定条件下不同价态IGN湿气产电稳定性能的研究工作，以证明其有潜力在人类未来生活中发挥实际应用价值。最后，对AlGN阵列纳米发电机进行测试。这都说明了本节中所设计的利用湿气能量转换为电能的基于高价载流子迁移的IGN阵列纳米发电机具有很有光明的实用前景。......
2025-09-29
-
变频器在实际应用中的作用及应用案例详细阅读
可编程序控制器、变频器、伺服电机、人机界面是驱动控制系统中不可缺少的组成部分。通常，纺织机械系统中的电动机普遍采用通用变频器控制，所有的变频器则统一由PLC控制。图解演示例如，图11-35所示变频器在电梯智能控制中的应用。图11-35 变频器在电梯智能控制中的应用5.变频器在民用改善环境中的应用随着人们对生活质量和环境的要求不断提高......
2025-09-29
相关推荐