轴辐网络布局主要集中于两个问题：枢纽点选址问题和非枢纽点分配问题。对于存在单一隶属关系的公共组织或公共机构网络布局属于单分配的轴辐网络，而复杂的快递物流网络大多采用多分配轴辐网络。轴辐网络结构如图1-1所示。轴辐网络主要应用于快递网络、航线优化布局方面。李阳[51]在其博士论文中将轴辐网络理论应用于救灾物流中，构建了轴辐式救灾物流系统框架，并从救灾物资供应、配送和发放三方面对该系统的功能进行了设计。......
2025-09-30
重大突发事件应急设施布局优化:基于MQCLP模型的应用
【摘要】：，G）中选择5个做应急服务设施点，规定该地区的应急最小临界覆盖距离DL为5公里，最大临界覆盖距离DU为9公里。在此算例中，假设突发事件对应急服务设施的破坏忽视，即psj=1。所以，依据多重数量和质量覆盖模型对应急服务设施进行布局规划，能够解决重大突发事件应急响应过程中需求点多次覆盖和多需求点同时需求的情况，满足不同需求点的不同服务质量水平的要求。表3-2模型输入参数表3-3基于改进遗传算法的模型输出参数
某地区有10个社区（1～10），当地政府计划在7个候选设施地址（A，B，…，G）中选择5个做应急服务设施点，规定该地区的应急最小临界覆盖距离DL为5公里，最大临界覆盖距离DU为9公里。假定每个街区的需求都集中在社区中心，7个候选设施到10个社区中心的行车距离dij（公里）及10个社区的人口数量（千人）如表3-1所示。
表3-1 候选设施到各社区的行车距离和社区人口数量
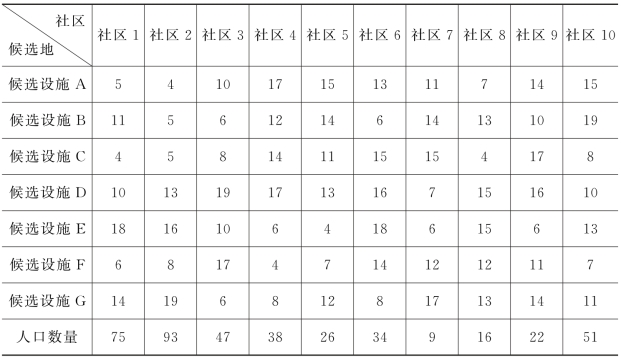
在此例中，假设应急情景已知，并且有所防备。当地政府根据人口分布情况、突发事件发生的概率和突发事件对该社区的影响程度，基于每个社区的需求权重βis×eis×Mi，确定了每个社区至少需要的设施数量，如表3-2所示。具有大权重的需求点表示此点的脆弱性较大，需要更多的应急设施。例如，社区2的权重比较大，对于其他点比较而言，此点需要更多的设施。
在此算例中，假设突发事件对应急服务设施的破坏忽视，即psj=1。根据模型式（3-12）～式（3-14），当最大临界距离DU等于9公里时，至少需要3个应急服务设施。本算例中确定的P=5个应急服务设施，采用多重数量和质量覆盖模型进行布局优化。
基于算例的输入参数，利用构建的多重数量和质量覆盖模型，来确定算例中应急服务设施的布局。用Matlab7.6.0（R2008a）软件按照上述改进遗传算法编程计算此模型，其中染色体群体规模定为100，交叉率为35%，突变率为5%，模型输出结果如表3-3所示。(https://www.chuimin.cn)
结果显示：设施点应该选择在B、C、E、F、G，且结果是合理的，因为所有需求点的覆盖次数均被满足，而且具有大权重的需求点如社区1、社区2和社区3被多次覆盖，覆盖水平为1，或接近于1；社区3要求被覆盖次数为2，而实际达到了覆盖3次。满足数量和质量要求的服务设施所覆盖的人口比例达到整体人口的91.65%，这也说明此模型是非常有效的。若是采用传统的最大覆盖模型得出的解包括（A、C、E、F、G），此解同样满足初始对覆盖次数的要求，但对于社区3只能覆盖2次，覆盖水平为0.81；社区6的覆盖次数为1，覆盖水平为0.13，覆盖人口比例是81.79%，此解劣于多重数量和质量覆盖模型所求的解。所以，依据多重数量和质量覆盖模型（MQCLP）对应急服务设施进行布局规划，能够解决重大突发事件应急响应过程中需求点多次覆盖和多需求点同时需求的情况，满足不同需求点的不同服务质量水平的要求。
表3-2 模型输入参数
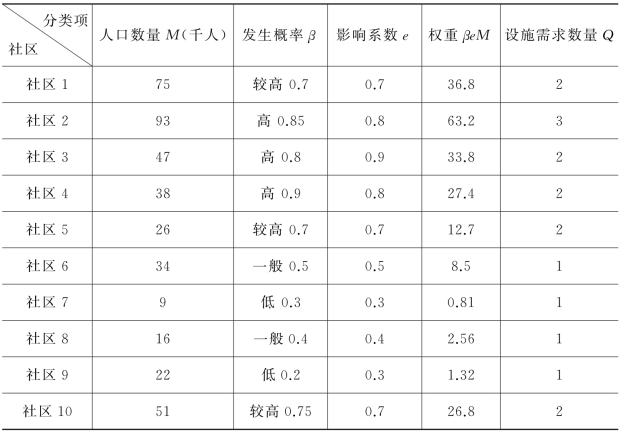
表3-3 基于改进遗传算法的模型输出参数
相关文章
- 详细阅读
-
基于轴辐网络的重大突发事件应急设施布局详细阅读
p-中心选址模型是Hakimi[17]提出的，该模型的目标是为p个服务设施进行选址，使得各个需求点到p个服务设施之间的总加权距离最小。这些应急服务设施，应急响应的及时性要求不是很高。在各类突发事件中，应急服务设施选址涉及经济、技术、社会、安全等诸多因素。魏汝营[35]等综合考虑应急设施选址的效率性、公平性和成本等多方面因素，建立了一个多目标决策模型，采用线性加权和法求解该模型。......
2025-09-30
-
突发事件应急设施布局优化理论与应用详细阅读
根据突发公共事件的发生过程、性质和机理，突发公共事件主要分为自然灾害、事故灾难、公共卫生事件和社会安全事件四类。根据上述概念的界定，本书中应对重大突发事件的应急服务设施布局是指有效应对各类重大突发事件，提前对永久性的移动类应急服务设施进行规划，确定其数量和位置的过程。......
2025-09-30
-
重大突发事件下的应急服务设施轴辐网络布局优化详细阅读
第2章研究了重大突发事件下的应急服务需求的特点，在此基础上提出了应急服务设施轴辐网络布局框架，并对轴辐网络的运行和相关保障措施进行了研究。针对这两类问题，分别给出了两种不同的策略。第8章对全书内容及研究结论进行总结，并对书中有待进一步深入研究的地方提出后续研究的方向。......
2025-09-30
-
基于轴辐网络的应急设施布局详细阅读
应急服务设施轴辐网络具体的优点主要有：1）满足应急物服务的同时需求和多点需求重大突发事件影响范围大，应急服务需求点多，需求次数多。4）扩大应急资源服务的辐射范围轴辐网络上的每一个节点，具有双向性。应急服务设施轴辐网络能够有利于应急枢纽设施的迅速筹集，统计信息准确，避免应急资源积压。......
2025-09-30
-
基于轴辐网络的应急设施布局在实践中的应用详细阅读
而关于应急领域的轴辐网络布局更注重时效性，轴辐网络应用在应急领域，主要体现在规模经济性、网络协同性和联动性等方面。本书对城际多Hub应急物流网络的协同性进行研究，并说明该网络能够有效控制生物危险源的扩散，提高应急系统在多个城市之间的应急管理水平。轴辐网络在国外被成功应用于应急救援、应急物流等领域，例如，在2004年印度洋海啸救灾过程中，轴辐网络被应用于泰国应急救援系统[96]。......
2025-09-30
-
基于轴辐网络的重大突发事件应急服务问题详细阅读
由于泥石流、暴雨而形成的堰塞体堵塞河道，致使舟曲长达23天浸泡在洪水和污泥当中，千余名官兵、200余台挖掘机连续作战进行应急排险以及河道的清淤工作，才得以使舟曲县城全面退水[86]。在应对重大突发事件的过程中，应急服务需求的特点主要表现如下。......
2025-09-30
-
应急服务设施布局优化理论与应用–解决问题背景详细阅读
应急服务设施为需求点提供服务，即此应急服务设施能够覆盖该需求点。在备用覆盖模型1中，要求每个需求点都必须被服务器覆盖一次的同时，目标是使被覆盖两次的需求点的总价值最大。在实际情况中，可能会因资金预算或政策上的考虑，只能设置固定的P服务器，且某些需求点未能被覆盖到，对此，可使用备用覆盖模型2，该模型是一个双目标优化问题，其目标是将最大化一次覆盖和最大化两次覆盖。应急问题中最显著的特点是强时效性。......
2025-09-30
相关推荐