MQCLP模型在重大突发事件应急设施布局优化中的应用

2023-09-19 理论教育版权反馈

【摘要】：在覆盖问题研究基础上，构建了满足不同服务质量水平下的多重覆盖模型，即多重数量覆盖和多重质量覆盖模型。解决重大突发事件应急服务设施选址问题，首先根据集合覆盖模型，确定在最大临界距离DU内至少需要的应急设施数量PU。设，根据下列模型求解PU：通过上述模型得出满足基本覆盖要求的设施数量PU，对P与PU进行比较，然后确定利用何种模型。如果P＜PU时，采用最大覆盖模型；当P≥PU时，采用多重数量和质量覆盖模型。

在覆盖问题研究基础上，构建了满足不同服务质量水平下的多重覆盖模型（Multi-Quantity&Quality Covering Location Problem，MQCLP），即多重数量覆盖和多重质量覆盖模型。多重数量覆盖是指在满足覆盖距离的情况下，为需求点提供多个设施的覆盖，即多次覆盖；多层级质量覆盖指应急需求点获得不同的、阶梯形的距离覆盖。MQCLP模型具体如下：

在某一灾害应急情景s下，假设

I：应急需求点集合（i∈I）；

J：应急服务设施点候选集合（j∈J）；

P：限定的应急服务设施数量；

pagenumber_ebook=46,pagenumber_book=36 ；

Mi：需求点i的人口数量；

ei：在灾害情景s下，重大地震事故对需求点i的影响程度系数；

βis：在灾害情景s下，重大地震事故对需求点i影响的概率，需求点i在灾害情景s下的需求权重可以用βis×eis×Mi来表示；

Ci：需求点i被覆盖服务水平，0≤Ci≤1，其中，Ci=1表示完全覆盖，Ci=0表示没有设施提供服务；

Qi：根据需求点的重要程度βis×eis×Mi，来确定需求点i至少被覆盖的设施数目；

Dij：需求点i到应急服务设施点j的距离；

psj：在灾害情景s下，应急服务设施j遭破坏，服务能力下降后的能力系数，其中，0≤psj≤1。

建立的多重覆盖模型（MQCLP）如下：

目标函数式（3-7）表示的是在不同服务质量水平下，P个设施所覆盖的人口期望最大；约束条件式（3-8）表示需要布局的设施数目是P；约束条件式（3-9）考虑了灾害对设施服务能力的下降的影响，表示必须保证足够具有服务能力的设施覆盖需求点；约束条件式（3-10）则表示只有当服务设施被选定时，才能为需求点提供服务；约束条件式（3-11）保证xj、zij和ui为二元整数决策变量。

解决重大突发事件应急服务设施选址问题，首先根据集合覆盖模型，确定在最大临界距离DU内至少需要的应急设施数量PU。

设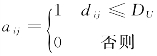 pagenumber_ebook=47,pagenumber_book=37 ，根据下列模型求解PU：

通过上述模型得出满足基本覆盖要求的设施数量PU，对P与PU进行比较，然后确定利用何种模型。如果P＜PU时，采用最大覆盖模型（MCLP）；当P≥PU时，采用多重数量和质量覆盖模型（MQCLP）。

MQCLP模型在重大突发事件应急设施布局优化中的应用

相关推荐