应对大规模应急服务需求的SHSCP模型是在所有网络节点集合中，选择一定数量的节点作为枢纽点，将其余的非枢纽点分配给枢纽点，满足所有约束下，使枢纽数量最少。模型中参数假设如下。例如在应急救援过程中，规定所有的应急救援队伍必须在24小时内到达应急现场并开展救援工作，此时T=24小时。......
2023-09-19
应急服务设施布局优化理论与应用–解决问题背景
【摘要】：应急服务设施为需求点提供服务，即此应急服务设施能够覆盖该需求点。在备用覆盖模型1中，要求每个需求点都必须被服务器覆盖一次的同时，目标是使被覆盖两次的需求点的总价值最大。在实际情况中，可能会因资金预算或政策上的考虑，只能设置固定的P服务器，且某些需求点未能被覆盖到，对此，可使用备用覆盖模型2，该模型是一个双目标优化问题，其目标是将最大化一次覆盖和最大化两次覆盖。应急问题中最显著的特点是强时效性。
应急服务设施为需求点提供服务，即此应急服务设施能够覆盖该需求点。所以，在应急服务设施选址模型中所涉及的基础模型就是覆盖模型，覆盖模型中最经典的两类模型（集合覆盖模型和最大覆盖模型）是其他覆盖问题的基础，而且在此基础上构建的模型一般适用于商业设施选址和应对一般常规突发事件的设施选址问题，其中在上述应急设施选址模型中，存在两个基本假设值得思考。
（1）临界覆盖距离的假设：即如果需求点在临界覆盖距离内，则完全被覆盖，否则，不被覆盖。根据实际情况，此假设过于严格，覆盖距离应有一个机动浮动空间，不同距离的服务设施可提供不同质量水平的服务。
（2）应急服务设施对需求点一次覆盖的假设：这种假设不适用于设施被占用（Busy）或被破坏的情景。重大突发事件会造成多个需求点同时对服务设施的需求，易出现应急服务设施被占用的情况，使得有些需求点无法获得应急服务。Hogan、ReVelle[98]等提出备用覆盖模型（BACOP1&BACOP2）的两次覆盖。
在备用覆盖模型1（BACOP1）中，要求每个需求点都必须被服务器覆盖一次的同时，目标是使被覆盖两次的需求点的总价值最大。在实际情况中，可能会因资金预算或政策上的考虑，只能设置固定的P服务器，且某些需求点未能被覆盖到，对此，可使用备用覆盖模型2（BACOP2），该模型是一个双目标优化问题，其目标是将最大化一次覆盖和最大化两次覆盖。但对不同需求点提供相同质量水平的多次覆盖，将造成资源浪费，同时考虑经济成本等约束，所有需求点的多次完全被覆盖未必可行。所以，根据重大突发事件应急服务的特征，应急设施覆盖选址模型需综合考虑以下三点：
（1）应确定合适的设施选址目标（目标）。
（2）对每个需求点覆盖的设施数目（设施数量）。
（3）设施覆盖需求点的不同距离（服务质量）。
因此，应根据需求点的重要程度（权重）不同，对覆盖质量进行等级划分，采取有所差异的服务质量水平的形式，在满足基本覆盖要求的同时，对重要的需求点进行多重覆盖，同时考虑重大突发事件对服务设施能力破坏等情况，构建数学模型。
应急问题中最显著的特点是强时效性。一般而言，突发事件造成的损失与事件持续时间成正相关关系，应急服务到达时间越早，损失越小，即应急服务设施距离需求点越近，服务越及时，损失则越小。
例如，在我国火灾救援过程中，规定消防队必须在15分钟内到达火灾现场并实施扑救，这样才能有效防止火势蔓延，但火灾有一个最大持续时间，即消防不成功，燃烧物的燃尽自灭时间。火灾损失与扑救延时两者之间的数值关系可近似表示为线性增函数[99]，
即：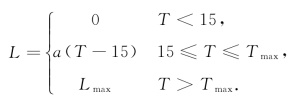
其中 L——火灾损失值；
T——扑救前的火灾延时；
a——损失随扑救延时的增益系数，可考虑各自系统燃烧的对象的价值、易燃性等因素，进行评估得出；
Tmax——火灾最大持续时间，即当消防不成功，可燃物燃尽而自灭的时间；
Lmax——消防不成功时的最大损失值。
根据上述例子，本书对覆盖临界距离的界定引入两个概念，即最小临界距离DL和最大临界距离DU（DL＜DU）。假设需求点在最小临界距离内，则认为完全覆盖，设施提供高质量覆盖服务；需求点在最大临界距离内是基本覆盖，提供一般质量服务；需求点到服务设施的距离超过最大临界距离，则认为不被覆盖。如图3-1所示，设施点1在最小临界范围之内，完全覆盖其服务的需求点i；设施点2在最小临界和最大临界距离中间，为需求点i提供基本覆盖服务；设施点3与需求点i之间的距离超过最大临界距离DU，则不能为需求点i提供服务。以上是关于对覆盖临界距离的界定，也可以用临界时间来代替，即最小临界时间TL和最大临界时间TU（TL＜TU）。
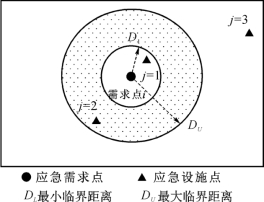
图3-1 不同等级的覆盖水平
不同覆盖距离提供不同覆盖质量水平的阶梯形覆盖模式比较合理，考虑了不同距离的覆盖情况，对于每一个需求点，可能有多个设施对其提供不同覆盖水平的服务。
不同的覆盖距离提供不同的覆盖质量，即覆盖距离和覆盖质量之间存在着一定的函数关系。覆盖满意度函数可表述为覆盖距离（时间）与服务满意率之间的关系来表示。最早提出利用模型中覆盖水平函数替换覆盖或者不被覆盖的两种情况的是Church和Roberts[100]，其他的学者也在此基础上进行了研究，以下是几个可能的覆盖水平函数[101，102]。
设I为应急需求点集合（i∈I）；J为应急服务设施点候选集合（j∈J）；dij为设施点j到需求点i的出行时间；F（dij）表示设施点j到需求点i的响应距离的覆盖服务水平函数；F（dij）可能是连续的或离散的，也可能是线性的或非线性的。
1）线性覆盖满意度函数
线性覆盖满意度函数（Linear Covering Satisfaction Function）是将需求点等待时间或从需求点到服务站的行程距离或行程时间转换成服务满意度的最简便的方法。当需求点数据有限或服务满意水平随等待时间的加长而均匀降低时，可以使用这一函数。函数式（3-1）和图3-2说明了线性覆盖满意度函数的特点。
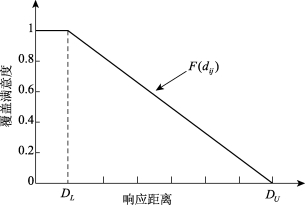
图3-2 线性覆盖满意度函数
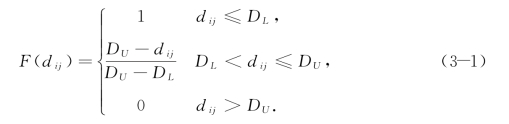
2）凹凸覆盖满意度函数
凹凸覆盖满意度函数（Convex/Concave Covering Satisfaction Function）可以由函数式（3-2）和函数式（3-3）表示，应用于临界阀值DL和DU附近时的时间满意度较敏感的情况，如图3-3所示。
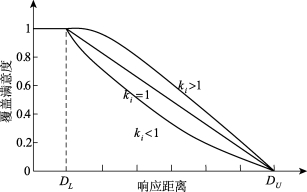
图3-3 凹凸函数覆盖满意度函数
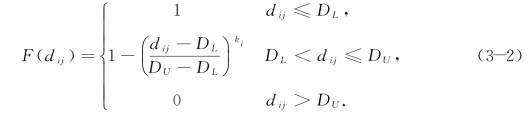
式中ki，∀i∈I是时间敏感系数，当ki＞1时，曲线是凸的；当ki=1时，函数式变成和线性时间满意度曲线相同的函数，在[DL，DU]之间是一条直线；当dij∈[DL，DU]时，函数式（3-2）通过点
呈对称关系的函数可以表述为函数式（3-3）。
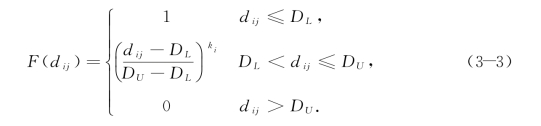
3）余弦分布覆盖满意度函数
余弦分布覆盖满意度函数（Cosine Distributed Covering Satisfaction Function）是从余弦函数曲线的π/2到3π/2的部分截取得到的，该曲线在临界阀值DL和DU附近的覆盖满意度变化较小，曲线中间部分的斜率较大。见函数式（3-4）和图3-4。
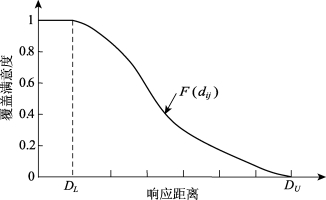
图3-4 余弦分布覆盖满意度函数
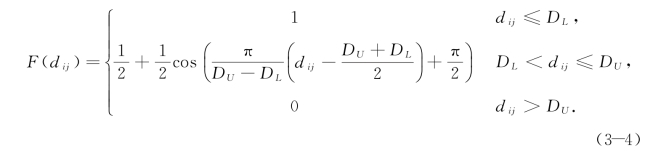
4）离散阶梯形覆盖满意度函数
在阶梯分段函数，用
表示第i个需求点到设施点j之间的距离在
区间时的覆盖满意度，r=1，2，…，R，显然，
，且
，这样，离散阶梯形覆盖函数可以表示成函数式（3-5），图3-5描述了一种可能的离散阶梯形覆盖满意度函数[103]。
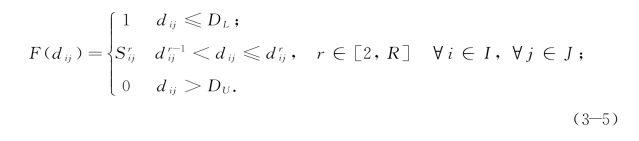
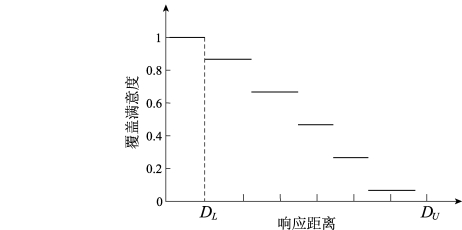
图3-5 一种可能的离散覆盖满意度函数
在本书中，为了模型计算方便，假设覆盖满意度函数随着设施与需求点之间距离的增加而降低，且呈线性关系，当需求点i到设施点j之间的距离dij大于或等于DU时，覆盖满意度函数值为0。
覆盖水平函数与覆盖满意度函数、覆盖的设施数量呈正相关的关系，即覆盖满意度高、覆盖的设施数量多，则覆盖水平高。本书设定覆盖水平函数表达式为
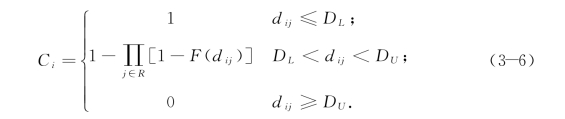
其中，
；R代表覆盖需求点i的服务设施，R⊂J。
有关基于轴辐网络的重大突发事件应急设施布局优化理论与应用的文章
- 详细阅读
-
突发事件应急设施布局优化理论与应用详细阅读
根据突发公共事件的发生过程、性质和机理，突发公共事件主要分为自然灾害、事故灾难、公共卫生事件和社会安全事件四类。根据上述概念的界定，本书中应对重大突发事件的应急服务设施布局是指有效应对各类重大突发事件，提前对永久性的移动类应急服务设施进行规划，确定其数量和位置的过程。......
2023-09-19
-
轴辐网络布局优化：重大突发事件应急设施布局理详细阅读
轴辐网络布局主要集中于两个问题：枢纽点选址问题和非枢纽点分配问题。对于存在单一隶属关系的公共组织或公共机构网络布局属于单分配的轴辐网络，而复杂的快递物流网络大多采用多分配轴辐网络。轴辐网络结构如图1-1所示。轴辐网络主要应用于快递网络、航线优化布局方面。李阳[51]在其博士论文中将轴辐网络理论应用于救灾物流中，构建了轴辐式救灾物流系统框架，并从救灾物资供应、配送和发放三方面对该系统的功能进行了设计。......
2023-09-19
-
重大突发事件应急设施布局优化理论与应用研究详细阅读
根据问题的需要，可以将建设成本、服务效率等问题和容量限制问题综合进行研究。因此，需要进一步研究重大突发事件的历史资料、分析各重大突发事件中应急需求的信息、结合设施点的各种状况，提出并建立符合实际情况的情景集合。在各类数据完备的情况下，将应对本书的应急轴辐网络布局的理论与方法应用到某一类具体应急设施布局中，亦是需要研究与解决的问题。......
2023-09-19
-
应急设施布局优化理论与应用-基于轴辐网络的模详细阅读
Campbell提出的MAHSCP模型有n4+n个变量、2n4+n2个约束式，属于复杂的混合整数规划模型，当节点数超过一定数量时，模型求解面临很大问题。翁克瑞[107]根据MAHSCP模型进行了改进，提出了有n2+n个变量、3n2个约束式的新的多分配枢纽覆盖模型。相对Campbell的MAHSCP模型，MAHSCP2模型减少了输入变量，从而以减少问题的输入规模，节约计算内存和时间。......
2023-09-19
-
基于轴辐网络的重大突发事件应急设施布局优化理详细阅读
折扣系数α依次取值为0.4、0.6和0.8；最大时间约束T分别取值720、960、1 200和1 440分钟；γ*分别取3和5。基于第4章设计的改进的遗传算法，通过算例验证将两模型结果进行比较，并对两个模型的不同参数分析对比。......
2023-09-19
-
基于轴辐网络的应急设施布局优化理论与应用-遗详细阅读
遗传算法对问题的可行解进行编码，通过适应度函数构成优胜劣汰、适者生存的“自然环境”，种群通过遗传、交换、突变等不断演化，产生出新的更加优良的种群，这样经过若干代的进化，最终求得问题的最优解。遗传算法步骤[103]如下：STEP1：选择问题的一个编码；给出一个有N个染色体的初始群体POP，t=1；STEP2：对群体中POP中的每一个染色体popi计算它的适应度函数，fi=fitness[popi]；STEP3：若停止规则满足，则算法停止；否则，计算概率；，2，…......
2023-09-19
-
研究内容：应急服务设施轴辐网络的布局与绕道详细阅读
本书的主要研究内容包括应急服务设施轴辐网络的框架设计、具体选址-分配设计以及鲁棒优化等。4）应急服务设施轴辐网络中的绕道、拥堵优化轴辐网络本身存在着绕道问题，尤其是对于时效性要求比较高的应急服务需求，绕道问题更是成为很大的问题。为此，本书对应急服务设施轴辐网络中的绕道问题进行了研究，设立了“绕道”系数限制。......
2023-09-19
相关推荐