预应力混凝土受弯构件设计计算

1)计算简图

仅在受拉区配置预应力钢筋的预应力混凝土受弯构件，当达到正截面承载力极限状态时，其截面应力状态和钢筋混凝土受弯构件相同。因此，其计算简图也相同。

在受压区也配置预应力钢筋时，由于预拉应力(应变)的影响，受压区预应力钢筋的应力σ′pe与钢筋混凝土受弯构件中的受压钢筋不同，其状态较复杂。随着荷载的不断增大，在预应力钢筋A′p重心处的混凝土压应力和压应变都有所增加，预应力钢筋A′p的拉应力随之减小。故截面到达破坏时，A′p的应力可能仍为拉应力，也可能变为压应力，但其应力值σ′pe却达不到抗压强度设计值f′py，其值可以按平截面假定确定。可按下式计算：

先张法构件：

后张法构件：

预应力混凝土受弯构件正截面受弯破坏时，受拉区预应力钢筋先达到屈服，然后受压区边缘混凝土达到极限压应变而破坏。如果在截面上还有非预应力钢筋As、A′s，破坏时，其应力也都能达到屈服强度。图8.7为矩形截面预应力混凝土受弯构件正截面受弯承载力计算简图。

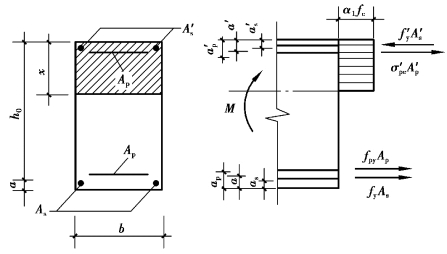
图8.7　矩形截面预应力混凝土受弯构件正截面受弯承载力计算简图

2)正截面受弯承载力计算

对于矩形截面或翼缘位于受拉区的倒T形截面预应力混凝土受弯构件，其正截面受弯承载力计算的基本公式为：

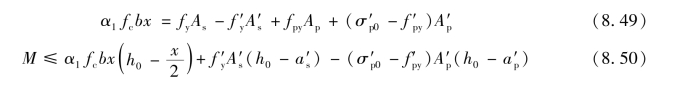
混凝土受压区高度应符合下列条件：

式中　M——弯矩设计值；

As、A′s——受拉区、受压区纵向非预应力钢筋的截面面积；

Ap、A′p——受拉区、受压区纵向预应力钢筋的截面面积；

h0——截面的有效高度；

b——矩形截面的宽度或倒T形截面的腹板宽度；

α1——系数：当混凝土强度等级不超过C50时，α1=1.0，当混凝土强度等级为C80时，α1=0.94，其间按直线内插法确定；

a′——受压区全部纵向钢筋合力点至截面受压边缘的距离，当受压区未配置纵向预应力钢筋或受压区纵向预应力钢筋应力(σ′p0-f′py)为拉应力时，则式(8.52)中的a′用a′s代替；

a′s、a′p——受压区纵向非预应力钢筋合力点、受压区纵向预应力钢筋合力点至截面受压边缘的距离；

σ′p0——受压区纵向预应力钢筋合力点处混凝土法向应力等于零时的预应力钢筋应力。

当x＜2a′时，正截面受弯承载力可按下列公式计算：

式中　as、ap——受拉区纵向非预应力钢筋、受拉区纵向预应力钢筋至受拉边缘的距离。

　　当σ′pe为拉应力时，取x＜2a′s，如图8.8所示。

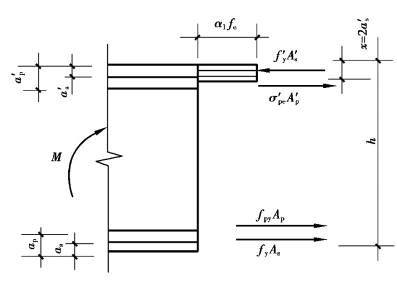
图8.8　矩形截面预应力混凝土受弯构件

(x＜2a′时的正截面受弯承载力计算简图)

3)受弯构件斜截面受剪承载力计算

预应力混凝土梁的斜截面受剪承载力比钢筋混凝土梁大些，主要是由于预应力抑制了斜裂缝的出现和发展，增加了混凝土剪压区高度，从而提高了混凝土剪压区的受剪承载力。

因此，计算预应力混凝土梁的斜截面受剪承载力可在钢筋混凝土梁计算公式的基础上增加一项由预应力而提高的斜截面受剪承载力设计值Vp。根据矩形截面有箍筋预应力混凝土梁的试验结果，Vp的计算公式为：

为此，对矩形、T形及工形截面的预应力混凝土受弯构件，当仅配置箍筋时，其斜截面的受剪承载力按下列公式计算：

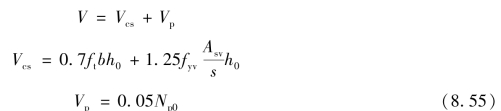
式中　Asv——配置在同一截面内箍筋各肢的全部截面面积：Asv=nAsv1，其中，n为同一截面内箍筋的肢数，Asv1为单肢箍筋的截面面积；

ft——混凝土抗拉强度设计值；

fyv——箍筋抗拉强度设计值；

Np0——计算截面上混凝土法向应力等于零时的预应力钢筋及非预应力钢筋的合力，按式(8.30)、式(8.37)计算；当Np0＞0.3fcA0时，取Np0=0.3fcA0。

对于刻痕钢丝及钢绞线配筋的先张法预应力混凝土构件，如果斜截面受拉区始端在预应力传递长度ltr范围内，则预应力钢筋的合力取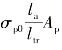，如图8.9所示。la为斜裂缝与预应力钢筋交点至构件端部的距离。

当混凝土法向预应力等于零时，预应力钢筋及非预应力钢筋的合力Np0引起的截面弯矩与由荷载产生的截面弯矩方向相同时，以及对于预应力混凝土连续梁和允许出现裂缝的预应力混凝土简支梁，均取Vp=0。

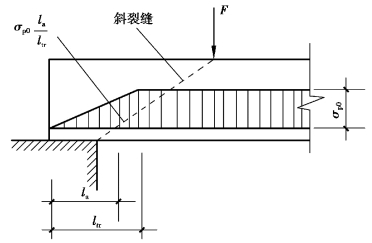
图8.9　预应力钢筋的预应力传递长度范围内有效预应力值的变化

当配有箍筋和预应力弯起钢筋时，其斜截面受剪承载力按下列公式计算：

式中　V——配置弯起钢筋处的剪力设计值，当计算第一排(对支座而言)弯起钢筋时，取用支座边缘处的剪力设计值；当计算以后的每一排弯起钢筋时，取用前一排(对支座而言)弯起钢筋弯起点处的剪力设计值；

Vcs——构件斜截面上混凝土和箍筋的受剪承载力设计值，按式(8.47)计算；

Vp——按式(8.55)计算的由施加预应力所提高的截面的受剪承载力设计值，但在计算Np0时不考虑预应力弯起钢筋的作用；

Asb、Apb——同一弯起平面内非预应力弯起钢筋、预应力弯起钢筋的截面面积；

αs、αp——斜截面上非预应力弯起钢筋、预应力弯起钢筋的切线与构件纵向轴线的夹角。对集中荷载作用下的独立梁(包括作用有多种荷载，且其中集中荷载对支座截面或节点边缘所产生的剪力值占总剪力的75%以上的情况)，其斜截面受剪承载力按下式计算：

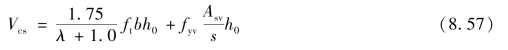
式中　λ——计算截面的剪跨比，可取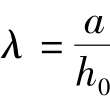，a为计算截面至支座截面或节点边缘距离，计算截面取集中荷载作用点处的截面；当λ＜1.5时，取λ=1.5；当λ＞3时，取λ=3；计算截面至支座之间的箍筋应均匀配置。

为了防止斜压破坏，受剪截面应符合下列条件：

当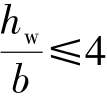时：

当时：

当4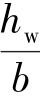＜＜6时，按直线内插法取用。

式中　V——剪力设计值；

b——矩形截面宽度、T形截面或工形截面的腹板宽度；

hw——截面的腹板高度，矩形截面取有效高度h0，T形截面取有效高度扣除翼缘高度，工形截面取腹板净高；

βc——混凝土强度影响系数，当混凝土强度等级不超过C50时，取βc=1.0；当混凝土强度等级为C80时，取βc=0.8；其间按直线内插法取用。

对于矩形、T形、工形截面的一般预应力混凝土受弯构件，当符合下列公式的要求时，则可不进行斜截面受剪承载力计算，仅需按构造要求配置箍筋。

或

前述斜截面受剪承载力计算公式的适用范围和计算位置与钢筋混凝土弯构件的相同。

4)受弯构件使用阶段正截面裂缝控制验算

预应力混凝土受弯构件，在使用阶段按其所处环境类别和结构类别确定相应的裂缝控制等级及最大裂缝宽度限值，并按下列规定进行受拉边缘应力或正截面裂缝宽度验算。

(1)一级——严格要求不出现裂缝的构件

在荷载效应的标准组合下，应符合下列规定：

(2)二级——一般要求不出现裂缝的构件

在荷载效应的标准组合下，应符合下列规定：

在荷载效应的准永久组合下，宜符合下列规定：

式中　σck、σcq——荷载效应的标准组合、准永久组合下抗裂验算边缘混凝土的法向应力：

Mk、Mq——按荷载效应的标准组合、准永久组合计算的弯矩值；

σpc——扣除全部预应力损失后在抗裂验算边缘混凝土的预压应力，按式(8.29)和式(8.35)计算；

W0——换算截面受拉边缘的弹性抵抗矩；

ftk——混凝土抗拉强度标准值。

在施工阶段预拉区出现裂缝的区段，公式(8.62)至式(8.64)中的σpc应乘以系数0.9。

(3)三级——允许出现裂缝的构件

按荷载效应的标准组合并考虑长期作用的影响计算的最大裂缝宽度ωmax按(8.46)式计算，但此时应取αcr=1.7，Ate=0.5bh+(bf-b)hf。按荷载效应的标准组合计算的预应力混凝土构件纵向受拉钢筋的等效应力σsk按下列公式计算：

式中　z——受拉区纵向预应力钢筋和非预应力钢筋合力点至受压区压力合力点的距离，如图8.10所示：

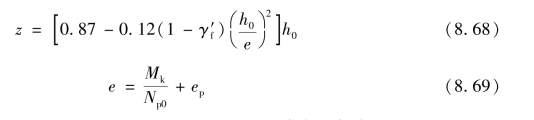
γ′f——受压翼缘截面面积与腹板有效截面面积的比值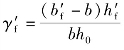，，其中b′f、h′f为受压区翼缘的宽度、高度，当h′f＞0.2h0时，取h′f=0.2h0；

ep——混凝土法向预应等于零时，全部纵向预应力和非预应力钢筋的合力Np0作用点至受拉区纵向预应力和非预应力受拉钢筋合力点的距离。

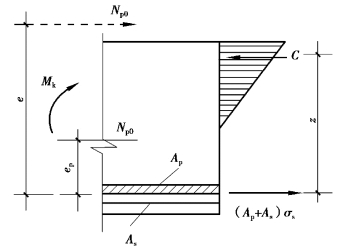
图8.10　预应力钢筋和非预应力钢筋合力点至受压区压力合力点的距离

5)受弯构件斜截面抗裂度验算

《混凝土结构设计规范》(GB 50010—2010)规定，预应力混凝土弯构件斜截面的抗裂度验算，主要是验算截面上的主拉应力σtp和主压应力σcp不超过一定的限值。

(1)斜截面抗裂度验算的规定

①混凝土主拉应力。对严格要求不出现裂缝的构件，应符合下列规定：

对一般要求不出现裂缝的构件，应符合下列规定：

②混凝土主压应力。对严格要求和一般要求不出现裂缝的构件，均应符合下列规定：

式中　σtp、σcp——混凝土的主拉应力和主压应力；

0.85、0.95——考虑张拉时的不准确性和构件质量变异影响的经验系数；

0.6——主要防止腹板在预应力和荷载作用下压坏，并考虑到主压应力过大会导致斜截面抗裂能力降低的经验系数。

　　(2)混凝土主拉应力σtp和主压应力σcp的计算

预应力混凝土构件在斜截面开裂前，基本上处于弹性工作状态，所以主应力可按材料力学方法计算。图8.11所示为一预应力混凝土简支梁，构件中各混凝土微元体除了承受由荷载产生的正应力和剪应力外，还承受由预应力钢筋所引起的预应力。

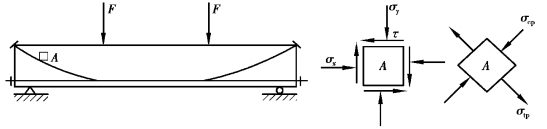
图8.11　配置预应力弯起钢筋Apb的受弯构件中微元件A的应力情况

荷载作用下载面上任一点的正应力和剪应力分别为：

如果梁中仅配置预应力纵向钢筋，则将产生预应力σpcⅡ。在预应力和荷载的联合作用下，计算纤维处产生沿x方向的混凝土法向应力为：

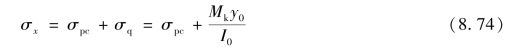
如果梁中还配有预应力弯起钢筋，则不仅产生平行于梁纵轴方向(x方向)的预应力σpcⅡ，而且还要产生垂直于梁纵轴方向(y方向)的预应力σy以及预剪应力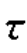pc，其值分别按下式确定：

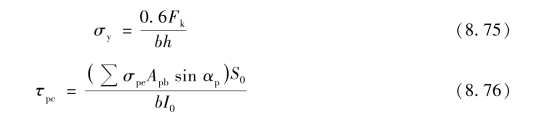
所以，计算纤维处的剪应力为：

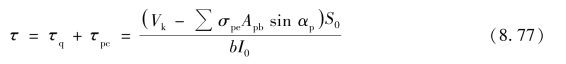
混凝土主拉应力σtp和主压应力σcp按下列公式计算：

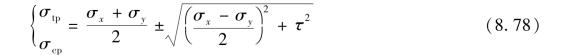
式中　σx——由预应力和弯矩值Mk在计算纤维处产生的混凝土法向应力；

σy——由集中荷载标准值Fk产生的混凝土竖向压应力；

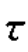——由剪力值Vk和预应力弯起钢筋的预应力在计算纤维处产生的混凝土剪应力；

Fk——集中荷载标准值；

Mk——按荷载标准组合计算的弯矩值；

Vk——按荷载标准组合计算的剪力值；

σpe——预应力弯起钢筋的有效预应力；

S0——计算纤维以上部分的换算截面面积对构件换算截面重心的面积矩；

σpc——扣除全部预应力损失后，在计算纤维处由于预应力产生的混凝土法向应力，按式(8.29)、式(8.35)计算；

y0、I0——换算截面重心到所计算纤维处的距离和换算截面惯性矩；

Apb——计算截面上同一弯起平面内的预应力弯起钢筋的截面面积；

αp——计算截面上预应力弯起钢筋的切线与构件纵向轴线的夹角。

前述公式中σx、σy、σpc和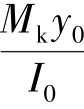，当为拉应力时，以正号代入；当为压应力时，以负号代入。

(3)斜截面抗裂度验算位置

计算混凝土主应力时，应选择跨度范围内不利位置的截面，如弯矩和剪力较大的截面或外形有突变的截面，并且在沿截面高度上，应选择该截面的换算截面重心处和截面宽度有突变处，如工形截面上、下翼缘与腹板交接处等主应力较大的部位。

对先张法预应力混凝土构件端部进行斜截面受剪承载力计算以及正截面、斜截面抗裂验算时，应考虑预应力钢筋在其预应力传递长度ltr范围内实际应力值的变化，如图8.9所示。预应力钢筋的实际预应力按线性规律增大，在构件端部为零，在其传递长度的末端取有效预应力值σpe。

6)受弯构件的挠度与反拱验算

预应力受弯构件的挠度由两部分叠加而成：一部分是由荷载产生的挠度f1l，另一部分是预加应力产生的反拱f2l。

(1)荷载作用下构件的挠度f1l

挠度f1l可按一般材料力学的方法计算，即：

其中截面弯曲刚度B应分别按下列情况计算：

①按荷载效应的标准组合下的短期刚度，可由下列公式计算：

对于使用阶段要求不出现裂缝的构件：

式中　Ec——混凝土的弹性模量；

I0——换算截面惯性矩；

0.85——刚度折减系数，考虑混凝土受拉区开裂前出现的塑性变形。

对于使用阶段允许出现裂缝的构件：

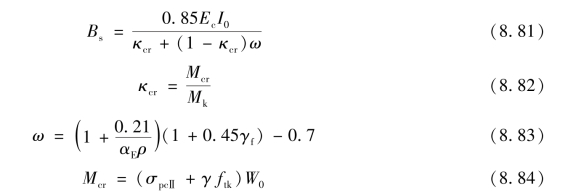
式中　κcr——预应力混凝土受弯构件正截面的开裂弯矩Mcr与荷载标准组合弯矩Mk的比值，当κcr＞1.0时，取κcr=1.0；

γ——混凝土构件的截面抵抗矩塑性影响系数，按附录取用，对矩形截面γm=1.55；

σpcⅡ——扣除全部预应力损失后在抗裂验算边缘的混凝土预压应力；

αE——钢筋弹性模量与混凝土性模量的比值，αE=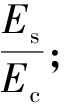

ρ——纵向受拉钢筋配筋率

γf——受拉翼缘面积与腹板有效截面面积的比值，，其中bf、hf为受拉区翼缘的宽度、高度。

对预压时预拉区出现裂缝的构件，Bs应降低10%。

②按荷载效应标准组合并考虑预加应力长期作用影响的刚度，其中Bs按式(8.80)或式(8.81)计算。

(2)预加应力产生的反拱f2l

预应力混凝土构件在偏心距为ep的总预压力Np作用下将产生反拱f2l，其值可按结构力学公式计算，即按两端有弯矩(等于Npep)作用的简支梁计算。设梁的跨度为l，截面弯曲刚度为B，则：

式中的Np、ep及B等按下列不同的情况取用不同的数值，具体规定如下：

①荷载标准组合下的反拱值。荷载标准组合时的反拱值由构件施加预应力引起，按B=0.85EcI0计算，此时的Np及ep均按扣除第一批预应力损失值后的情况计算，先张法构件为Np0Ⅰ、ep0Ⅰ，后张法构件为NpⅠ、epnⅠ。

②考虑预加应力长期影响下的反拱值。预加应力长期影响下的反拱值是由在使用阶段预应力的长期作用引起的，预压区混凝土的徐变变形使梁的反拱值增大，故使用阶段的反拱值可按刚度B=0.425EcI0计算，此时Np及ep应按扣除全部预应力损失后的情况计算，先张法构件为Np0Ⅱ、ep0Ⅱ，后张法构件为NpⅡ、epnⅡ。

(3)挠度计算

由荷载标准组合下构件产生的挠度扣除预应力产生的反拱，即为预应力受弯构件的挠度：

式中　[f]——允许挠度值，参见《混凝土结构设计规范》(GB 50010—2010)表3.3.2。

7)受弯构件施工阶段验算

预应力受弯构件在制作、运输及安装等施工阶段的受力状态，与使用阶段是不相同的。在制作时，截面上受到了偏心压力，截面下边缘受压，上边缘受拉，如图8.12(a)所示。而在运输、安装时，搁置点或吊点通常离梁端有一段距离，两端悬臂部分因自重引起负弯矩，与偏心预压力引起的负弯矩相叠加，如图8.12(b)所示。

在截面上边缘(或称预拉区)，或混凝土的拉应力超过了混凝土的抗拉强度时，预拉区将出现裂缝，并随时间的增长裂缝不断开展。在截面下边缘(预压区)，若混凝土的压应力过大，也会产生纵向裂缝。试验表明，预拉区的裂缝虽可在使用荷载下闭合，对构件的影响不大，但会使构件在使用阶段的正截面抗裂度和刚度降低。因此，必须对构件制作阶段的抗裂度进行验算。《混凝土结构设计规范》(GB 50010—2010)采用限制边缘纤维混凝土应力值的方法，来满足预拉区不允许或允许出现裂缝的要求，同时保证预压区的高压强度。

图8.12　预应力混凝土受弯构件

(1)制作、运输及安装等施工阶段

除进行承载能力极限状态验算外，对不允许出许裂缝的构件或预压时全截面受压的构件，在预加应力、自重及施工荷载作用下(必要时应考虑动力系数)截面边缘的混凝土法向应力应符合下列规定(图8.13)：

式中　σct、σcc——相应施工阶段计算截面边缘纤维的混凝土拉应力和压应力；

f′tk、f′ck——与各施工阶段混凝土立方体抗压强度f′cu相应的抗拉强度标准值、抗压强度标准值，用直线内插法取用。

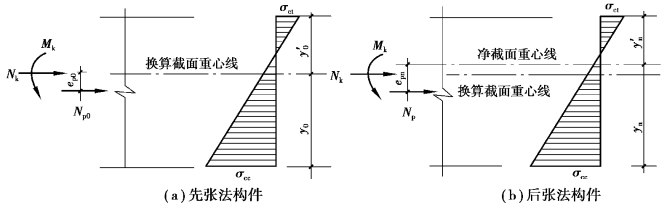
图8.13　预应力混凝土受弯构件施工阶段验算

(2)制作、运输及安装等施工阶段

除进行承载能力极限状态验算外，对预拉区允许出现裂缝的构件，预拉区不配置预应力钢筋时，截面边缘的混凝土法向应力应符合下列条件：

截面边缘的混凝土法向应力σct、σcc可按下式计算：

式中　σpc——由预加应力产生的混凝土法向应力，当σpc为压应力时，取正值；当σpc为拉应力时，取负值；

Nk、Mk——构件自重及施工荷载的标准组合在计算截面产生的轴向力值、弯矩值，当Nk为轴向压力时，取正值；当Nk为轴向拉力时，取负值；对由Mk产生的边缘纤维应力，压应力取正号，拉应力取正号，拉应力取负号；

W0——验算边缘的换算截面弹性抵抗矩。

其余符号都按先张法或后张法构件的截面几何特征代入。