1)计算简图仅在受拉区配置预应力钢筋的预应力混凝土受弯构件，当达到正截面承载力极限状态时，其截面应力状态和钢筋混凝土受弯构件相同。图8.7为矩形截面预应力混凝土受弯构件正截面受弯承载力计算简图。4)受弯构件使用阶段正截面裂缝控制验算预应力混凝土受弯构件，在使用阶段按其所处环境类别和结构类别确定相应的裂缝控制等级及最大裂缝宽度限值，并按下列规定进行......
2023-09-19
预应力混凝土受弯构件应力分析成果
【摘要】：图8.4预应力混凝土受弯构件截面混凝土应力由于对混凝土施加预应力，构件在使用阶段截面不产生拉应力或不开裂。表8.8、表8.9给出了仅在截面受拉区配置预应力钢筋的先张法和后张法预应力混凝土受弯构件在各个受力阶段的应力分析。表8.8先张法预应力混凝土受弯构件各阶段的应力状态续表表8.9后张法预应力混凝土受弯构件各阶段的应力状态图8.5所示为配有预应力钢筋Ap、A′p和非预应力钢筋As、A′s的不对称截面受弯构件。
与预应力轴心受拉构件类似，预应力混凝土受弯构件的受力过程也分两个阶段：施工阶段和使用阶段。每个阶段又包括若干不同的应力过程。
预应力混凝土受弯构件中，预应力钢筋Ap一般都放置在使用阶段的截面受拉区。但是对于梁底受拉区需配置较多预应力钢筋的大型构件，当梁自重在梁顶产生的压力不足以抵消偏心预压力在梁顶受拉区所产生的预拉应力时，往往在梁顶部也需要配置预应力钢筋A′p。对在预压力作用下允许预拉区出现裂缝的中小型构件，可不配置A′p，但需控制其裂缝宽度。为了防止在制作、运输和吊装等施工阶段出现裂缝，在梁的受拉区和受压区通常也配置一些非预应力钢筋As和A′s。
在预应力轴心受拉构件中，预应力钢筋Ap和非预应力钢筋As在截面上是对称布置的，可认为预应力钢筋的总拉力Np作用在截面形心轴上，混凝土受到的预压力是均匀的，即全截面均匀受压。在受弯构件中，如果截面只配置Ap，则预应力钢筋的总拉力Np对截面是偏心的压力，所以混凝土受到的预应是不均匀的，上边缘的预应力和下边缘的预应力分别用σ′pc和σpc表示，如图8.4(a)所示。如果同时配置Ap和A′p(一般Ap＞A′p)，则预应力钢筋Ap和A′p的张拉力的合力Np位于Ap和A′p之间，此时混凝土的预应力图形有两种可能：如果A′p少，应力图形为两个三角形，σ′pc为拉应力；如果A′p较多，应力图形为梯形，σ′pc为压应力，其值小于σpc，如图8.4(b)所示。
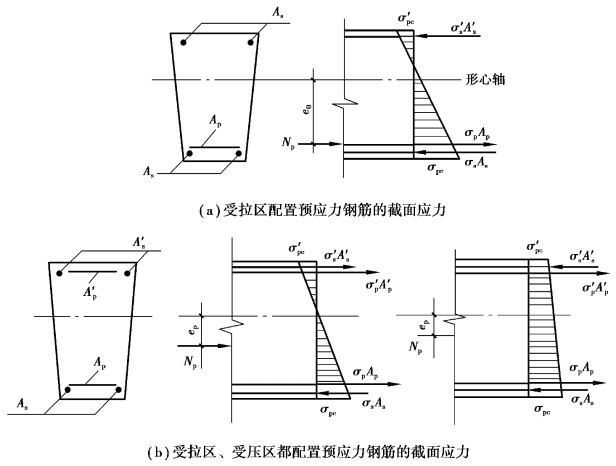
图8.4 预应力混凝土受弯构件截面混凝土应力
由于对混凝土施加预应力，构件在使用阶段截面不产生拉应力或不开裂。因此，不论哪种应力图形，都可以把预应力钢筋的合力视为作用在换算截面上的偏心压力，并把混凝土看作理想弹性体，按材料力学公式计算混凝土的预应力。
表8.8、表8.9给出了仅在截面受拉区配置预应力钢筋的先张法和后张法预应力混凝土受弯构件在各个受力阶段的应力分析。
表8.8 先张法预应力混凝土受弯构件各阶段的应力状态
续表
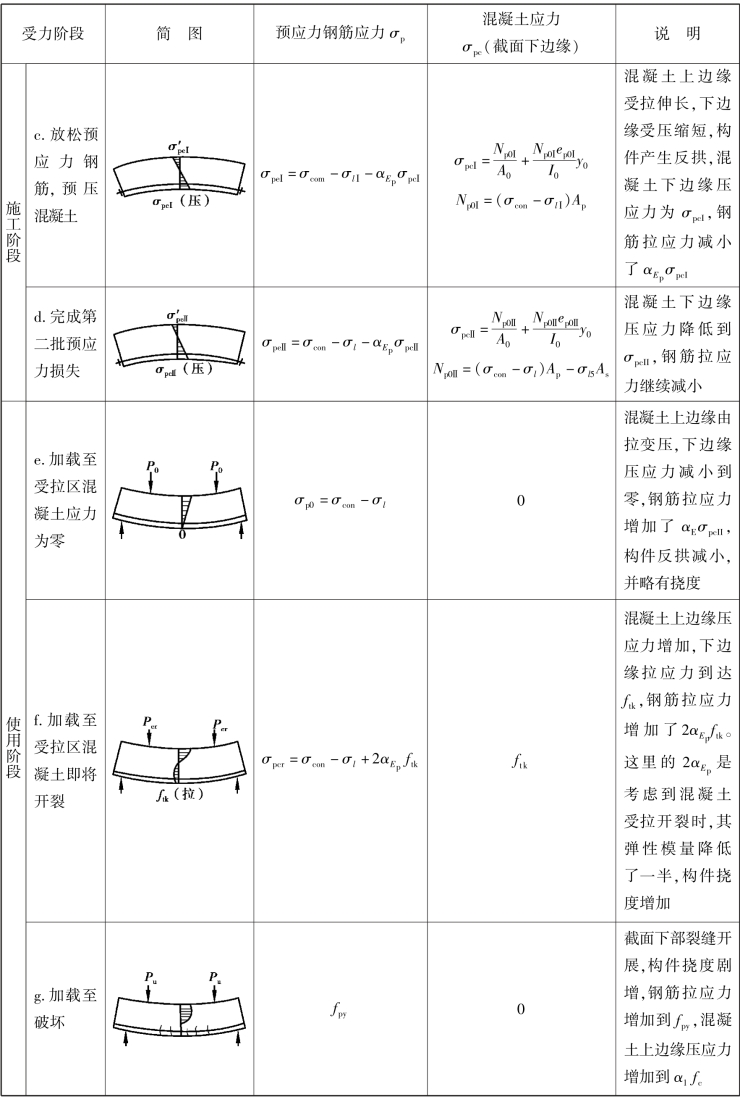
表8.9 后张法预应力混凝土受弯构件各阶段的应力状态
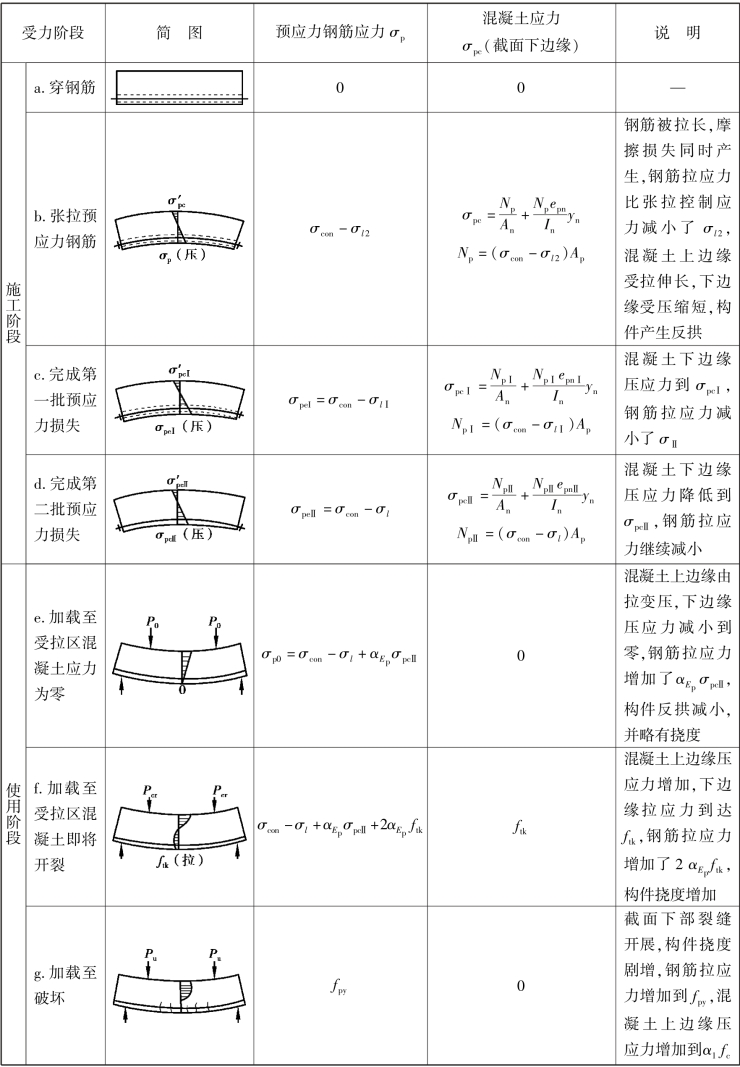
图8.5所示为配有预应力钢筋Ap、A′p和非预应力钢筋As、A′s的不对称截面受弯构件。对照预应力混凝土轴心受拉构件相应各受力阶段的截面应力分析，同理，可得出预应力混凝土受弯构件截面上混凝土法向预应力σpc、预应力钢筋的应力σpe、预应力钢筋和非预应力钢筋的合力Np0(Np)及其偏心距ep0(epn)等的计算公式。
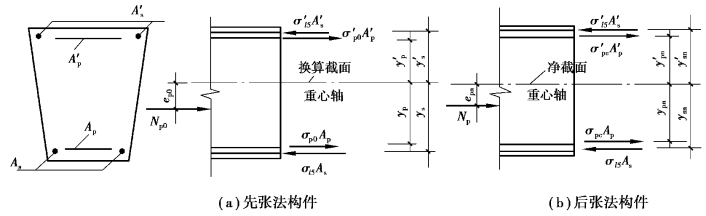
图8.5 配有预应力钢筋和非预应力钢筋的预应力混凝土受弯构件截面
1)施工阶段
(1)先张法构件[图8.5(a)]
按式(8.29)计算求得的σpc值，正号为压应力，负号为拉应力。
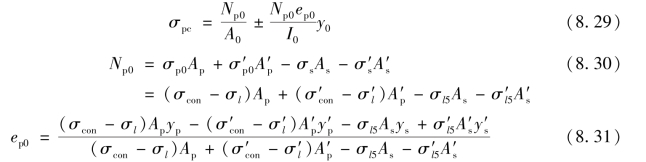
式中 A0——换算截面面积(包括扣除孔道、凹槽等削弱部分以后的混凝土全部截面面积以及全部纵向预应力钢筋和非预应力钢筋截面面积换算成混凝土的截面面积；对由不同混凝土强度等级组成的截面，应根据混凝土弹性模量比值换算成同一混凝土强度等级的截面面积)；
I0——换算截面惯性矩；
y0——换算截面重心至所计算纤维处的距离；
yp、y′p——受拉区、受压区的预应力钢筋合力点至换算截面重心的距离；
ys、y′s——受拉区、受压区的非预应力钢筋重心至换算截面重心的距离；
σp0、σ′p0——受拉区、受压区的预应力钢筋合力点处混凝土法向应力等于零时的预应力钢筋应力。
相应阶段应力钢筋及非预应力钢筋的应力分别为：
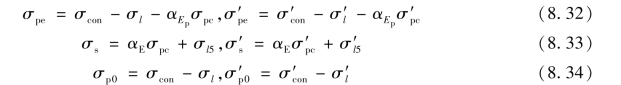
(2)后张法构件[图8.5(b)]
按式(8.35)计算求得的σpc值，正号为压应力，负号为拉应力。
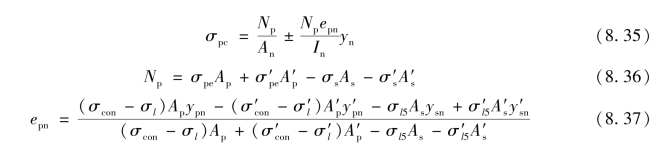
式中 An——混凝土净截面面积(换算截面面积减去全部纵向预应力钢筋截面换算成混凝土的截面面积)，即An=A0-αEpAp或An=Ac+αEAs；
In——净截面惯性矩；
yn——净截面重心至所计算纤维处的距离；
ypn、y′pn——受拉区、受压区预应力钢筋合力点至净截面重心的距离；
ysn、y′sn——受拉区、受压区的非预应力钢筋重心至净截面重心的距离；
σpe、σ′pe——受拉区、受压区预应力钢筋有效预应力。
相应预应力钢筋及非预应力钢筋的应力分别为：
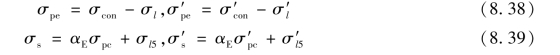
如构件截面中的A′p=0，则式(8.29)—式(8.39)中取σ′l5=0。
需要说明的是，在利用上列公式计算时，均需用施工阶段的有关数值。
2)使用阶段
(1)加载至受拉边缘混凝土应力为零
设在荷载作用下，截面承受弯矩M0[图8.6(c)]，则截面下边缘混凝土的法向拉应力：
欲使这一拉应力抵消混凝土的预压应力σpcⅡ，即σ-σpcⅡ=0，则有：
式中 M0——由外荷载引起的恰好使截面受拉边缘混凝土预压应力为零时的弯矩；
W0——换算截面受拉边缘的弹性抵抗矩。
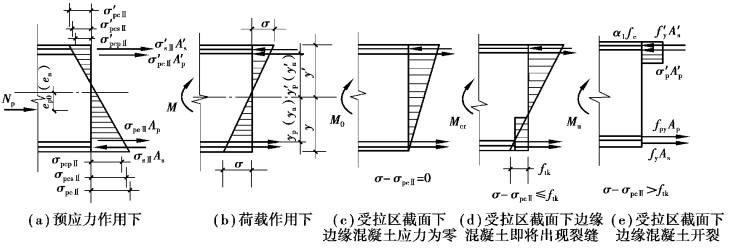
图8.6 受弯构件截面的应力变化
同理，预应力钢筋合力点处混凝土法向应力等于零时，受拉区及受压区的预应力钢筋的应力σp0、σ′p0分别为：
先张法：
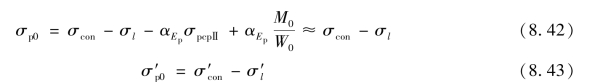
后张法：
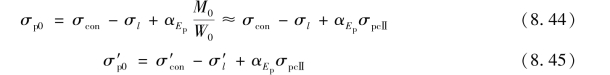
式中 σpcpⅡ——在M0作用下，受拉区预应力钢筋合力处的混凝土法向应力，可近似取等于混凝土截面下边缘的预压应力σpcⅡ。
(2)加载到受拉区裂缝即将出现
混凝土受拉区的拉应力达到混凝土抗拉强度标准值ftk时，截面上受到的弯矩为Mcr，相当于截面在承受弯矩M0=σpcⅡW0后，再增加了钢筋混凝土构件的开裂弯矩
因此，预应力混凝土受弯构件的开裂弯矩为：
即
(3)加载至破坏
当受拉区出现垂直裂缝时，裂缝截面上受拉区混凝土退出工作，拉力全部由钢筋承受。当截面进入第Ⅲ阶段后，受拉钢筋屈服直至破坏。正截面上的应力状态与第4章讲述的钢筋混凝土受弯构件正截面承载力相似，计算方法也基本相同。
有关混凝土结构设计计算的文章
- 详细阅读
-
预应力混凝土受弯构件疲劳验算方法详细阅读
一级裂缝控制等级的预应力混凝土构件的钢筋可不进行疲劳验算。式～式中混凝土压、拉应力以及预应力筋、普通钢筋应力幅计算方法见《混凝土结构设计规范》第6.7.11条。......
2023-08-28
-
预应力受弯构件的钢筋布置及施工方法详解详细阅读
预应力受弯构件可采用T形、工形及箱形等截面。2)预应力纵向钢筋①直线布置：当荷载和跨度不大时，直线布置最为简单，如图8.14所示，施工时用先张法或后张法均可。图8.14预应力钢筋布置②曲线布置、折线布置：当荷载和跨度较大时，可布置成曲线形[图8.14]或折线形[图8.14]。施工时一般用后张法，如预应力混凝土屋面梁、吊车梁等构件。......
2023-09-19
-
混凝土结构轴心受拉构件应力分析详细阅读
预应力混凝土轴心受拉构件从张拉钢筋开始直到构件破坏，截面中混凝土和钢筋应力的变化可以分为两个阶段：施工阶段和使用阶段。先张法轴心受拉构件各阶段的应力状态如表8.5所示。至此，预应力钢筋已完成第一批预应力损失σlI。破坏时，预应力钢筋及非预应力钢筋的拉应力分别达到抗拉强度设计值fpy、fy。......
2023-09-19
-
2.15.8预应力混凝土结构构件详细阅读
无粘结预应力混凝土结构的抗震设计，应符合专门规定。预应力筋穿过框架节点核心区时，节点核心区的截面抗震受剪承载力应按第2.15.6节的有关规定进行验算，并可考虑有效预加力的有利影响。板柱节点应符合2.15.9的规定。......
2023-08-28
-
混凝土结构受弯构件截面弯曲刚度计算详细阅读
在荷载长期作用下，构件截面弯曲刚度将会降低，致使构件的挠度增大。此外，受拉区和受压区混凝土的收缩不一致，使梁发生翘曲，也将导致曲率增大和刚度降低。2)截面弯曲刚度前面讲了弯矩的标准组合值Mk，现在简单介绍弯矩的准永久组合值Mq。而书库等建筑物的楼面活荷载中，准永久荷载值占的比例将达到80%。受弯构件挠度验算时，采用的截面弯曲刚度B是在它的短期刚度Bs的基础上，用弯矩的准永久组合值Mq计算得来的。......
2023-09-19
- 详细阅读
-
混凝土受弯构件的挠度限值与裂缝控制等级简明指详细阅读
受弯构件的挠度限值与裂缝控制等级见表1-19。表1-19 受弯构件的挠度限值与裂缝控制等级表1-20 受弯构件的挠度限值注：1.表中l0为构件的计算跨度；计算悬臂构件的挠度限值时，其计算跨度l0按实际悬臂长度的2倍取用。表1-21 结构构件的裂缝控制等级及最大裂缝宽度的限值 注：1.对处于年平均相对湿度小于60%地区一类环境下的受弯构件，其最大裂缝宽度限值可采用括号内的数值。......
2023-08-31
相关推荐