在荷载长期作用下，构件截面弯曲刚度将会降低，致使构件的挠度增大。此外，受拉区和受压区混凝土的收缩不一致，使梁发生翘曲，也将导致曲率增大和刚度降低。2)截面弯曲刚度前面讲了弯矩的标准组合值Mk，现在简单介绍弯矩的准永久组合值Mq。而书库等建筑物的楼面活荷载中，准永久荷载值占的比例将达到80%。受弯构件挠度验算时，采用的截面弯曲刚度B是在它的短期刚度Bs的基础上，用弯矩的准永久组合值Mq计算得来的。......
2023-09-19
混凝土结构设计计算：短期截面弯曲刚度分析结果
【摘要】：前面讲过，截面弯曲刚度就是使截面产生单位曲率需要施加的弯矩值。把式、式和式、式代入Bs的基本表达式中，即得短期截面弯曲刚度Bs的计算公式：式中，当h′f＞0.2 h0时，取h′f=0.2 h0计算。式适用于矩形、T形、倒T形和工形截面受弯构件，由该式计算的平均曲率与试验结果符合较好。③当其他条件相同时，截面有效高度h0对截面弯曲刚度的影响最显著。
截面弯曲刚度不仅随弯矩(或者说荷载)的增大而减小，而且还将随荷载作用时间的增长而减小。这里先讲不考虑时间因素的短期截面弯曲刚度，记作Bs。
1)Bs的基本表达式
研究变形、裂缝的钢筋混凝土试验梁如图7.8所示。
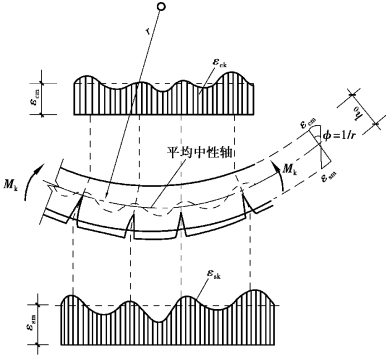
图7.8 纯弯段内的平均应变
纯弯区段内，弯矩Mk=0.5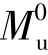 
～0.7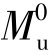 
时，测得的钢筋和混凝土的应变情况如下：
①沿梁长，各正截面上受拉钢筋的拉应变和受压区边缘混凝土的压应变都是不均匀分布的，裂缝截面处最大，分别为εsk、εck，裂缝与裂缝之间逐渐变小，呈曲线变化。这里εsk、εck的第2个下标“k”表示它们是由弯矩的标准组合值Mk产生的。
②沿梁长，截面受压区高度是变化的，裂缝截面处最小，因此沿梁长中性轴呈波浪形变化。
③当量测范围比较长(≥750 mm)时，则各水平纤维的平均应变沿截面高度的变化符合平截面假定。
根据平截面假定，可得纯弯区段的平均曲率：
式中 r——与平均中性轴相对应的平均曲率半径；
εsm，εcm——纵向受拉钢筋重心处的平均拉应变和受压区边缘混凝土的平均压应变，这里第二个下标“m”表示平均值；
h0——截面的有效高度。
前面讲过，截面弯曲刚度就是使截面产生单位曲率需要施加的弯矩值。因此，短期截面弯曲刚度为：
式(7.32)中，Mk称为弯矩的标准组合值：挠度验算时要用荷载标准直，由荷载标准值在截面上产生的弯矩称为弯矩的标准值，为了区别于弯矩设计值M，故添加下标“k”；荷载有多种，如结构自重的永久荷载、楼面活荷载等，把每一种荷载标准值在同一截面上产生的弯矩标准值组合起来就是弯矩的标准组合值。
2)平均应变εsm和εcm
纵向受拉钢筋的平均应变εsm可以由裂缝截面处纵向受拉钢筋的应变εsk来表达，即：
式中，φ为裂缝间纵向受拉钢筋应变不均匀系数。
图7.9所示为第Ⅱ阶段裂缝截面的应力图。对受压区合压力点取矩，可得裂縫截面处纵向受拉钢筋的应力：
式中 η——正常使用阶段裂縫截面处的内力臂系数。
图7.9 第Ⅱ阶段裂缝截面的应力图
研究表明，对常用的混凝土强度等级及配筋率，可近似地取：
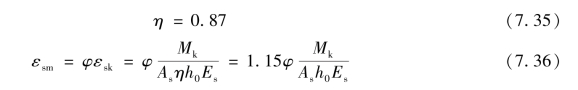
另外，通过试验研究，对受压区边缘混凝土等级及配筋率，可近似地取：
以上公式中，Es、Ec分别为钢筋、混凝土的弹性模量，ξ为受压区边缘混凝土平均应变综合系数。
3)裂缝间纵向受拉钢筋应变不均匀系数φ
图7.10所示沿一根试验梁的梁长，实测的纵向受拉钢筋的应变分布图。由图7.10可见，在纯弯区段A—A内，钢筋应变是不均匀的，裂缝截面处最大应变为εsk，离开裂缝截面就逐渐减小，这是由于裂缝间的受拉混凝土参加工作，承担部分拉力的缘故。图7.10中的水平虚线表示平均应变εsm=φεsk。因此，系数φ反映了受拉钢筋应变的不均匀性，其物理意义就是裂缝间受拉混凝土参加工作，减小了变形和裂缝宽度。φ越小，说明裂缝间受拉混凝土帮助纵向受拉钢筋承担的拉力越大，εsm降低得越多，对增大截面弯曲刚度、减小变形和裂缝宽度的贡献越大。φ越大，则效果相反。
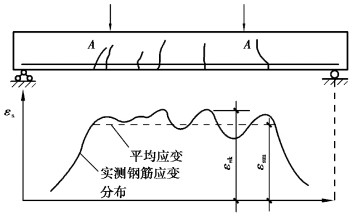
图7.10 纯弯曲段内受拉钢筋的应变分布
试验表明，随着荷载(或弯矩)的增大，εsm与εsk间的差距逐渐减小，也就是说，随着荷载(或弯矩)的增大，裂缝间受拉混凝土逐渐退出工作。当εsm=εsk时，即φ=1，此时裂缝间受拉混凝土全部退出工作。当然，φ不可能大于1。φ的大小还与有效受拉混凝土截面面积计算、考虑钢筋黏结性能差异后的有效纵向受拉钢筋配筋率ρte有关。这是因为参加工作的受拉混凝土主要是指钢筋周围的那部分有效范围内的受拉混凝土面积。当ρte较小时，说明参加受拉的混凝土相对面积大些，对纵向受拉钢筋应变的影响程度也相应大些，因此φ就小一些。
对轴心受拉构件，有效受拉混凝土截面面积Ate即为构件的截面面积。对受弯(即偏心受压和偏心受拉)构件，按图7.11采取计算，并近似取：
此外，φ值还受到截面尺寸的影响，即φ随截面高度的增加而增大。
试验研究表明，φ可近似表达为：
式中 σsq——与计算最大裂缝宽度时的相同，即按荷载准永久组合计算的钢筋混凝土构件纵向受拉普通钢筋应力。
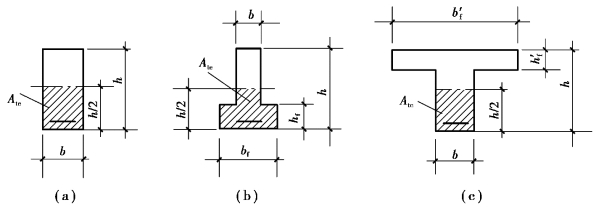
图7.11 有效受拉混凝土面积
对于受弯构件：
式中 Mq——按荷载准永久组合计算的截面弯矩。
当φ＜0.2时，取φ=0.2；当φ＞1时，取φ=1；对直接承受重复荷载的构件，取φ=1。
按有效受拉混凝土截面面积计算的纵向受拉钢筋配筋率ρte为：
在最大裂缝宽度和挠度验算中，当ρte＜0.01时，都取ρte=0.01。
4)Bs的计算公式
国内外试验资料表明，受压区边缘混凝土平均应变综合系数ξ与αEρ及受压翼缘加强系数γ′f有关。为简化计算，可直接给出αEρ/ξ的值：
式中，αE=Es/Ec，γ′f=(b′f-b)h′f/(bh0)，即γ′f等于受压翼缘截面面积与腹板有效截面面积的比值。
把式(7.33)、式(7.36)和式(7.37)、式(7.42)代入Bs的基本表达式(7.32)中，即得短期截面弯曲刚度Bs的计算公式：
式中，当h′f＞0.2 h0时，取h′f=0.2 h0计算。γ′f因为当翼缘较厚时，靠近中性轴的翼缘部分受力较小，如仍按全部h′f计算γ′f，将使Bs的计算值偏高。在荷载效应的标准组合作用下，受压钢筋对刚度的影响不大，计算时可不考虑。如需估计其影响，可在γ′f计算式中加入αEρ′，即：
式中 ρ′——受压钢筋的配筋率，ρ′=A′s/(bh0)。
式(7.43)适用于矩形、T形、倒T形和工形截面受弯构件，由该式计算的平均曲率与试验结果符合较好。
综上可知，短期截面弯曲刚度Bs是受弯构件纯弯区段在承受50%～70%的正截面受弯承载力Mu的第Ⅱ阶段区段内，考虑了裂缝间受拉混凝土的工作，即纵向受拉钢筋应变不均匀系数φ，也考虑了受压区边缘混凝土压应变的不均匀性，从而用纯弯区段的平均曲率来求得Bs的。对Bs可有以下认识：
①Bs主要用纵向受拉钢筋来表达，其计算公式表面复杂，实际上比用混凝土表达更简单。
②Bs不是常数，随弯矩而变化，弯矩Mk增大，Bs减小；Mk减小，Bs增大，这种影响通过φ来反映。
③当其他条件相同时，截面有效高度h0对截面弯曲刚度的影响最显著。
④当截面有受拉翼缘或有受压翼缘时，都会使Bs有所增大。
⑤具体计算表明，纵向受拉钢筋配筋率ρ增大，Bs也略有增大。
⑥在常用配筋率ρ=1%～2%的情况下，提高混凝土强度等级对提高Bs的作用不大。
⑦Bs的单位与弹性材料的EI一样，都是“N/mm2”，因为弯矩的单位是“N·mm”，截面曲率的单位是“1/mm”。
有关混凝土结构设计计算的文章
- 详细阅读
-
截面弯曲刚度的定义及计算详细阅读
对于承受弯矩的截面来说，抵抗截面转动的能力，就是截面弯曲刚度。由式知，截面弯曲刚度EI越大，挠度f越小。为了便于工程应用，截面弯曲刚度的确定采用以下两种简化方法。此外，还要求所给出的截面弯曲刚度必须适合于用手算的方法来进行挠度验算。可以理解到，这样定义的截面弯曲刚度就是弯矩由零增加到0.5 Mu～0.7 Mu过程中，截面弯曲刚度的总平均值。......
2023-09-19
-
混凝土结构设计计算实例及计算表分析与结果详细阅读
图4.18按照抗剪要求计算各截面所需弯起钢筋的数量对于跨中截面：故不需设置剪力钢筋的区段长度。表4.4各排弯起钢筋起弯点设计弯矩计算表根据表4.4所示各截面设计弯矩值Mdx绘制设计弯矩图。图4.19按抗弯承载力要求计算各排弯起钢筋起弯......
2023-09-19
-
混凝土结构设计计算：斜截面破坏形态详细阅读
根据大量的试验观测，钢筋混凝土梁的斜截面剪切破坏，大致可归纳为3种主要破坏形态。图4.3斜截面剪切破坏形态剪压破坏[图4.3]当剪跨比适中，且梁内配置的腹筋数量适当时，常发生剪压破坏。除了前述3种主要破坏形态外，在不同的条件下，斜截面还可能出现其他破坏形态，如局部挤压破坏、纵向钢筋的锚固破坏等。因此，《公路桥规》给出的斜截面抗剪承载力计算公式，都是依据这种破坏形态的受力特征为基础建立的。......
2023-09-19
-
混凝土结构斜截面弯曲破坏位置详细阅读
按照式和式进行斜截面抗弯承载力计算时，首先应确定最不利斜截面位置。式中Vd——斜截面受压端正截面处相应于最大弯矩的剪力组合设计值。公式按荷载产生的破坏力矩与构件极限抗弯力矩之差为最小的原则导出，其物理意义是满足此式要求的斜截面其抗弯承载力最小。设计配置纵向钢筋时，正截面抗弯承载力已得到保证。可以证明满足上述构造要求，部分钢筋弯起使与斜截面相交的纵向钢筋减少。......
2023-09-19
-
混凝土结构设计计算：受弯构件正截面破坏特征详细阅读
梁内纵向受力钢筋数量用配筋率ρ表示，配筋率是纵向受力钢筋截面面积As与截面有效面积的百分比。构件的破坏特征取决于配筋率、混凝土的强度等级、截面形式等诸多因素，其中配筋率的影响最大。配筋率不同，受弯构件破坏形式不同。当构件的配筋率超过一定值时，构件的破坏是由于混凝土被压碎而引起的。图3.10受弯构件正截面破坏形态综上所述，受弯构件的破坏是受拉钢筋和受压混凝土相互抗衡的结果。......
2023-09-19
-
排架内力计算的结果-混凝土结构设计详细阅读
任意荷载作用下等高排架的内力计算，需要首先求解单阶超静定柱在各种荷载作用下的柱顶反力。图3-42 任意荷载作用下的等高排架内力分析2.不等高排架的内力计算不等高排架在任意荷载作用下，由于高、低跨的柱顶移位不相等，因此，不能用剪力分配法求解，通常用力法进行分析。下面以图3-43a所示两跨不等高排架为例，说明其内力计算方法。解力法方程求得未知力x1、x2后，就可通过平衡条件求得该两跨不等高排架各柱的内力。......
2023-08-30
-
混凝土结构设计计算-矩形截面偏心受压构件承载详细阅读
1)区分大、小偏心受压破坏形态的界限第3章中讲的正截面承载力计算的基本假定同样也适用于偏心受压构件正截面受压承载力的计算。图5.18大偏心受压截面承载力计算简图①计算公式。矩形截面小偏心受压构件正截面受压承载力的基本计算公式小偏心受压破坏时，受压区边缘混凝土先被压碎，受压钢筋A′s的应力达到屈服强度，而远侧钢筋As可能受拉或受压，可能屈服也可能不屈服。......
2023-09-19
相关推荐