对称配筋的矩形截面钢筋混凝土双向偏心受拉构件，其正截面受拉承载力应符合下列规定：式中 Nu0——构件的轴心受拉承载力设计值；e0——轴向拉力作用点至截面重心的距离；Mu——按轴向拉力作用下的弯矩平面计算的正截面受弯承载力设计值。该梁跨中截面按矩形截面偏心受拉构件计算所需的下部纵向受力钢筋面积As，与下列何项数值最为接近？2900 35005900 7100答案：解答：1.判别大小偏心情况图2.5-5 梁截面及跨中配筋图属小偏心受拉构件。......
2023-08-28
混凝土结构偏心受拉构件正截面受拉承载力计算
【摘要】：1)大偏心受拉构件正截面承载力计算当轴向拉力作用在As合力点及A′s合力点以外时，截面虽开裂，但还有受压区，否则拉力N得不到平衡。图6.3大偏心受拉构件截面受拉承载力计算简图对称配筋时，由于As=A′s和fy=f′y，将其代入基本公式(6.2)后，必然会求得x为负值，即属于x＜2 a′s的情况。图6.4小偏心受拉构件截面受拉承载力计算简图在这种情况下，不考虑混凝土的受拉工作。
1)大偏心受拉构件正截面承载力计算
当轴向拉力作用在As合力点及A′s合力点以外时，截面虽开裂，但还有受压区，否则拉力N得不到平衡。既然还有受压区，截面不会裂通，这种情况称为大偏心受拉。
图6.3所示为矩形截面大偏心受拉构件的计算简图。构件破坏时，钢筋As及A′s的应力都达到屈服强度，受压区混凝土强度达到α1 fc。
基本公式如下：
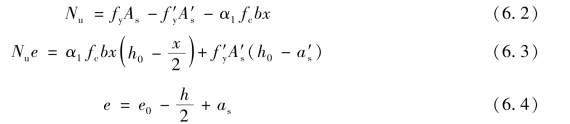
受压区的高度应当符合x≤xb的条件，计算中考虑受压钢筋时，还要符合x≥2 a′s的条件。
设计时，为了使钢筋总用量(As+A′s)最少，与偏心受压构件一样，应取x=xb，代入式(6.3)及式(6.2)，可得：
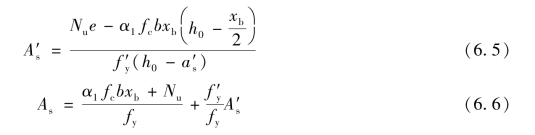
式中 xb——界限破坏时受压区高度，xb=ξbh0。
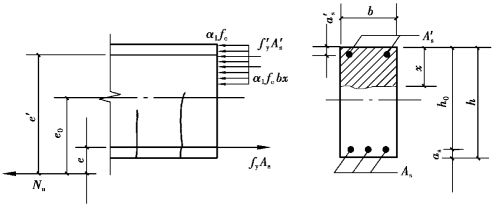
图6.3 大偏心受拉构件截面受拉承载力计算简图
对称配筋时，由于As=A′s和fy=f′y，将其代入基本公式(6.2)后，必然会求得x为负值，即属于x＜2 a′s的情况。此时，可按偏心受压的相应情况类似处理，即取x=2 a′s，并对A′s合力点取矩和取A′s=0分别计算As值，最后按所得较小值配筋。
其他情况的设计题和复核题的计算与大偏心受压构件相似，所不同的是轴向力为拉力。
2)小偏心受拉构件正截面承载力计算
在小偏心拉力作用下，临近破坏前，一般情况是截面裂缝全部贯通。拉力完全由钢筋承担，其计算简图如图6.4所示。
图6.4 小偏心受拉构件截面受拉承载力计算简图
在这种情况下，不考虑混凝土的受拉工作。设计时，可假定构件破坏时钢筋As及A′s的应力都达到屈服强度。根据内外力分别对钢筋As及A′s的合力点取矩的平衡条件，可得：
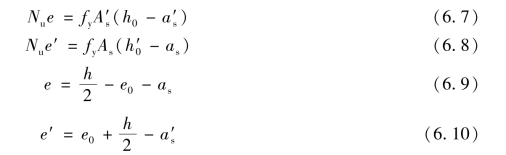
对称配筋时，可取：
《混凝土结构设计规范》(GB 50010—2010)规定：轴心受拉及小偏心受拉杆件的纵向受力钢筋不得采用绑扎接头。
【例6.2】 如图6.5所示，已知某矩形水池，壁厚为300 mm。通过内力分析，求得跨中水平方向每米宽度上最大弯矩设计值M=120 kN·m，相应的每米宽度上的轴向拉力设计值N=240 kN。该水池的混凝土强度等级为C25，钢筋用HRB400级。求水池在该处需要的As及A′s值。
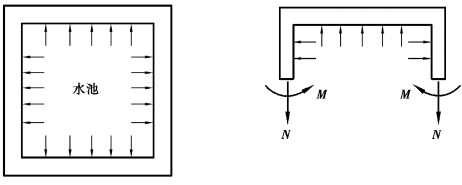
图6.5 矩形水池池壁弯矩M和拉力N示意图
【解】 令N=Nu，M=Nue0，b×h=1000 mm×300 mm；取as=a′s=35 mm。
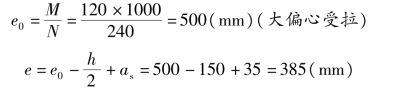
先假定x=xb=0.518h0=0.518×265≈137(mm)来计算A′s值，因为这样能使(As+A′s)的用量最少。
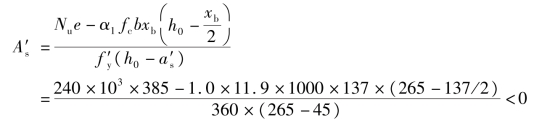
取A′s=ρ′minbh=0.002×1000×300=600 mm2，选用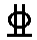
12@180 mm(A′s=628 mm2)。
该题由计算A′s及As的问题转化为已知A′s求As的问题。此时，x不再是界限值xb，必须重新求算x值，计算方法和偏心受压构件计算相同。由式(6.3)计算x值。将式(6.3)转化成下式：
代入数据得：
化简得：
求解得：
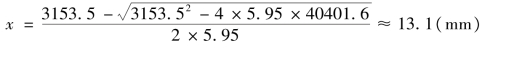
x=13.1 mm＜2a′s=90 mm，取x=2a′s，并对A′s合力点取距，可求得：
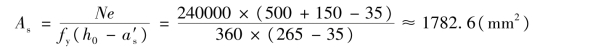
另外，当不考虑A′s，即取A′s=0，由式(6.3)重求x值。
代入数据得：
化简得：
求解得：
由式(6.2)重求得As值：
从上面计算中取小者配筋(即在As=1782.6 mm2和1696 mm2中取小的值配筋)。
取As =1696 mm2来配筋，选用直径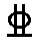
14@90 mm(As =1710 mm2)。
有关混凝土结构设计计算的文章
- 详细阅读
-
混凝土结构设计计算：偏心受拉构件的力学特征详细阅读
大偏心受拉构件的受力特点是：当拉力增大到一定程度时，受拉钢筋首先达到抗拉屈服强度；随着受拉钢筋塑性变形的增长，受压区面积逐步缩小；最后构件由于受压区混凝土达到极限应变而破坏。其破坏形态与小偏心受压构件相似。小偏心受拉构件的受力特点是：混凝土开裂后，裂缝贯穿整个截面，全部轴向拉力由纵向钢筋承担；当纵向钢筋达到屈服强度时，截面即达到极限状态。......
2023-09-19
-
2.5.3大偏心受拉构件正截面承载力计算|结详细阅读
当纵向拉力作用在As合力点以外时，属于大偏心受拉构件。图2.5-3所示为矩形截面大偏心受拉构件的受力情况。图2.5-3 大偏心受拉构件承载力计算图在设计时为了使钢筋总用量最少，与偏心受压构件一样，应取受压区高度x=ξbh0，代入式及式可得若按式求得的As′＜ρminbh，则可先按构造要求或最小配筋率配置As′，变为已知As′求As的情况。......
2023-08-28
-
混凝土结构轴心受拉构件应力分析详细阅读
预应力混凝土轴心受拉构件从张拉钢筋开始直到构件破坏，截面中混凝土和钢筋应力的变化可以分为两个阶段：施工阶段和使用阶段。先张法轴心受拉构件各阶段的应力状态如表8.5所示。至此，预应力钢筋已完成第一批预应力损失σlI。破坏时，预应力钢筋及非预应力钢筋的拉应力分别达到抗拉强度设计值fpy、fy。......
2023-09-19
-
混凝土T形截面梁受弯构件正截面承载力计算详细阅读
它与原矩形截面相比较，承载能力相同，但节省了混凝土，减轻了自重。T形截面梁受力后，翼缘受压时的压应力沿翼缘宽度方向的分布不均匀，离梁肋越远，压应力越小。因此，受压翼缘的计算宽度应有一定限制，在此宽度范围内的应力分布可假设是均匀的，且能与梁肋很好地整体工作。图3.18T形截面的应力分布图表3.6T形及倒L形截面受弯构件翼缘计算宽度b′f注：①表中b为梁的腹板宽度。......
2023-09-19
-
混凝土结构设计计算：受弯构件正截面破坏特征详细阅读
梁内纵向受力钢筋数量用配筋率ρ表示，配筋率是纵向受力钢筋截面面积As与截面有效面积的百分比。构件的破坏特征取决于配筋率、混凝土的强度等级、截面形式等诸多因素，其中配筋率的影响最大。配筋率不同，受弯构件破坏形式不同。当构件的配筋率超过一定值时，构件的破坏是由于混凝土被压碎而引起的。图3.10受弯构件正截面破坏形态综上所述，受弯构件的破坏是受拉钢筋和受压混凝土相互抗衡的结果。......
2023-09-19
-
混凝土结构受弯构件截面弯曲刚度计算详细阅读
在荷载长期作用下，构件截面弯曲刚度将会降低，致使构件的挠度增大。此外，受拉区和受压区混凝土的收缩不一致，使梁发生翘曲，也将导致曲率增大和刚度降低。2)截面弯曲刚度前面讲了弯矩的标准组合值Mk，现在简单介绍弯矩的准永久组合值Mq。而书库等建筑物的楼面活荷载中，准永久荷载值占的比例将达到80%。受弯构件挠度验算时，采用的截面弯曲刚度B是在它的短期刚度Bs的基础上，用弯矩的准永久组合值Mq计算得来的。......
2023-09-19
-
正截面受弯承载力计算方法详细阅读
表2.3-2 T形、I形及倒L形截面受弯构件翼缘计算宽度bf′注：1.表中b为腹板宽度。此类T形的受弯承载力计算基本公式仍可由力的平衡和力矩平衡得出。求正截面承载力Mu。故属于第一类T形。解答：1.判断T形截面类型故为第二类T形。......
2023-08-28
相关推荐