1)截面设计对称配筋时,截面两侧的配筋相同,即As=A′s,fy=f′y。代入式即可求得钢筋面积:2)截面复核可按不对称配筋的截面复核方法进行验算,但取As=A′s,fy=f′y。已知条件同例5.4,设计成对称配筋。本题与例5.4比较可以看出,当采用对称配筋时,钢筋用量需要多一些。综上可知,在矩形截面偏心受压构件的正截面受压承载力计算中,能利用的只有力与力矩两个平衡方程式。......
2023-09-19
与构件正截面受弯承载力计算一样,偏心受压构件正截面受压承载力的计算也分为截面设计与截面复核两类问题。计算时,首先要确定是否要考虑P-δ效应。
1)截面设计
这时构件截面上的内力设计值N、M、材料及构件截面尺寸为已知,欲求As和A′s。计算步骤为:先算出偏心距ei,初步判别截面的破坏形态,当ei>0.3 h0时,可先按大偏心受压情况计算;当ei≤0.3h0时,则先按属于小偏心受压情况计算,然后应用有关计算公式求得钢筋截面面积As及A′s。求出As、A′s后再计算x,用x≤xb、x>xb来检查原先假定的是否正确,如果不正确需要重新计算。在所有情况下,As及A′s还要满足最小配筋率的规定,同时(As+A′s)不宜大于bh的5%。最后,要按轴心受压构件验算垂直于弯矩作用平面的受压承载力。
(1)大偏心受压构件的截面设计
分为A′s未知与A′s已知的两种情况。
①已知:截面尺寸b×h,混凝土的强度等级,钢筋种类(一般情况下As及A′s取同一种钢筋),轴向力设计值N及弯矩设计值M,长细比lc/h,求钢筋截面面积As及A′s。
令N=Nu,M=Ne0,从式(5.10)和式(5.11)中可看出,共有x、As和A′s 3个未知数,而只有两个方程式,所以与双筋受弯构件类似。为了使钢筋(As+A′s)的总用量为最小,应取x=xb=ξbh0,代入式(5.11),得钢筋A′s的计算公式:
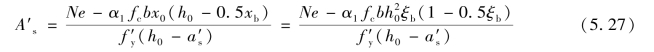
将求得的A′s及x=ξbh0代入式(5.10),则得:

最后,按轴心受压构件验算垂直于弯矩作用平面的受压承载力。当其不小于N值时,满足要求;否则要重新设计。
②已知:b,h,N,M,fc,fy,f′y,lc/h及受压钢筋A′s的数量,求钢筋截面面积As。
令N=Nu,M=Ne0,从式(5.10)及式(5.11)可看出,仅有x及As两个未知数,完全可以通过式(5.10)和式(5.11)的联立,直接求算As的值,但要解算x的二次方程,相当麻烦。对此可仿照第3章中双筋截面已知A′s时的情况,令Mu2=α1 fc bx(h0-x/2),由式(5.11)知Mu2=Nef′yA′s(h0-α′s),再算出αs=Mu2/α1 fcb ,于是ξ=1-(h0-x/2),代入式(5.10)求出As。尚需注意,若求得x>ξbh0,就应改用小偏心受压重新计算;如果仍用大偏心受压计算,则要采取大截面尺寸或提高混凝土强度等级、加大A′s的数量等措施,也可按A′s未知的情况来重新计算,使其满足x<ξbh0的条件。若x<2 a′s,仿照双筋受弯构件的办法,对受压钢筋A′s合力点取矩,计算As值,得:
,于是ξ=1-(h0-x/2),代入式(5.10)求出As。尚需注意,若求得x>ξbh0,就应改用小偏心受压重新计算;如果仍用大偏心受压计算,则要采取大截面尺寸或提高混凝土强度等级、加大A′s的数量等措施,也可按A′s未知的情况来重新计算,使其满足x<ξbh0的条件。若x<2 a′s,仿照双筋受弯构件的办法,对受压钢筋A′s合力点取矩,计算As值,得:

另外,再按不考虑受压钢筋A′s,即取A′s=0,利用式(5.10)、式(5.11)求算As值,然后与用式(5.29)求得的A′s值作比较,取其中较小值配筋。最后,按轴心受压构件验算垂直于弯矩作用平面的受压承载力。
由前述可知,大偏心受压构件的截面设计方法,不论A′s是未知还是已知,都基本上与双筋受弯构件相仿。
(2)小偏心受压构件正截面承载力设计
这时未知数有x、As和A′s 3个,而独立的平衡方程式只有两个,故必须补充一个条件才能求解。注意,式(5.20)并不能作为补充条件,因为式中的ξ=x/h0,建议按以下两个步骤进行截面设计。
①确定As,作为补充条件。当ξcy<ξ且ξ>ξb时,不论As配置多少,它总是不屈服的。为了经济,可取As=ρmin,同时考虑到防止反向破坏的要求,As按以下方法确定:当N≤fcbh时,取As=0.002bh;当N>fcbh时,As由反向受压破坏的式(5.26)求得,如果As<0.002bh,取As=0.002bh。
②求出ξ值,再按ξ的3种情况求出A′s。把As代入力的平衡方程式(5.17)和力矩平衡方程式(5.18)中,消去A′s,得:

求ξ值后,按上述小偏心受压的3种情况分别求出A′s。
a.ξcy>ξ>ξb时,把ξ代入力的平衡方程式或力矩平衡方程式中,即可求出A′s。
b.h/h0>ξ≥ξcy时,取σs=-f′y按下式重新求ξ:
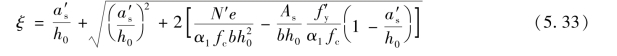
再按式(5.17)求出A′s。
c.ξ≥ξcy且ξ≥ 时,取x=h,σs=-f′y,由式(5.17)得:
时,取x=h,σs=-f′y,由式(5.17)得:

如果以上求得的As值小于0.002bh,应取A′s=0.002bh。
2)承载力复核
进行承载力复核时,一般已知b、h、As和A′s,混凝土强度等级及钢筋级别,构件长细比lc/h0。分为两种情况:一种是已知轴向力设计值,求偏心距e0,即验算截面能承受的弯矩设计值M;另一种是已知e0,求轴向力设计值。不论哪一种情况,都需要进行垂直于弯矩作用平面的承载力复核。
(1)弯矩作用平面的承载力复核
①已知轴向力设计值N,求弯矩设计值M。先将已知配筋和ξb代入式(5.10)计算界限情况下的受压承载力设计值Nub。如果N≤Nuh,则为大偏心受压,可按式(5.10)求x,再将x代入式(5.11)求e,则得弯矩设计值M=Ne0;如果N>Nuh,则为小偏心受压,应按式(5.17)和式(5.20)求x,再将x代入式(5.18)求e,由式(5.13)、式(15.14)求得e0及M=Ne0。
另一种方法是,先假定ξ≤ξb,由式(5.10)求出x,如果ξ=x/h0≤ξb,说明假定是对的,再由式(5.11)求e0;如果ξ=x/h0>ξb,说明假定有误,则应按式(5.17)、式(5.20)求出x,再由式(5.18)求出e0。
②已知偏心距e0,求轴向力设计值N。因截面配筋已知,故可按图5.18对N作用点取矩求x。当x≤xb时,则为大偏压,将x及已知数据代入式(5.10)可求解出轴向力设计值N即为所求;当x>xb时,则为小偏心受压,将已知数据代入式(5.17)、式(5.18)和式(5.20)联立求解轴向力设计值N。
综上可知,在进行弯矩作用平面的承载力复核时,与受弯构件正截面承载力复核一样,总是要求出x才能使问题得到解决。
(2)垂直于弯矩作用平面的承载力复核
无论是设计题或截面复核题,是大偏心受压还是小偏心受压,除了在弯矩作用平面内依照偏心受压进行计算外,都要验算垂直于弯矩作用平面的轴心受压承载力。此时,应考虑φ值,并取b作为截面高度。
【例5.4】 已知:荷载作用下柱的轴向力设计值N=396 kN,杆端弯矩设计值M1=0.92M2,M2=218 kN·m,截面尺寸:b=300 mm,h=400 mm,as=a′s=40 mm;混凝土强度等级为C30,钢筋采用HRB400级;lc/h=6。求钢筋截面面积A′s及As。
【解】 因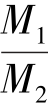 =0.92>0.9,故需要考虑P-δ效应。
=0.92>0.9,故需要考虑P-δ效应。
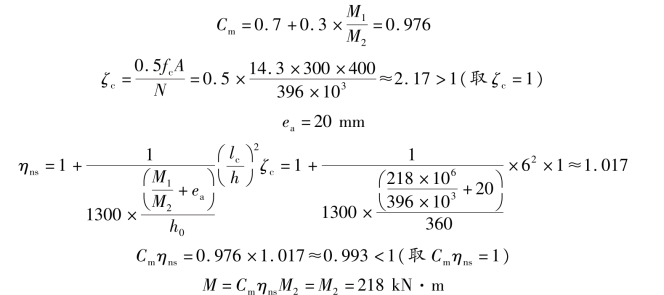
则

因ei=571 mm>0.3h0=0.3×360=108(mm)(先按大偏压情况计算)

由式(5.27)得:

由式(5.28)得:
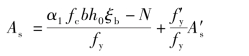
![]()
受拉钢筋As选用3 22+2
22+2 20(As=1768 mm2),受压钢筋A′s选用2
20(As=1768 mm2),受压钢筋A′s选用2 18+1
18+1 14(A′s=662.9 mm2)。
14(A′s=662.9 mm2)。
由式(5.10),求出x:
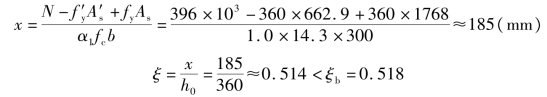
故前面假定为大偏心受压是正确的。
垂直于弯矩作用平面的承载力经验算满足要求,此处略。
【例5.5】 已知柱的轴向压力设计值N=4600 kN,杆端弯矩设计值M1=0.5 M2,M2=130 kN·m,截面尺寸为b=400 mm,h=600 mm,as=a′s=45 mm,混凝土强度等级为C35,fc=16.7 N/mm2,采用HRB400级钢筋,lc=l0=3 m。求钢筋截面面积As和A′s。
【解】 轴压比![]() ,故要考虑P-δ效应。
,故要考虑P-δ效应。
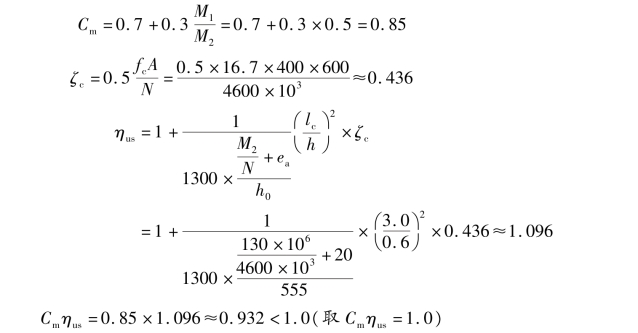
故弯矩设计值:
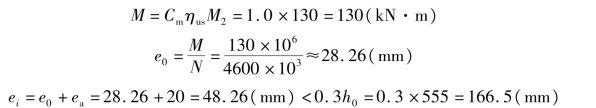
故初步按小偏心受压计算,并分为两个步骤。
①确定As。由N=4600 kN>fbh=16.7×400×600=4008 kN,故令N=Nu,按反向破坏公式(5.28)或公式(5.29)求As。
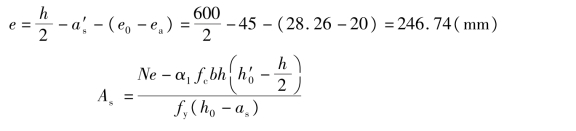
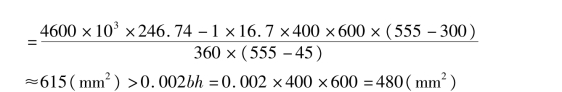
因此,取As=615 mm2作为补充条件。
②求ξ并按ξ的情况求A′s。
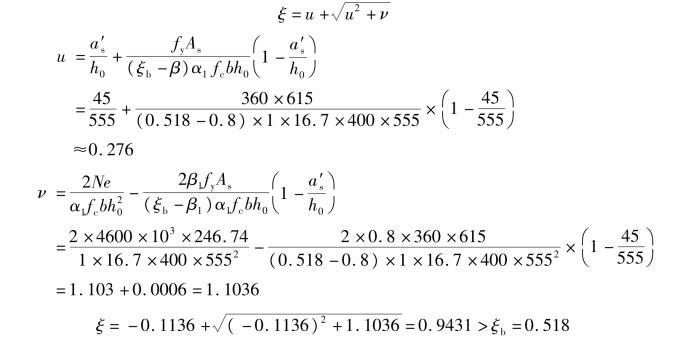
故确定是小偏心受压。
ξcy=2β-ξb=2×0.8-0.518=1.082>ξ=0.9431
故属于小偏心受压的第一种情况:ξcy>ξ>ξb,由力的平衡方程得:

对As采用3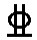 16,As=603(mm2);对A′s采用4
16,As=603(mm2);对A′s采用4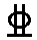 25,A′s=1966(mm2)。
25,A′s=1966(mm2)。
再验算垂直弯矩作用平面的轴心受压承载力。由![]() ,查表5.1,得φ=1.0。按式(5.4)得:
,查表5.1,得φ=1.0。按式(5.4)得:

以上是理论计算的结果,As与A′s相差太大。为了实用,可加大As,使A′s减小,但(A′s+As)的用量将增加。
有关混凝土结构设计计算的文章

1)截面设计对称配筋时,截面两侧的配筋相同,即As=A′s,fy=f′y。代入式即可求得钢筋面积:2)截面复核可按不对称配筋的截面复核方法进行验算,但取As=A′s,fy=f′y。已知条件同例5.4,设计成对称配筋。本题与例5.4比较可以看出,当采用对称配筋时,钢筋用量需要多一些。综上可知,在矩形截面偏心受压构件的正截面受压承载力计算中,能利用的只有力与力矩两个平衡方程式。......
2023-09-19

单筋矩形截面正截面受弯承载力计算简图如图2.3-5所示。图2.3-5 单筋矩形截面正截面受弯承载力计算简图经济配筋率的范围为:板 ρ=0.4%~0.8%矩形梁 ρ=0.6%~1.5%T形梁 ρ=0.9%~1.8%。 一矩形截面简支梁承受弯矩设计值M=230kN·m,采用C20级混凝土,fc=9.6MPa,HRB400级钢筋,fy=360MPa。......
2023-08-28

在实际工作中,斜截面抗剪承载力计算可分为斜截面抗剪承载能力复核和抗剪配筋设计两种情况。《公路桥规》规定,受弯构件斜截面抗剪承载力的验算位置,应按下列规定采用。2)抗剪配筋设计进行抗剪配筋设计时,荷载产生的剪力组合设计值应由混凝土、箍筋和弯起钢筋共同承担。②计算以后各排弯起钢筋时,取用计算前排弯起钢筋时的剪力设计值截面加一倍有效梁高处,应由弯起钢筋承担的那部分剪力设计值。......
2023-09-19

1)区分大、小偏心受压破坏形态的界限第3章中讲的正截面承载力计算的基本假定同样也适用于偏心受压构件正截面受压承载力的计算。图5.18大偏心受压截面承载力计算简图①计算公式。矩形截面小偏心受压构件正截面受压承载力的基本计算公式小偏心受压破坏时,受压区边缘混凝土先被压碎,受压钢筋A′s的应力达到屈服强度,而远侧钢筋As可能受拉或受压,可能屈服也可能不屈服。......
2023-09-19

钢筋混凝土结构是由配置受力的普通钢筋或钢筋骨架的混凝土制成的结构。在这种情况下,钢筋的作用主要是协助混凝土共同承受拉力。钢筋混凝土结构的刚度较大,在使用荷载作用下的变形较小,故可有效地用于对变形有要求的建筑物中。随着钢筋混凝土结构的不断发展,上述缺点已经或正在逐步加以改善。......
2023-09-19

同一截面在不同荷载组合下出现正、负号弯矩。图2.3-8 双筋截面计算简图2.基本公式及适用条件双筋矩形截面受弯承载力的计算公式可以根据图2.3-8所示的计算简图由力和力矩的平衡条件得出:式中 αs=ξ基本公式的适用条件是:1.ξ≤ξb该条件是避免超筋的条件,保证受拉区钢筋先屈服,然后混凝土被压碎。......
2023-08-28

根据大量的试验观测,钢筋混凝土梁的斜截面剪切破坏,大致可归纳为3种主要破坏形态。图4.3斜截面剪切破坏形态剪压破坏[图4.3]当剪跨比适中,且梁内配置的腹筋数量适当时,常发生剪压破坏。除了前述3种主要破坏形态外,在不同的条件下,斜截面还可能出现其他破坏形态,如局部挤压破坏、纵向钢筋的锚固破坏等。因此,《公路桥规》给出的斜截面抗剪承载力计算公式,都是依据这种破坏形态的受力特征为基础建立的。......
2023-09-19

梁内纵向受力钢筋数量用配筋率ρ表示,配筋率是纵向受力钢筋截面面积As与截面有效面积的百分比。构件的破坏特征取决于配筋率、混凝土的强度等级、截面形式等诸多因素,其中配筋率的影响最大。配筋率不同,受弯构件破坏形式不同。当构件的配筋率超过一定值时,构件的破坏是由于混凝土被压碎而引起的。图3.10受弯构件正截面破坏形态综上所述,受弯构件的破坏是受拉钢筋和受压混凝土相互抗衡的结果。......
2023-09-19
相关推荐