图2.4-18所示为双向偏心受压构件，纵向钢筋一般沿截面四周布置。双向偏心受压构件的正截面在双向偏心压力N作用下，中和轴是倾斜的，与y轴有一个φ的夹角。对于沿周边布置钢筋的单向偏心受压构件的承载力计算仍需根据平截面假定计算钢筋的应力。......
2023-08-28
混凝土结构设计计算-矩形截面偏心受压构件承载力计算
【摘要】：1)区分大、小偏心受压破坏形态的界限第3章中讲的正截面承载力计算的基本假定同样也适用于偏心受压构件正截面受压承载力的计算。图5.18大偏心受压截面承载力计算简图①计算公式。矩形截面小偏心受压构件正截面受压承载力的基本计算公式小偏心受压破坏时，受压区边缘混凝土先被压碎，受压钢筋A′s的应力达到屈服强度，而远侧钢筋As可能受拉或受压，可能屈服也可能不屈服。
1)区分大、小偏心受压破坏形态的界限
第3章中讲的正截面承载力计算的基本假定同样也适用于偏心受压构件正截面受压承载力的计算。与受弯构件相似，利用平截面假定，规定了受压区边缘极限压应变值的数值后，就可以求得偏心受压构件正截面在各种破坏情况下，沿截面高度的平均应变分布(图5.17)。
在图5.17中，εcu表示受压区边缘混凝土极限压应变值；εy表示受拉纵筋屈服时的应变值；ε′y表示受压纵筋屈服时的应变值，ε′y=f′y/Es；xcb表示界限状态时按应变的截面中性轴高度。
从图5.17可以看出，当受压区达到xcb时，受拉纵筋达到屈服。因此，相应于界限破坏形态的相对受压区高度ξb根据第3章确定。
当ξ≤ξb时，属大偏心受压破坏形态；ξ＞ξb时，属小偏心受压破坏形态。
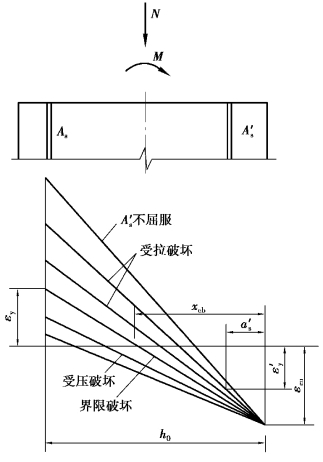
图5.17 偏心受压构件正截面在各种破坏情况时沿截面高度的平均应变分布
2)矩形截面偏心受压构件正截面的承载力计算
(1)矩形截面大偏心受压构件正截面受压承载力的基本计算公式
按受弯构件的处理方法，把受压区混凝土曲线压应力图用等效矩形图形来替代，其应力值取α1fc，受压区高度取为x，故大偏心受压破坏的截面计算简图如图5.18所示。
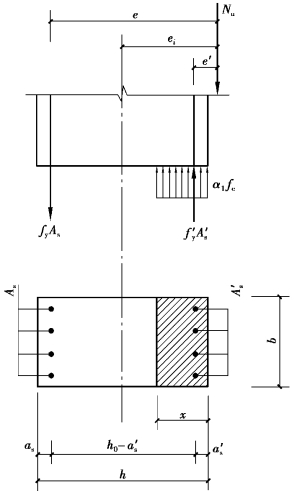
图5.18 大偏心受压截面承载力计算简图
①计算公式。由力的平衡条件及各力对受拉钢筋合力点取矩的力矩平衡条件，可以得到下面两个基本计算公式：
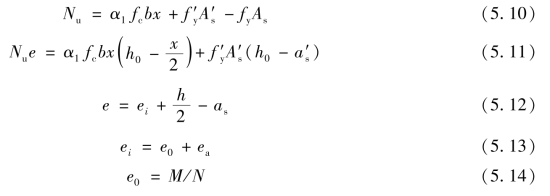
式中 Nu——受压承载力设计值；
α1——系数，混凝土强度调整系数取1.0；
e——轴向力作用点至受拉钢筋As合力点之间的距离，见式(5.12)；
ei——初始偏心距，见式(5.13)；
e0——轴向力对截面重心的偏心距；
ea——附加偏心距，其值取偏心方向截面尺寸的1/30和20 mm中的较大者；
M——控制截面弯矩设计值，考虑P-δ二阶效应；
N——与M相应的轴向压力设计值；
x——混凝土受压区高度。
②适用条件。为了保证构件破坏时受拉区钢筋应力先达到屈服强度fy，要求满足：
式中 xb——界限破坏时的混凝土受压区高度，xb=ξbh0，ξb与受弯构件的相同。
为了保证构件破坏时，受压钢筋应力能达到屈服强度f′y，与双筋受弯构件一样，要求满足：
式中 a′s——纵向受压钢筋合力点至受压区边缘的距离。
(2)矩形截面小偏心受压构件正截面受压承载力的基本计算公式
小偏心受压破坏时，受压区边缘混凝土先被压碎，受压钢筋A′s的应力达到屈服强度，而远侧钢筋As可能受拉或受压，可能屈服也可能不屈服。
小偏心受压可分为3种情况：
①ξcy＞ξ＞ξb，这时As受拉或受压，但都不屈服，如图5.19(a)所示；
②h/h0＞ξ≥ξcr，这时As受压屈服，但x＜h，如图5.19(b)所示；
③ξ＞ξcr，且ξ≥h/h0，这时As受压屈服，且全截面受压，如图5.19(c)所示。
ξcr为As受压屈服时的相对受压区高度。
假定As是受拉的，如图5.19(a)所示，根据力的平衡条件及力矩平衡条件得：
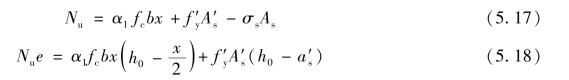
或
式中 x——混凝土受压区高度，当x＞h时，取x=h；
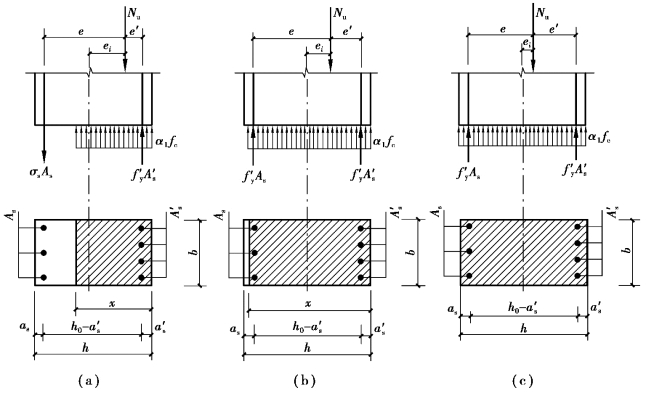
图5.19 小偏心受压截面承载力计算简图
σs——钢筋As的应力值，可根据截面应变保持平面的假定计算，亦可近似取：
要求满足-f′y≤σs≤fy；
xb——界限破坏时的混凝土受压区高度，xb=ξbh0；
ξ、ξb——分别为相对受压区高度和相对界限受压区高度；
e、e′——分别为轴向力作用点至受拉钢筋As合力点和受压钢筋A′s合力点之间的距离：
在x≤h0(即ξ＜1)的情况下，可利用图5.19(a)的应变关系图推导出下列公式：
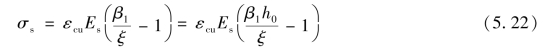
式中，系数β1是混凝土受压区高度x与截面中性轴高度xc的比值系数(即x=β1xc)。当混凝土强度等级不超过C50时，β1=0.8(详见第3章)。但用式(5.23a)计算钢筋应力σs时，需要利用式(5.18)和式(5.19)求解x值，势必要解x的三次方程，不便于手算。
根据我国试验资料分析，实测的钢筋应变εs与ξ接近直线关系，其线性回归方程为：
由于σs对小偏压截面承载力影响较小，考虑界限条件ξ=ξb时，Es=fy/Es；ξ=β1时，εs=0，调整回归方程(5.23a)后，简化成下式：
在式(5.20)中，令σs=-f′y，则可得到As受压屈服时的相对受压区高度：
(3)矩形截面小偏心受压构件及向破坏的正截面承载力计算
当偏心距很小，A′比As大得多，且轴向力很大时，截面的实际形心轴偏向A′s，导致偏心方向的改变，有可能在离轴向力较远一侧的边缘混凝土先压坏的情况，称为反向受压破坏。这时的截面承载力计算简图如图5.20所示。
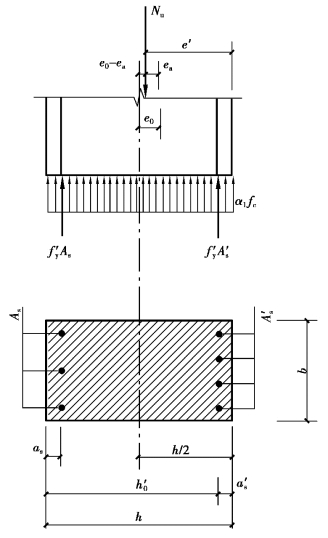
图5.20 反向破坏时的截面承载力计算简图
这时，附加偏心距ea反向了，使e0减小，即：
对A′s合力点取矩，得：
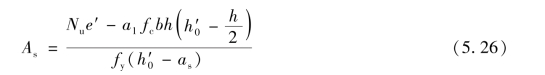
截面设计时，令Nu=N，按式(5.26)求得的As应不小于ρmin(ρmin=0.2%)，否则应取As=0.002bh。
数值分析表明，只有当N＞a1 fcbh时，按式(5.26)求得的As才有可能大于0.002bh；当N≤a1 fcbh时，求得的As总是小于0.002bh。所以《混凝土结构规范》(GB 50010—2010)规定，当N＞fcbh时，尚应验算反向受压破坏的承载力。
有关混凝土结构设计计算的文章
- 详细阅读
-
混凝土结构偏心受拉构件正截面受拉承载力计算详细阅读
1)大偏心受拉构件正截面承载力计算当轴向拉力作用在As合力点及A′s合力点以外时，截面虽开裂，但还有受压区，否则拉力N得不到平衡。图6.3大偏心受拉构件截面受拉承载力计算简图对称配筋时，由于As=A′s和fy=f′y，将其代入基本公式(6.2)后，必然会求得x为负值，即属于x＜2 a′s的情况。图6.4小偏心受拉构件截面受拉承载力计算简图在这种情况下，不考虑混凝土的受拉工作。......
2023-09-19
-
混凝土结构设计计算：轴心受压螺旋箍筋柱正截面详细阅读
根据前述分析可知，螺旋箍筋或焊接环筋所包围的核心截面混凝土因处于三向受压状态，故其轴心抗压强度高于单轴向的轴心抗压强度。如在正截面受压承载力计算中考虑间接钢筋的作用时，箍筋间距不应大于80 mm及dcor/5，也不小于40 mm。......
2023-09-19
-
偏心受压构件正截面受压破坏形态的设计计算详细阅读
试验表明，钢筋混凝土偏心受压短柱的破坏形态有受拉破坏和受压破坏两种。图5.14偏心受压构件截面实测的平均应变分布2)偏心受压长柱的破坏类型试验表明，钢筋混凝土柱在承受偏心受压荷载后，会产生纵向弯曲。其中，曲线ABCD表示某钢筋混凝土偏心受压构件截面材料破坏时的承载力M与N之间的关系。这表明构件长细比的加大会降低构件的正截面受压承载力。......
2023-09-19
-
2.4.2轴心受压构件正截面承载力计算-结果详细阅读
正截面受压承载力计算 根据以上分析，如图2.4-4所示，在考虑长柱承载力的降低和可靠度的调整因素后，轴心受压构件承载力计算公式为N≤Nu=0.9φ 式中 N——轴向压力设计值；A——构件截面面积；As′——全部纵向受压钢筋截面面积；fc——混凝土的轴心抗压强度设计值；fy′——纵向钢筋的抗压强度设计值；φ——钢筋混凝土构件的稳定系数，按表2.4-1采用。......
2023-08-28
-
混凝土结构计算：轴心受压箍筋柱正截面承载力详细阅读
图5.3配有纵向钢筋的柱最常见的轴心受压柱是普通箍筋柱。1)受力分析和破坏形态配有纵向钢筋和箍筋的短柱，在轴心荷载作用下，整个截面的应变基本上是均匀分布的。2)承载力计算公式根据前述分析，配有纵向钢筋和普通箍筋的轴心受压短柱破坏时，横截面的计算应力图形如图5.8所示。......
2023-09-19
-
混凝土T形截面梁受弯构件正截面承载力计算详细阅读
它与原矩形截面相比较，承载能力相同，但节省了混凝土，减轻了自重。T形截面梁受力后，翼缘受压时的压应力沿翼缘宽度方向的分布不均匀，离梁肋越远，压应力越小。因此，受压翼缘的计算宽度应有一定限制，在此宽度范围内的应力分布可假设是均匀的，且能与梁肋很好地整体工作。图3.18T形截面的应力分布图表3.6T形及倒L形截面受弯构件翼缘计算宽度b′f注：①表中b为梁的腹板宽度。......
2023-09-19
-
混凝土结构设计计算：受弯构件正截面破坏特征详细阅读
梁内纵向受力钢筋数量用配筋率ρ表示，配筋率是纵向受力钢筋截面面积As与截面有效面积的百分比。构件的破坏特征取决于配筋率、混凝土的强度等级、截面形式等诸多因素，其中配筋率的影响最大。配筋率不同，受弯构件破坏形式不同。当构件的配筋率超过一定值时，构件的破坏是由于混凝土被压碎而引起的。图3.10受弯构件正截面破坏形态综上所述，受弯构件的破坏是受拉钢筋和受压混凝土相互抗衡的结果。......
2023-09-19
相关推荐