基本公式应用-混凝土结构设计计算

2023-09-19 理论教育版权反馈

【摘要】：c.若2a′s＜x≤ξbh0，则可求得As：已知梁的截面尺寸为b×h=200 mm×500 mm，混凝土强度等级为C40，ft=1.71 N/mm2，fc=19.1 N/mm2，钢筋采用HRB335，即Ⅱ级钢筋，fy=300 N/mm2，受压区已配置3根20 mm钢筋，A′s=941 mm2，截面弯矩设计值M=330 kN·m。将以上有关数值代入基本公式，可得：可见，满足基本公式的适用条件。将x值代入基本公式得：由于M=90 kN·m＜Mu=154.71 kN·m，故此梁安全。

1)截面设计

设计双筋梁时，常遇到如下两种情况：

①已知截面尺寸b×h，弯矩设计值M，材料强度fc、fy，求受压钢筋和受拉钢筋截面面积A′s及As。

解法：为了节约钢筋，应充分发挥混凝土的受压能力，可令ξ=ξb，则x=ξbh0。这样利用公式(3.16)可得到：

若A′s≤0，说明不需设置受压受力筋，可按单筋梁计算。

若A′s＞0，则：

②已知截面尺寸b×h，弯矩设计值M，材料强度fc、fy及所配受压钢筋面积A′s，求受拉钢筋截面积As。

解法：A′s已知，可由(3.17)式求得：

若αs≤0，则：

若αs＞0，可查表得ξ或由公式计算：ξ=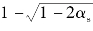 ，可计算出：x=ξh0。

此时，x可能出现3种情况：

a.若x≤2a′s，假定x=2a′s，由(3.16)式求得受拉钢筋As：

b.若x＞ξbh0，说明受压钢筋A′s太少，应按A′s未知，重新计算A′s及As。

c.若2a′s＜x≤ξbh0，则可求得As：

【例3.4】　已知梁的截面尺寸为b×h=200 mm×500 mm，混凝土强度等级为C40，ft=1.71 N/mm2，fc=19.1 N/mm2，钢筋采用HRB335，即Ⅱ级钢筋，fy=300 N/mm2，受压区已配置3根 pagenumber_ebook=60,pagenumber_book=54 20 mm钢筋，A′s=941 mm2，截面弯矩设计值M=330 kN·m。环境类别为一类。求受拉钢筋面积As。

【解】　M′=f′yA′s(h0-a′)=300×941×(440-35)≈114.3×106(kN·m)

则：

按单筋矩形截面求As1。设as=60 mm、h0=500-60=440(mm)。

故满足适用条件。

最后得：

故选用6 pagenumber_ebook=60,pagenumber_book=54 25 mm钢筋，As=2945.9 mm2。

2)承载力校核

已知截面尺寸b×h，材料强度fc、fy，配置钢筋A′s及As，求梁能承受的最大设计弯矩值。

解法：首先可由式(3.15)求出x：

此时，x可能出现如下3种情况：

①若x≤2a′s，则：

②x＞ξbh0，则：

③若2a′s≤x≤ξbh0，则：

计算出的Mu即为截面能承受的最大弯矩。当M≤Mu时，则截面是安全的。

【例3.5】　已知梁截面尺寸b=200 mm，h=400 mm，混凝土强度等级为C30，fc=14.3 N/mm2，钢筋采用HRB400级，fy=360 N/mm2，环境类别为二类b，受拉钢筋采用3 pagenumber_ebook=61,pagenumber_book=55 25(As=1473 mm2)，受压钢筋为216(A′s=402 mm2)，要求承受的弯矩设计值M=90 kN·m，验算此梁是否安全。

【解】　查表或计算得：α1=1.0，fc=14.3 N/mm2，fy=f′y=360 N/mm2，ξb=0.518，混凝土保护层最小厚度为35 mm，故as=35+25/2=47.5(mm)，a′s=35+16/2=43(mm)，h0=400-47.5=352.5(mm)。

将以上有关数值代入基本公式，可得：

可见，满足基本公式的适用条件。

将x值代入基本公式得：

由于M=90 kN·m＜Mu=154.71 kN·m，故此梁安全。

基本公式应用-混凝土结构设计计算

相关推荐