当能够确定勘察区地下水在开采条件下的各项均衡要素时,宜采用水均衡法确定允许开采量。......
2023-09-18
地下水的允许开采量是指在水源地设计的开采时期内,以合理的技术经济开采方案,在不引起开采条件恶化和环境地质问题的前提下,单位时间内可以从含水层中取出的最大水量。
1.开采抽水法
开采抽水法就是在水源地内,按开采条件(开采降深和开采量)进行较长时期(几个月,最好在旱季)的抽水试验。然后根据抽水试验的结果来确定允许开采量。
抽水试验的结果可能出现两种情况:稳定状态和非稳定状态。
(1)稳定状态。按设计需水量进行长时间抽水,最终主井和观测井内的动水位都能在允许的降深范围内保持稳定![]() ,停抽后各井水位又都能较快地恢复到原始水位。根据(GB 50027—2001)《供水水文地质勘察规范》第9.4.6条的规定,当需水量不大,且地下水有充足补给时,可把取水构筑物的总出水量当作允许出水量。因此,当抽水试验的结果为稳定状态,抽水井又已达到极限抽水能力(即达到水井的允许抽水量)时,Q允=Q抽。
,停抽后各井水位又都能较快地恢复到原始水位。根据(GB 50027—2001)《供水水文地质勘察规范》第9.4.6条的规定,当需水量不大,且地下水有充足补给时,可把取水构筑物的总出水量当作允许出水量。因此,当抽水试验的结果为稳定状态,抽水井又已达到极限抽水能力(即达到水井的允许抽水量)时,Q允=Q抽。
(2)非稳定状态。按设计需水量长时间进行抽水,但最终井水位达不到稳定,特别是观测孔中的水位一直在持续下降![]() ;停抽后水位虽有所恢复,但始终达不到原始水位。说明所抽的水量已大于补给量,消耗了含水层的储存量,按这样的抽水量开采是没有保证的。因此,在非稳定状态的抽水情况下,可把开采条件下的补给量作为允许开采量,即Q允=Q补[8]。
;停抽后水位虽有所恢复,但始终达不到原始水位。说明所抽的水量已大于补给量,消耗了含水层的储存量,按这样的抽水量开采是没有保证的。因此,在非稳定状态的抽水情况下,可把开采条件下的补给量作为允许开采量,即Q允=Q补[8]。
在非稳定抽水状态下,抽水初期主井的水位下降很快,随即趋于稳定,而观测井中水位仍持续下降,降落漏斗仍在扩展。在抽水后期,出现主井与观测井的水位同步等幅下降。这时设任一时段Δt的抽水所产生水位下降为ΔS,这时据水均衡关系[8]有:
潜水: (Q抽-Q补)Δt=μFΔS
承压水: (Q抽-Q补)Δt=μ*FΔS
则![]()
或![]()
式中:Q抽为抽水量,m3/d;Q补为开采条件下的补给量,m3/d;ΔS为在Δt时段中的水位下降值(正值),m;μF(或μ*F)为潜水(或承压水)水位下降1m时消耗的储存量,m2;μ和μ*分别为潜水含水层的给水度或储水系数;F为降落漏斗的面积,m2。
可把抽水试验中不同的抽水量和相应的水位降深分别代入式(附3-1),得到系列方程式,然后联立求解,求出μF(或μ*F),再利用式(附3-1)求得补给量Q补。
【实例】 某水源地位于基岩裂隙水的富水地段(潜水)。在水源地的3个孔中进行四个月的抽水实验(各井之间距离超过300m),观测数据见附表3-1。求该水源地的允许开采量Q允。
附表3-1 抽水试验观测资料(据 房佩贤,1987)

解:表中数据显示,抽水试验分两个阶段进行。第一阶段为5月1日—6月2日;在暂停4天后,进行第二阶段抽水(6月7日—6月30日)。虽然每个阶段的抽水量均逐步减小,但水位降深都在增大,表明在抽水试验过程中降落漏斗都随抽水时间的延长逐步扩大,抽水呈不稳定状态。
把表中数据代入式(附3-1)得下面5个方程式[8]:
①3169=Q补+0.47μF;②2773=Q补+0.09μF;③3262=Q补+0.94μF;
④3071=Q补+0.54μF;⑤2804=Q补+0.19μF。
为了减少误差,把5个方程搭配联解,分别求出Q补和μF。结果见附表3-2。
附表3-2 方程搭配联解结果(据 房佩贤,1987)

从计算结果看,不同时段组合所求出的补给量相差不大,但μF值变化较大,可能是裂隙发育不均匀(各段μ差异大),降落漏斗扩展速度不均匀(各抽水期F增速不等)所致。
2.水位恢复法
当抽水完全停止或只进行少量抽水(即当Q抽=0,或Q抽<Q补)时,地下水位在获得外围的补给后得以缓慢上升。根据质量守恒,有[8]:

即
补给量=抽水量+含水层储蓄量的变化
式(附3-2)中,ΔS为含水层在Δt时段内的水位升幅(正值);其他各项意义同前。
据此,可以求出水源地的允许开采量Q允(非稳定状态下的补给量就是允许开采量)。
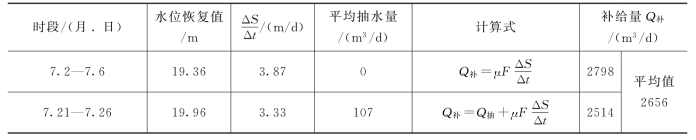
如上述实例中,根据其水位恢复资料也可求出该水源地的补给量,见附表3-3。
附表3-3 水位恢复观测资料(据 房佩贤,1987)
3.相关曲线外推法
相关曲线外推法就是先建立开采量Q-水位降深S之间的相关方程,再根据其相关方程外推未来在设计降深时的开采量。这种做法没有考虑水源地的外围是否存在补给潜力,只适用于抽水量小于补给量的稳定开采状态(因为在非稳定开采状态下,开采量超过了水源地的补给量,也就是超过了水源地的允许开采量)。
根据经验,Q-S的关系大体呈以下四种情况[1]。
(1)直线型。分两种情况:
1)当Q和S的关系为通过原点的直线时,表达式为:
![]()
根据最小二乘法原理,方程中参数q由抽水试验资料,利用下式求得[7]:

2)当Q和S的关系为不通过原点的直线时,表达式为:
S=a+bQ
根据最小二乘法原理,方程中系数a、b求得[8]:

相关系数为: 
(2)抛物线型。表达式为:
S=aQ+bQ2
根据最小二乘法原理,方程中参数a、b由下式求得[7]:
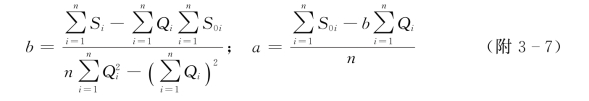
其中

(3)幂函数型。表达式为:
Q=aS1/b
根据最小二乘法原理,方程中参数a、b由下式求得[7]:
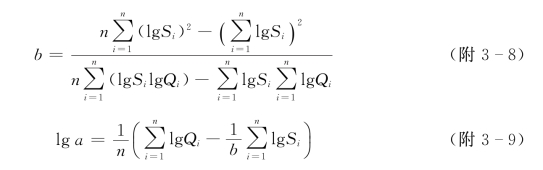
(4)对数型。表达式为:
Q=a+b lg Si
根据最小二乘法原理,方程中参数a、b由下式求得[7]:
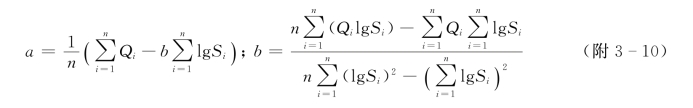
【实例】 某水源地已有多年的开采资料(附表3-4),现要求外推设计降深为26m时的开采量。
解:根据散点图,初步推测Q-S的关系为直线或幂函数关系。现进行这两种相关关系的试算[8]。
(1)直线关系计算。表格计算见附表3-4。
附表3-4 直线相关关系计算表(据 房佩贤,1987)

根据式(附3-6),其相关系数为[8]:

回归方程中的系数a、b为:
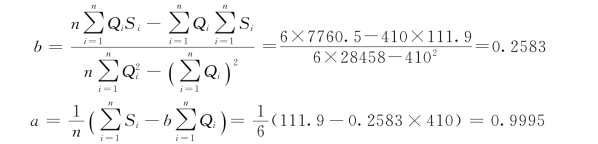
则该回归方程为: S=a+bQ=0.9995+0.2583Q
或: Q=3.87S-3.87
(2)幂函数关系计算。表格计算见附表3-5。
附表3-5 幂函数关系计算表(据 房佩贤,1987)
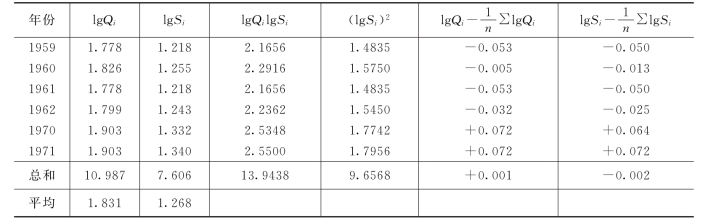
据式(附3-8)、式(附3-9),方程中的系数为:
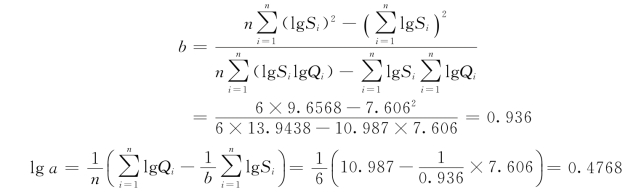
相关系数为[8]:
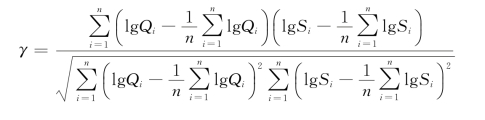
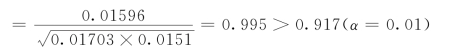
则该相关方程为: Q=aS1/b=2.998S1.0684
(3)外推进行预测。这两个方程的相关系数都很大,均超过了显著水平的最小值,因此均可用来预报地下水的未来开采量。利用这两个方程外推预测设计降深(26m)时的开采量如下:
直线相关法:Q=3.87S-3.87=96.75×104(m3/d)
幂函数相关法:Q=2.998S1.0684=2.998×261.0684=97.41×104(m3/d)
这两种方法预测的结果十分接近。不过,由于直线方程的相关系数较大些,它的预测结果应与实际更接近,实践也证明了这一点。
最后需要提醒的是,利用Q-S关系外推法求地下水的允许开采量没有考虑到扩大开采时的补给因素是否增加,若扩大开采补给不足时,仅根据相关关系预测是有问题的,所以在预测时还应进一步验证相应的补给量。
练习题
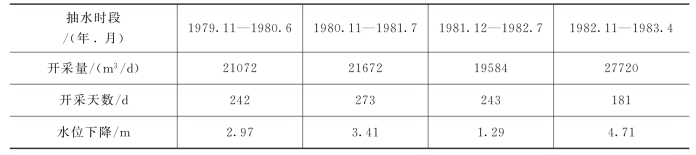
1.在某岩溶水水源地30m×15m范围内集中建井8口,单井出水量可达300~500m3/h。该水源地自1979年投产以来,每天坚持观测主井的水位和水量,同时利用周围矿井观测记录水位变化情况。前四年的观测结果(见附表3-6)表明,在水源地影响范围内,主井和观测井的水位随抽水量和降水季节呈周期性的同步等幅变化。试根据1980年11月—1981年7月和1981年12月—1982年7月的开采资料确定水源地的μF值,然后确定该水源地的允许开采量Q允,并利用水位恢复法(数据见附表3-7)对计算的结果(Q允)予以验证。
附表3-6 抽水引起的水位下降观测资料(据 余正元,2001)
附表3-7 水位恢复观测资料(据 余正元,2001)

2.某水源地开采过程中曾进行数次观测工作,其中5次的资料列于附表3-8。请建立水位降与开采量的相关方程,并利用外推法预测设计水位降深分别为20m、25m时的开采量。
附表3-8 观测数据(据 房佩贤,1987)

有关水文地质勘察(第2版)的文章

在该标准中,将地下水的允许开采量分为A、B、C、D、E五级。要求水源地经过勘探和具有3年以上连续开采的水位、开采量、水质动态的观测资料,以及1∶1万或1∶2.5万的水源地水文地质图。在水文地质条件复杂而且需水量接近允许开采量的情况下,进行过大流量的、长时间的群井开采试验。水文地质图的比例尺分别为1∶20万和1∶5万。E级允许开采量是大面积的区域水文地质调查报告估计的地下水资源量。......
2023-09-18

对地下水资源的分类目前尚未取得统一和完善,有待进一步研究解决。据GB/T 14157—93,地下水资源为含水层中具有利用价值的地下水水量。按GB/T 14157—93规定,地下水天然资源是指天然条件下,地下水在循环交替过程中,可以得到恢复的那部分水量,即多年平均补给量。依据GB/T 14157—93,地下水开采资源是指在一定的技术经济条件下,在不至于引起严重环境地质问题的前提下,单位时间内可从含水层中提取的地下水量。......
2023-09-18

迄今中国已能自行设计、生产了一系列用于空气钻进的钻机及配套机具和若干井内用泡沫剂,如能钻300m和600m的钻机、空气潜孔锤、气举反循环、跟套管钻进、中心取样钻进用的设备、管材、钻头等绝大部分实现了国产化,并有部分出口[5]。......
2023-09-18

通过走访当地群众作调查并作详细的记录。对于地下水已被开发利用的地区,要采取访问与调查相结合进行机井和民井的调查,并根据精度要求,选择有代表性的机井、民井标在图上。......
2023-09-18

地下水动态与均衡的研究,对发展水文地质的基本理论和解决生产实际问题都有着重要意义。没有地下水动态与均衡的研究就不能全面和深入地阐明研究区的水文地质条件,也不能可靠地评价研究区的水质和水量。因此,在各种目的的水文地质勘探中,都规定进行一定时期的地下水长期观测,以便进行地下水动态与均衡的研究。近年来,国内外对地下水动态均衡的研究都很重视,发展迅速。......
2023-09-18
相关推荐