为此需绘制ξ-Q曲线，求出A值，则渗透系数K可按下列公式求出：承压水完整井潜水完整井2.5.1.3利用多孔稳定抽水试验资料计算渗透系数此方法需要两个以上的观测孔资料，具体方法如下：整理多孔抽水试验资料，绘制s-lgr曲线，如图2-24所示。......
2023-09-23
非稳定流抽水试验资料整理与降深比值法分析
【摘要】：利用非稳定抽水试验资料求水文地质参数,可用配线法、雅柯布半对数直线图解法、降深比值法等。导水系数:如含水层为潜水,则给水度:如含水层为承压水,则储水系数:最后取平均值:3.计算实例现有非稳定流抽水试验资料,潜水井的抽水量为2718m3/d。附表1-2试算过程表附表1-3抽水试验资料因此得:u2=0.0019。
利用非稳定抽水试验资料求水文地质参数,可用(泰斯标准曲线)配线法、雅柯布半对数直线图解法、降深比值法等。其中前两者基本上都是利用作图法来求解参数,其方法在相关教材中(地下水动力学或地下水文学)已作详细的介绍,不再赘述。这里仅介绍降深比值法。该方法简单易行,在资料严重不足时(仅需两个时刻的降深数据即可)就能估求参数。
1.降深方法的原理
在做非稳定流抽水试验时,同一观测孔中两个不同时刻t1、t2所观测的水位降深分别为S1、S2,相应时刻的积分参数为u1、u2。
根据泰斯式可分别列出以下两式[1]:
上两式中:μ为给水度;μ*为储水系数。
设以上两式的比值为α,则
若规定S1＜S2,则
α＜1,W(u1)＜W(u2)
由井函数的性质可推知
u1＞u2
假设u1/u2=A(A＞1),则
所以
或
如利用两个观测孔的资料,则
或
将式(附1-4)代入式(附1-3),得:
2.资料整理的步骤[1]
(1)根据选定的两个时刻t1、t2的抽水试验资料,利用式(附1-5)或式(附1-6)、式(附1-3)计算出相应的A值和α值。
(2)根据算出的A、α值,利用α-u2的关系曲线(或试算法)反查出u2值。再按式(附1-4)求出u1值。
(3)将u1、u2值分别代入泰斯公式[式(附1-1)、式(附1-2)],即可计算
参数。
导水系数: 
如含水层为潜水,则给水度:
如含水层为承压水,则储水系数:
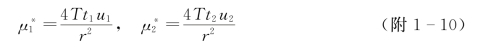
最后取平均值:
3.计算实例
现有非稳定流抽水试验资料(附表1-3),潜水井的抽水量为2718m3/d。观测孔2个,编号分别为B1、B2。试根据该抽水资料求水文地质参数。
解:先用同一孔不同时刻的降深求解。
(1)选用B1孔资料计算[2]。现选用t1=60min,t2=120min。据附表1-3,与这两个时刻对应的B1孔的降深分别为:
S1=0.878m,S2=1.000m
由式(附1-5)得: A=t2/t1=120/60=2
由式(附1-3)得: α=S1/S2=0.878/1.00=0.878
根据A、α值,由试算表(附表1-2)求得u2值。
在试算中,先假定u2=0.01和0.001,查附表1-1分别得到W(Au2)和W(u2)的值,发现其比值α=W(Au2)/W(u2)随着u2的增大而变小。由于真实的α值(0.878)在这两个比值之间,可以断定,所要求的u2值应在0.01～0.001之间。为此,再次假定u2=0.005,经试算后再次断定,真实的u2应在0.001～0.005之间。如此经过反复试算发现,当u2=0.0019时,α=W(Au2)/W(u2)的比值很接近真实值(0.878)。
附表1-1 与u对应的W(u)的值
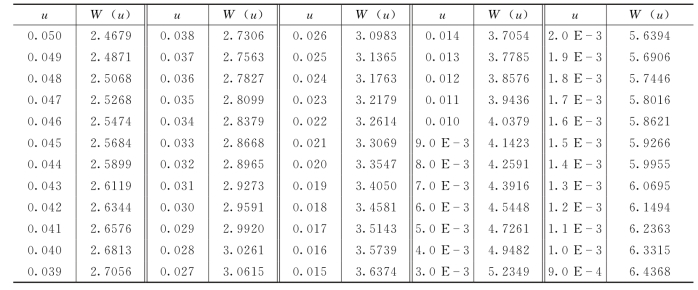
注 本表范围以外的数据可据文献[3],利用表达式W(u)=18.109u0.256-31.370u0.16+13.482近似求出。
附表1-2 试算过程表
附表1-3 抽水试验资料(摘自 李炳森,2005)
因此得:u2=0.0019。由式(附1-4)求得:
u1=Au2=2×0.0019=0.0038
由试算表(附表1-2)得:
W(u1)=4.9993;W(u2)=5.6906
由式(附1-4)求出:
u1=Au2=2×0.0019=0.0038
于是,由式(附1-8)可求出导水系数为[2]:
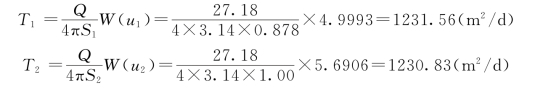
所以
T=(T1+T2)/2=(1231.56+1230.83)/2=1231.20(m2/d)
由式(附1-9)又求得给水度[2]:
则
μ=(μ1+μ2)/2=2.098×10-4
(2)若用B2孔的资料求参。选t1=60min,t2=120min;则相应的降深为:
S1=0.402m,S2=0.518m
仿照以上步骤分别求得[2]:
A=2,α=0.7761,u2=0.03,u1=0.06;
W(u1)=2.2953,W(u2)=2.9591
T1=1234.96m2/d,T2=1234.58m2/d
μ1=2.077×10-4,μ2=2.078×10-4
(3)如同时用B1和B2孔的资料求参。方法如下:
选B1孔:t1=1min,S1=0.201m
选B2孔:t2=80min,S2=0.454m
由式(附1-6b)得[2]:
由式(附1-3)得:
利用两个观测孔资料时的计算过程见附表1-4。
附表1-4 利用两个观测孔资料时的试算过程表
由附表1-4可见,当u2=0.044时,可使α=W(Au2)/W(u2)=0.442,故取u2=0.044。再由式(附1-4)求出:
u1=Au2=5×0.044=0.22
据试算表查得,当u2=0.044时,W(u1)=1.1454,W(u2)=2.5899。由式(附1-8)得导水系数T为:T1=1234.54m2/d,T2=1233.86m2/d。由式(附1-9)得:μ1=2.027×10-4,μ2=2.029×10-4。
根据以上三次计算结果[2]:
导水系数T=1230.83～1235.58m2/d,平均值为1233.21m2/d。
给水度μ=2.027×10-4～2.098×10-4,平均值为2.063×10-4。
此结果与用泰斯标准曲线配线法得计算的结果(T=1272.77m2/d,μ=2.063×10-4)基本一致[2]。
练习题
从附表1-3中随机挑出另两个时段数据,按照文中介绍的步骤和公式,再次计算该含水层的导水系数T和给水度μ。
有关水文地质勘察（第2版）的文章
- 详细阅读
- 详细阅读
-
工程地下水：利用多孔稳定流抽水试验资料计算影详细阅读
影响半径是利用单井抽水试验资料计算含水层渗透系数的原始数据之一。利用稳定流抽水试验资料求影响半径必须有观测孔中的水位下降资料，其求法有两种。......
2023-09-23
-
试验资料整理方法及标准图表优化详细阅读
试验资料整理包括校核原始记录、绘制p-Q曲线、确定p-Q曲线类型、绘制稳压阶段透水率-时间关系曲线。劈裂型和非劈裂型又可进一步细分，见图3.3；p-Q曲线特征描述见表3.2。图3.3高压压水p-Q曲线类型表3.2高压压水p-Q曲线特征表A型p-Q曲线表明当压水压力小于某一数值（拐点）时，岩体的渗透性较弱；压水压力一旦超过拐点压力后，渗透性急剧增加，岩体发生明显的劈裂，拐点处压力可确定为劈裂压力。......
2023-06-28
-
水文地质勘察（第2版）：试验资料整理成果详细阅读
在整个试验期间,裂隙状态基本没有发生变化。该曲线揭示,试验期间裂隙状态发生了变化,岩体渗透性减小,这种减小大多是由于裂隙部分被堵塞造成的。......
2023-09-18
-
地下水抽水试验数据采集与分析-工程地下水详细阅读
图2-46试验场地抽水井和观测井平面布置抽水试验现场工作要求：①各班人员必须严格职责，不得擅自离开岗位，需按时精确量测水位和水量。绘制抽水试验综合成果图。应用稳定流法和非稳定流法求含水层水文地质参数。表2-30含水层水文地质参数汇总......
2023-09-23
- 详细阅读
-
水文地质勘察抽水试验适用条件详细阅读
利用抽水试验所求的渗透系数,代表的是抽水降落漏斗范围内的岩土层的平均渗透性。另外,若有观测孔的多孔抽水试验,所求得的水文地质参数也比较准确。只有在无法利用抽水试验的场合,才选用其他办法。由于包气带内没有地下水可抽,无法采用抽水试验求参。 某承压含水层内,抽水井的井径为300mm,进行单孔稳定流抽水试验,当抽水量为1000m3/d时井内的稳定水位降深为15m。 某潜水完整井进行单孔抽水试验,井径200mm,初始水位埋深2.0m,隔水底板埋深10m。......
2023-09-18
相关推荐