10.5.3.2 拟建渠道的水文地质勘察根据SL 373—2007《水利水电工程水文地质勘察规范》的规定,拟建渠道水文地质勘察的目的、任务和内容如下[54]。......
2023-09-18
11.6.6.1 应用条件
随着电子计算机的出现,在解决复杂水文地质问题时,可以借助数值模拟方法,在电子计算机上用离散化方法求解数学模型的数值解,用数值的集合达到近似的“仿真”[102]。
矿坑涌水量数值计算,其原理方法虽与供水水资源评价完全一致,但由于矿床所处自然环境复杂,开采条件变化大,不确定因素多,又要求作大降深下推预测。因此,矿坑涌水量数值计算的最大特点是:模型识别的条件差、任务重、难度大。不仅要为原始状态下水文地质模型的各项未知条件与不确定因素通过定量化过程得到识别与校正,同时,还要为大降深数值预测建立内边界的互动识别。
11.6.6.2 计算方法与步骤
1.数学模型的选择
数学模型的建立,既要考虑需要,又要分析实际问题的复杂程度是否具有所选模型相应的资料。一般来说,平面二维数学模型已能满足解决实际问题的基本要求,对于在垂向上具明显非均质特征的巨厚含水层,在较大降深的开采量和水位预报时,为避免失真最好采用三维流数学模型[104]。
2.水文地质条件的概化
水文地质条件概化是数值计算中的一个重要环节,要求根据勘探资料,按数值方法对实际问题的特点进行概化。它反映了勘探信息的利用率和保证率,以及对水文地质条件的研究程度直接关系计算精度。数值计算的水文地质条件概化,可概化为结构、边界、流态和初始条件等几大问题[104]。
(1)概化的原则。自然界中含水层的分布组合极其复杂,水文地质条件的概化有较大难度,确定时应遵循三个基本原则:①实用性:所建立的水文地质概念模型必须与一定时期的科学技术以及水文地质调查研究程度相适应,并能用于解决矿坑涌水量预测这一实际课题;②完整性:概念模型要尽可能真实地反映实体系统的内部结构与动态特征,这就要求专业人员既要到现场进行调查,又要广泛地收集与矿山相关的各种信息,必要时还要补充部分现场调查(包括观测、试验等)工作,以达到对真实系统全面深入的掌握,保证模型在理论上的完整性;③正确处理好简单与精度的矛盾,若一味追求简单,那就以牺牲精神度为代价,若一味追求精度,则将导致模型复杂化,将需花更多的时间和勘察成本,故应根据需要将二者协调好。
(2)含水层结构的概化。含水层结构的概化包括含水层的空间形态与结构参数分区的概化。含水层的空间形态的概化,是利用含水层顶、底板标高等值线图,给出每一剖分节点(离散点)坐标(x,y)上的含水层顶、底板标高,由模型自动识别含水层的厚度,完成几何形态的概化。含水层的非均质结构参数分区的概化,是在水文地质分区的基础上,按水文地质条件的宏观规律和渗流运动的特点,在空间上渐变地进行参数分区及参数分级,给出各分区参数的平均值及其上、下限,作为模型调试的依据[96]。对取水含水层与相邻含水层相互作用概化,一般要求地质模型给出与相邻含水层的连接位置与坐标,其连接方式可以是断层、“天窗”或通过弱透水层的越流补给。
(3)地下水流态的概化。流态问题的概化,一般认为在矿区局部存在的一些复杂水流状态但分布范围不大时,因此在宏观上仍可考虑用二维达西流进行概化,也可以根据实际情况概化为“三维流”。
(4)边界条件的概化。边界条件概化时,要求根据边界分布的空间形态,给出边界的坐标,确定边界作用的性质,有无水量交换及其交换方式,并根据动态观测或抽水试验资料,用数理统计方法概化水位或流量的变化规律,按不同时段给出边界节点的水位或单宽流量。
(5)初始条件的概化。按初始时刻各控制节点实测水位资料绘制的等水位线图,给出各节点的水位作为初始条件。由于控制节点的数量有限,等水位线图的制作难免存在一定的随意性,在含水层结构或边界条件较复杂的情况下,最好利用模型的小步长运行,进行校正[104]。
3.计算区域和时间的离散
数值法根据分割近似原理,将一个反映实际渗流场的光滑连续的水头曲面,用一个由若干彼此无缝衔接且不重叠的三角形(有限元法)或方形、矩形(有限差分法)拼凑成的连续但不光滑的水头折面代替,将非线性问题简化为线性问题求解。
时间的离散是根据地下水位降(升)变化的特点,选好合适的时间步长控制水头变化规律,既保证计算精度,又节约运算时间。如模拟抽水试验时,抽水初水位下降迅速,必须用以“分”为单位的小步长才能控制;随着水位降速的变慢,逐渐延长至以“时”“日”为单位的步长;模拟稳定开采时,可用月、季、甚至年为单位的大步长。
4.模型的识别与检验
模型识别是用实测水头值及其他已知条件校正模型方程、结构参数、边界条件中的某些不确切的成分(数学运算中称解逆问题)。根据详勘要求的一个水文年动态观测资料,提供枯、平、丰水季节的天然流场资料和抽水实验的人工流场资料,选用或自编相应的程序软件进行的。模型识别的方法有直接解法和间接解法两种。
5.矿坑涌水量数值预测
模型的预测,通常是在水文地质模型定量化的基础上,按开采方案(即已知疏干工程的内边界条件)预测未来开采条件下外边界的变化规律,从而达到预测的目的。
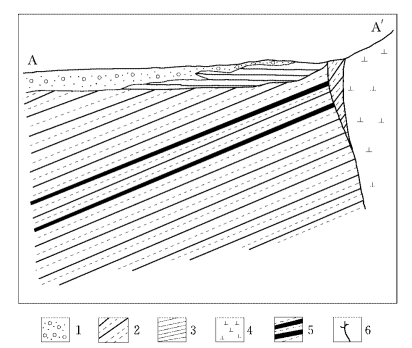
图11-29 双阳煤矿水文地质剖面图(据 刘启仁,1995)
1—砂砾岩;2—砂岩;3—黏土;4—花岗片麻岩;5—煤层;6—断层
用数值法预测矿坑涌水量,其优势是极明显的,它除了能较真实地刻画矿区的水文地质条件外,还能反映出各种复杂的开采条件与各种类型及强度的疏干工程,模拟疏干过程,反映预报区内疏干条件下各种水文地质条件的变化(如局部范围内含水层由承压转无压到疏干),以及疏干对天然排泄点和供水水源地的水量袭夺,疏干矿井之间的相互袭夺过程等,因此它能根据不同水文地质条件和不同生产要求作出相应的预报,实现包括解析法在内的传统计算方法难以实现的目的。
11.6.6.3 实例
三维数值模型在双阳煤矿巨厚多层含水层矿坑涌水量预测中的应用[12]。
1.区域水文地质条件概述
双阳煤矿位于双鸭山盆地的东侧,基底为元古界麻山群变质岩。四周相对封闭,西部有一条河(七星河),整个煤系地层为一单斜构造(图11-29)。
矿区上覆第四厚层(平均厚度50m)孔隙含水层,下覆侏罗系巨厚(约650m)裂隙含水层,自上而下,裂隙发育由强至弱,具明显非均质性,中间夹有非连续黏土层(厚度为0~25m)(图11-30)。因此,确定侏罗系裂隙含水介质在垂向上的不均匀性及其与上覆第四系孔隙含水层的水力联系,是保证预测精度的关键。
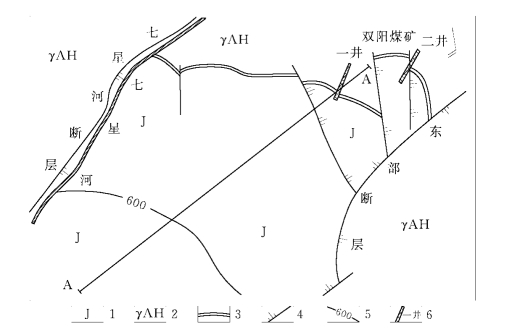
图11-30 双阳煤矿水文地质简图(据 刘启仁,1995修改)
1—侏罗系;2—麻山群花岗片麻岩;3—地层界线;4—断层;5—侏罗系地层-600m等值线;6—矿井位置及编号
2.数学模型的选择
在上述水文地质条件下,若采用常规“准三维”数值模拟模型,不仅会使模型产生严重“失真”,而且难以保证计算过程的稳定性。
本次预报采用三维数值模拟模型,将研究区作为一个统一的地下水含水系统处理。数学模型如下:
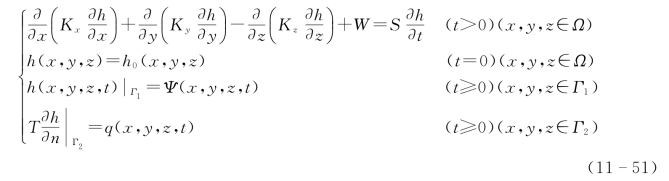
式中:Kx、Ky、Kz为沿三维空间坐标轴方向的渗透系数,[L/T];W为源汇项;S为储水率,[1/L]。
3.水文地质条件的概化
(1)含水层结构概化。根据侏罗系裂隙含水层的非均质性,将其划分为四个含水段。因而,整个区域在剖面上概化为由第四系孔隙含水层和侏罗系裂隙含水层(段)组成的统一的地下水含水系统(图11-29)。
(2)地下水流态的概化:三维达西流。
(3)边界条件概化。平面上:第一层,西部河流为常水头边界,其余均为隔水边界;第二至五层,四周均为隔水边界。垂向上:上部为垂向面状流量边界;底部(侏罗系)为隔水边界。
(4)初始条件。采用1992年6月实测流场数值。求参拟合时间为12年。预测计算时间为10年。时间步长为1年。
4.计算过程(略)
5.计算结果及稳定性分析
(1)计算结果。矿坑涌水量预测结果见表11-18,未来疏干区流场情况如图11-31所示。
表11-18 各疏干区(段)矿坑涌水量预测结果(据 刘启仁,1995修改)

(2)稳定性分析。未来井巷开拓或掘进过程的不确定性将给整个预测过程带来一定的不可预测性。这是否会影响到计算结果?程度如何?
分析结果:图11-32中表示的是两种疏干过程处理方式,A和B的涌水量计算结果表明:疏干过程处理的人为性对A点以后的计算结果影响很小;自第6时段以后预测涌水量值渐趋稳定。因此所得预测结果具有较高的稳定性。

图11-31 3线以西-600~-150m预测疏干流场剖面示意图(剖面Ⅵ)(据 刘启仁,1995)
(注:图中标1、2、…为计算序号;1井、2井表示开采井)
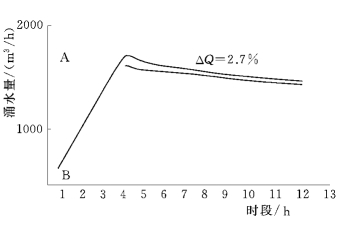
图11-32 三采区-50~+10m对比预测矿坑涌水量历时曲线(据 刘启仁,1995)
A—疏干水位在所有时段均为疏平水平;B—疏干水位分三个时段达到疏干水平
有关水文地质勘察(第2版)的文章

10.5.3.2 拟建渠道的水文地质勘察根据SL 373—2007《水利水电工程水文地质勘察规范》的规定,拟建渠道水文地质勘察的目的、任务和内容如下[54]。......
2023-09-18

迄今中国已能自行设计、生产了一系列用于空气钻进的钻机及配套机具和若干井内用泡沫剂,如能钻300m和600m的钻机、空气潜孔锤、气举反循环、跟套管钻进、中心取样钻进用的设备、管材、钻头等绝大部分实现了国产化,并有部分出口[5]。......
2023-09-18

目前对水库的防渗措施主要有以下方面。根据国内部分已建水库的防渗处理经验,类似条件的渗漏,采用铺设塑料薄膜防渗效果很好,而且省工省时。......
2023-09-18

第二章 水文地质条件①叙述含水层带的空间分布及其水文地质特征;②阐述地下水的补给径流排泄条件及其动态变化规律;③叙述地下水的水化学特征污染现状及其变化规律;④说明拟采含水层带与相邻含水介质及其他水体之间的水力联系状况。......
2023-09-18

对地下水资源的分类目前尚未取得统一和完善,有待进一步研究解决。据GB/T 14157—93,地下水资源为含水层中具有利用价值的地下水水量。按GB/T 14157—93规定,地下水天然资源是指天然条件下,地下水在循环交替过程中,可以得到恢复的那部分水量,即多年平均补给量。依据GB/T 14157—93,地下水开采资源是指在一定的技术经济条件下,在不至于引起严重环境地质问题的前提下,单位时间内可从含水层中提取的地下水量。......
2023-09-18

表5-6渗水试验各方法的装置示意图及其特点5.3.1.1 试坑法试坑法是在表层土中挖一试坑进行的渗水试验。图5-16黏性土中渗水土体浸润部分示意图[5]试坑法常用于测定毛细压力影响不大的砂类土的渗透系数,不适合用于毛细压力影响大的黏性土类。图5-17渗水试验中渗透速度历时曲线图[5]5.3.1.3 双环法双环法是在试坑底嵌入两个铁环,外环直径采用0.5m,内环直径采用0.25m。......
2023-09-18

布孔时,必须考虑工农业供水的要求及当地水文地质条件的研究程度。钻孔的布置应能全面控制地区的地质—水文地质条件。禁止将勘探孔平均布置。例如经过一段钻探工作后,发现某一地段地质、水文地质条件变化不大,而现有的资料已足以阐明其变化规律时,则可适当地削减原设计方案中的勘探工作量。......
2023-09-18
相关推荐