根据地下水动力学原理的解析法解决矿坑涌水量预测问题

11.6.5.1 解析法的原理

解析法是根据地下水动力学原理,利用各种理想化数学模型的解析公式,解决矿坑涌水量预测中的各种实际问题。它既能为疏干设计提供参考数值与指标,又具适应能力强、快速、简便、经济等优点,是最常用的基本方法。

解析法预测矿坑涌水量时,以井流理论和等效原则构造的“大井”为主。“大井”指将各种形态的井巷与坑道系统,以具有等效性的“大井”表示,亦称“大井”法[12]。因此说矿坑涌水量计算的最大特点是“大井”法与等效原则的应用(而供水则以干扰井的计算为主)[5]。其应用范围可分为两个方面。

1.稳定井流解析法

在矿区疏干过程中,当矿坑涌水量及附近水位降深仅随季节变化在一定范围内波动外,均呈相对稳定状态时,即可认为以矿坑为中心形成的地下水渗流场基本符合稳定井流条件。应用于矿坑疏干流场处于相对稳定状态的流量预测,其计算主要包括以下两个方面:

(1)在已知某开采水平最大水位降深条件下的矿坑总涌水量。

(2)在给定某开采水平疏干排水能力的前提下,计算地下水位降深值。

2.非稳定解析法

用于矿床疏干过程中地下水位不断下降,疏干漏斗持续不断扩展的,非稳定状态下的涌水量预测。其计算主要包括以下三个方面:

(1)已知开采水平水位降深(S)、疏干时间(t),求涌水量(Q)。

(2)已知Q、S,求疏干某水平或漏斗扩展到某处的时间(t)。

(3)已知Q、t,求S,以确定漏斗发展的速度和漏斗范围内各点水头值随时间的变化规律,用于规划各项开采措施。

11.6.5.2 应用条件

在解决实际问题时,存在适合解析法的情形常常是不多的,因为描述它的方程式简单,计算区的几何形状规则,定解条件单纯。从地质条件看,这等于对含水层的物理性质与几何特征及其水文地质条件提出了极其苛刻的要求。通常把完全满足这些条件的模型称为理想化模型,但实际问题不可能如此理想。因此,采用解析法预测矿坑涌水时,不可避免地会把复杂的实际问题简化纳入各种理想化的特定模式中。当实际问题与某一理想化模型甚为近似,则解析法的应用既经济又简易快速,但大多数情况下,实际问题与理想化模型之间的差异甚大,因此这种按解析解要求作出的严格理想化处理,常常难免导致失真。

多数情况下,矿坑涌水量预测并不苛求对疏干全过程的定量描述,而只求其正常涌水量与最大涌水量,这就使稳定井流解析公式的应用仍然,具有广泛的实用价值。

11.6.5.3 计算方法

如上所述,应用解析法预测矿坑涌水量时,关键是如何在查清水文地质条件的前提下,将复杂的实际问题按解析公式的“建模”条件理想化,这就是通常所称的矿区水文地质条件的概化。它也是把各种复杂的实际问题,通过建立物理模型(即水文地质模型)抽象为数学问题的过程。它可概括为如下三个重要方面。

1.分析疏干流场的水力特征

矿区的疏干流场是在天然背景条件下,叠加了开采因素演变而成的,分析时,应以天然状态为基础,结合开采条件作出合理概化。其主要任务包括以下几个方面:

(1)区分稳定流与非稳定流。矿山基建阶段,疏干流场的内外边界为受开拓井巷,以消耗含水层储量为主,属非稳定流。进入回采阶段后,井巷轮廓大体已定,疏干流场主要受外边界的补给条件控制,当存在定水头(侧向或越流)补给条件时,矿坑涌水量被侧向补给量或越流量所平衡,流场特征除受气候的季节变化影响外,呈现相对稳定状态。基本符合稳定的“建模”条件,或可以认为两者具等效性,反之,均属非稳定流范畴[98-100]。

在某些矿区的疏干过程中,不仅存在着疏干流场的相对稳定阶段,而且地下水运动的稳定状态与非稳定状态,是随着矿山工程的进展而不断相互转化的,并非彼此无关。

因此,在选用稳定流解析法时要慎重,必须进行水量均衡论证,判断疏干区是否真正存在定水头供水边界或定水头的越流系统。

(2)区分达西流与非达西流。在矿坑涌水量计算时,常遇到非达西流问题,它涉及解析法的应用条件,在宏观上可概括有两种情况:

1)岩溶地下河或岩溶管道岩溶充水矿床,地下水运动为压力管道流与明渠流,此外,分水岭地段的充水矿床,矿坑涌水量直接受垂向入渗降雨强度控制,与水位降深无关。这两情况均与解析法的“建模”条件相距甚大,此时对矿坑涌水量的预测应选择水均衡法或各种随机统计方法。

2)局部状态的非达西流,常发生在大降深疏干井巷附近与某些特殊构造部位,它只对参数计算与参数的代表性产生影响。

(3)区分平面流与空间流。严格讲,在大降深疏干条件下,地下水的垂向运动速度分量是不能忽略的,应为三维空间流(包括非完整井巷的地下水运动),但其分布范围仅限于井巷附近,一般为含水层厚度的1.5～4.75倍。因此,在矿坑涌水量预测中,大多将其纳入二维平面流范畴,在宏观上不影响预测精度。计算时应根据井巷类型作出不同的概化。

如竖井的涌水量计算,可概化为平面径向流问题,以井流公式表达。计算水平巷道涌水时,以剖面平面流近似,采用单宽流量解析公式,但其两端上往往也产生辐射流(图11-17),需要考虑它的存在,并采用平面径向流公式补充计算巷道端部的进水口[6]。

坑道系统则复杂得多,根据“大井”法原理,一般以近似的径向流概化,但当坑道系统近于带状的狭长条形时,也可概化为剖面流问题。

对于倾斜坑道,根据阿勃拉莫夫有关电模拟法的研究,证明坑道的倾斜对涌水量影响不大。可根据坑道的倾斜度,分别按竖井或水平巷道近似,若坑道倾斜度大于45°时,视其与竖井近似,用井流公式计算;若坑道倾斜度小于45°时,则视其与水平巷道近似,用单宽流量公式计算。

根据解析解的存在条件,一些简单的非完整井巷涌水量计算,可以运用三维空间流问题予以解决,此时,可根据非完整井的特点,运用地下水动力学中映射法与分段法的原理来求解。通常用平面分段法解决完整竖井的涌水量计算,用剖面分段法解决非完整平巷的涌水量计算。

(4)区分潜水与承压水。与供水不同,在降压疏干时,往往出现承压水转化为潜水或承压及无压水。此外,在陡倾斜含水层分布的矿区,还可能出现坑道一侧保持原始承压水状态,而另一侧却由承压水转化为无压水或承压及无压水的现象[6](图11 -18)。概化时,需从宏观角度作等效的近似处理。

图11-17　水平巷道周围地下水流态图(据　房佩贤等,1987)

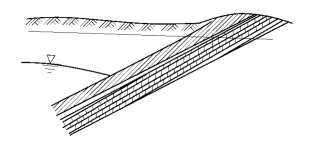
图11-18　某矿区疏干漏斗示意图(据　房佩贤等,1987)

2.边界条件的概化

边界条件概化的失误常常是导致解析解失真的主要原因之一。由于理想化常与实际条件相差甚远,成为解析法应用中的难点,也是解析法预测矿坑涌水量的重要环节。

(1)侧向边界的概化。解析法要求将复杂的边界补给条件概化为隔水与供水两种进水类型,同时,将不规则的边界形态,简化为规则的形态。但实际问题中一般难以具有上述理想条件,其进水条件常常既不完全隔水,又不具有无限补给能力,它的分布也极不规则。须通过合理的概化,缩小理论与实际的差距,满足近似的计算要求。其要点如下:

1)边界条件的概化应从分析解析解的存在条件与矿区水文地质条件入手,立足于矿区水文地质条件概化的整体效果,而不拘泥于局部边界概化的优劣。

2)边界条件概化应从宏观的等效原则出发,通过相对概念寻求近似的途径,达到理论与实际的统一。

3)进水边界类型与几何形态,是边界概化中两个相互制约、不可分割的基本要素,进水类型的概化虽然是关键,但几何形态的概化也需认真对待。如湖北录山铜矿的露天矿涌水量预测。矿坑充水来自围岩大理岩,其与东西两侧岩浆岩隔水层呈30°交角,向南敞开,如图11-19、图11-20所示。20世纪60年代勘探时,概化为东侧直线隔水的环状供水边界,采用非完整井稳定井流法预测矿坑涌水量为5958～7985m3/d,而实际涌水量仅3790m3/d,误差为57%～111%;70年代回访调查验证计算时,采用30°扇形补给边界的稳定流近似计算,得涌水量3685m3/d,实际涌水量为3416m3/d,误差仅7.8%[16],证明边界形态概化的重要性。

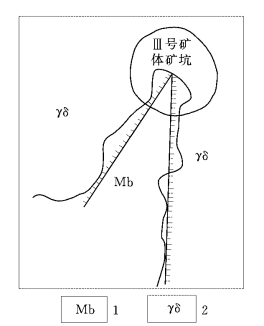
图11-19　录山铜矿大理岩边界示意图(据　录山铜矿,1979)

1—大理岩;2—岩浆岩

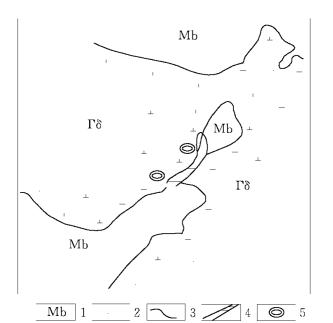
图11-20　录山铜矿矿区边界概化图(据　录山铜矿,1979)

1—大理岩;2—岩浆岩;3—大理岩投影界限;4—65m中段坑道;5—竖井

4)边界条件概化,必须从遵循区域水均衡条件,分析不同疏干条件下边界位置及其进水条件的变化规律。疏干流场始终处于补给量与疏干量不断变化的动平衡状态,随着开采条件的变化,边界的位置及其进水条件常发生转化。如湖南恩口煤矿的东部边界[63],如图11-21所示,在Ⅰ水平疏干时东部壶天河不起作用;开采延伸至Ⅱ水平时,因排水量增大,使漏斗扩展到壶天河,成为茅口灰岩的定水头供水边界;当疏干达到Ⅲ水平时,排水量随降深继续增加,当壶天河的补给能力无法与其平衡时,其定水头供水边界已不复存在,漏斗扩展至由隔水层构造的隔水边界,但壶天河仍以变水头集中补给形式平衡疏干漏斗的发展。

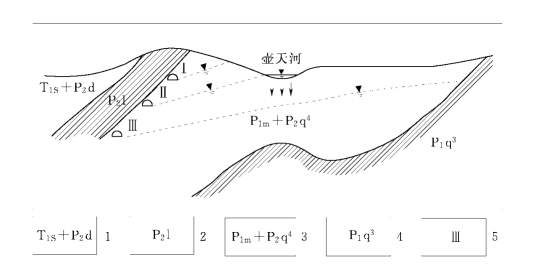
图11-21　恩口矿区边界条件转化示意图(据　曹剑峰等,2006)

1—T1 s+P2 d下叠大冶组;2—P2 l上叠龙潭组隔水层;3—P1 m+P2 q4下二叠茅口组与栖霞组岩溶含水层;4—P1 q3下二叠栖霞组李子塘段隔水层;5—Ⅰ、Ⅱ、Ⅲ疏干水平

5)边界概化应把重点放在主要供水边界上,因为它控制着矿区的水量均衡条件与涌水预测量的精度。孙纳正教授运用数值法与解析法对理想化模型的对比验证计算表明:简化供水边界的形状往往会带来较大的误差,但简化隔水边界的形状影响一般不大[93]。

6)应尽量避免将边界条件置于局部构造部位,这些由局部构造组成的边界,常因疏干漏斗的扩展而导致失效,并被区域均衡边界所替代。

(2)各种类型侧向边界条件下的计算方法。

1)映射法。即根据地下水动力学中的映射叠加原理,获得矿坑涌水量预测所需各种特定边界条件下的解析公式。可采用如下一般形式表示。

稳定流:　

非稳定流:　

式中:RΛ与Rr分别为稳定流与非稳定流的边界类型条件系数。基本的理想化的边界条件系数见表11-14。

2)分区法。也称卡明斯基辐射流法。它是从研究稳定状态下的流网入手,根据疏干流场的边界条件与含水层的非均质性,沿流面和等水压面将其分割为若干条件不同的扇形分流区[5],如图11-22所示。每个扇形分流区内地下水流都呈辐射流,沿水流面分割所得的各扇形区边界为阻水边界,而沿等水压面分割所得的扇形区边界为等水头边界。用卡明斯基平面辐射流公式分别计算各扇形区的涌水量Qi。

表11-14　解析法理想化的边界条件系数表

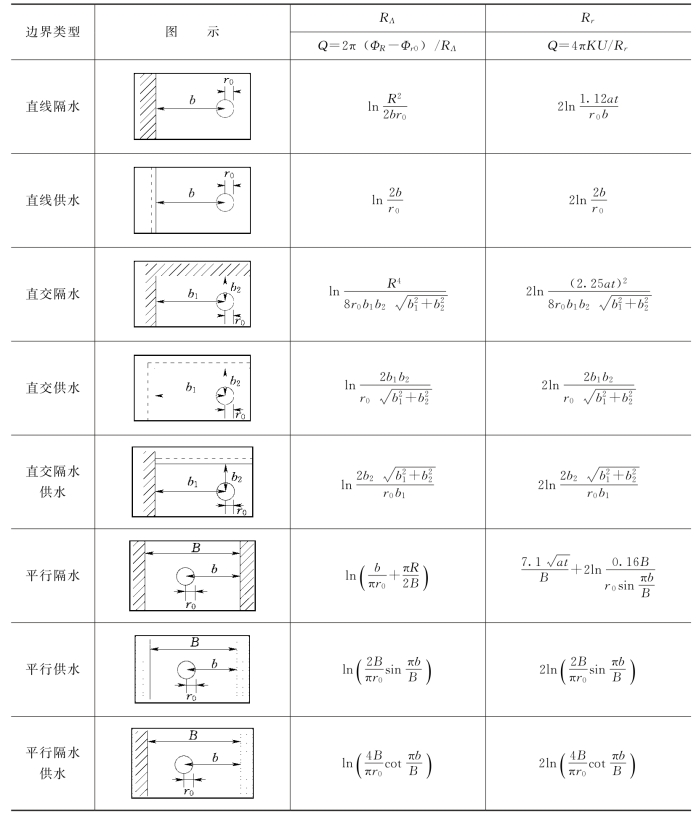
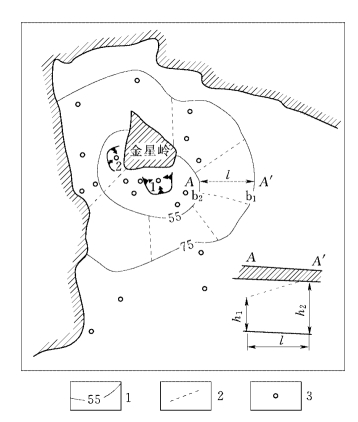
图11-22　某矿区辐射流计算图(据　曹剑峰等,2006)

潜水: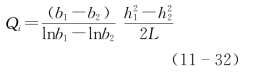

承压水:

式中:b1与b2分别为流区辐射状水流上下游断面的宽度,m;h1与h2分别为b1与b2断面隔水底板上的水头高度,m;L为b1与b2断面的间距,m。

然后,按下式求各分区流量的总和:

每个扇形区内的下游断面,是以直接靠近井巷的疏干漏斗等水头线的一部分为准;而上游断面则以远离井巷的供水边界上等水头线面一部分为准。

(3)垂向越流补给边界类型的确定及其计算。当疏干含水层的顶底板为弱透水层时,其垂向相邻含水层就会通过弱透水层对疏干层产生越流补给,出现所谓的越流补给边界。越流补给边界分定水头和变水头二类,解析法对变水头的研究还尚待解决[91]。

产生定水头垂向越流补给。此时的矿坑涌水量计算,可用增加了越流因数B的形式来表示:

稳定流:　

非稳定流:　

式中:B为越流因数,其表达式可见式(6-19);K0为零阶第二类虚宗量Bessel函数。

3.参数确定

(1)渗透系数的确定。渗透系数是解析公式中的主要参数。中国矿山大多分布于基岩山区的裂隙、岩溶充水矿床,充水含水层的渗透性具明显不均匀性,根据解析计算要求,应作均值概化,同时这也是保证渗透系数具有代表性的措施之一。矿坑涌水量预测中常用的方法有两种。

1)加权平均值法,又可分为厚度平均、面积平均、方向平均法等。如厚度平均法,其公式为:

或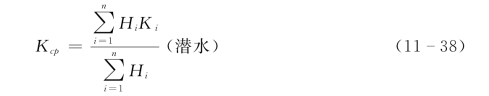

式中:Kcp为渗透系数的加权平均值,m/d;Mi、Hi分别为承压、潜水含水层各垂向分段厚度,m;Ki为相应分段的渗透系数,m/d。

2)流场分析法,有等水位线图时,可采用闭合等值线法:

或据流场特征,采用分区法:

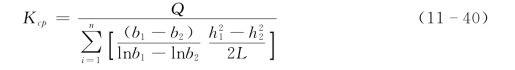
式中:Kcp为渗透系数的加权平均值,m/d;L1、L2为任意两条(上、下游)闭合等水位线的长度,m;Δr为两条闭合等水位线的平均距离,m;Δh为两条闭合等水位线的水位差,m;Mcp为含水层的平均厚度,m;Q为涌水量,m3/d;b1、b2为辐射状水流上、下游断面上的宽度,m;h1、h2为b1和b2断面隔水底板以上的水头高度,m;L为b1和b2断面之间的距离,m。

(2)大井引用半径r0的确定。矿坑的形状极不规则,尤其是坑道(井巷)系统,分布范围大,形状千变万化,构成了复杂的内边界。根据解析法计算模型的特点,要求将它理想化。经观测,坑道系统排水时,其周边逐渐形成了一个统一的降落漏斗。因此,在理论上可将形状复杂的坑道系统看成是一个理想“大井”在工作,此时整个坑道面积,看成是相当于该“大井”的面积。整个坑道系统的涌水量,就相当于“大井”的涌水量。这样就使一般的井流公式,能适应于坑道系统的涌水量计算。这种方法,在矿坑涌水量预测中称为“大井”法。“大井”的引用半径r0,在一般情况下用下式表示:

式中:r0为“大井”引用半径,m;F为坑道系统分布范围所圈定的面积,km2。

如果开采面积近于圆形、方形时,采用上式较准确,对于形状特别的面积,可采用其他专门公式计算。

(3)引用影响半径R0的确定。从稳定井流理论的实际应用出发,即根据等效原则,将疏干量与补给量相平衡时出现的稳定流场,其边界引用一个圆形的等效外边界进行概化,其与“大井”中心的水平距离称为“引用影响半径”,也称为补给半径。则

引用影响半径(R0)=“大井”引用半径(r0)+排水影响半径(R)

矿山疏干实际表明,矿坑排水的影响范围,总是随时间的延长、排水量的增加以及坑道的推进而不断扩大,直至天然边界为止,它不可能被限制在一个不是边界的理想“半径”之内。此外,对比计算表明,若确定影响半径的误差为2～3倍,则矿坑涌水量的计算误差可达30%～60%,若取偏低值其误差远比取偏高值要大[12]。因此,对开拓井巷的涌水量预测,最好采用抽水试验外推法,即根据多落程的抽水试验,确定降深与影响半径或流量与影响半径的线性关系,以外推某疏干水位或某疏干量的相应疏干半径值。如:

式中:R为疏干半径,即排水影响半径,m;S为疏干降深,m;H为含水层厚度,m;K为含水层渗透系数,m/d,此式系经验公式,无需量纲检验。

4.最大疏干水位降深Smax的确定

在理论上,目前解析解还无法处理承压区与无压区同时并存或大降深的潜水问题,实际问题则是矿床疏干时最大可能水位降深是多少,如何近似确定最大疏干水位降深Smax值。

爱尔别尔格尔在实验中取得的潜水最大水位降深等于潜水含水层一半的结论,即Smax=1/2H(扩大应用到承压含水层时,为Smax=H-1/2H),一直是水文地质计算中所遵循的概念。近年来,中国通过渗流槽及野外抽水试验,证明这一结论是保守的[91,92]。Smax可以超过0.8H,在矿坑涌水量计算中,通常不考虑这一概念。据观测,在长期疏干条件下的大截面井巷系统外缘,动水位(h)一般不超过1～2m,它所引起的涌水量计算偏大值一般为0.5%～1%。因此,矿坑涌水量预测时,最大疏干水位降一般取Smax=H。

11.6.5.4 实例

1.实例1

某煤矿的煤层埋藏在二叠系砂岩承压含水层之下,煤系地层被断层切割,断层透水但富水性不强。巷道系统面积1.09m2,其轮廓为不规则的圆形,砂岩含水层平均水头为100m,含水层厚度30m,渗透系数为0.2m/d,巷道系统布置在隔水层底板(图11-23),地层倾角为13°。试预测矿坑涌水量。

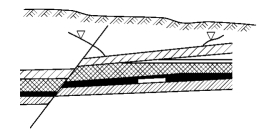
图11-23　某矿区剖面示意图(据　房佩贤等,1987)

根据已知条件,断层能透水则说明其不是隔水边界,但其富水性不强说明其也不是供水边界,因此可视为无限边界。地层倾角13°,可视为水平含水层,含水层的厚度和渗透系数已经概化过。由图可以看出,矿井排水时水位已降至隔水顶板以下,属承压及无压水,因此应选用无限边界承压及无压公式计算矿井涌水量。即

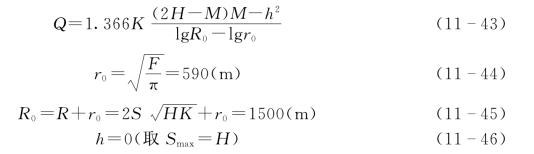
将有关参数代入公式可得:

Q=3666m3/d

实际开采中,矿坑涌水量为3600m3/d,与预测结果接近。

2.实例2

某铁矿地处灰岩区,岩溶裂隙发育较均匀,地下水运动符合达西定律,矿区内有部分地下水动态长期观测资料,其他地质条件略[6]。

(1)要求。

1)当疏干水平(或中段)的水位降深(S)确定后,则疏干量(Q)是时间(t)的函数。该水平的正常疏干量,应是该水平预测的矿坑涌水量值。设计部门要在一组具不同疏干强度Q及与其相应的时间t的对比中,选出最佳疏干方案,即选择排水能力要求不过大,而疏干时间又不长的方案。

2)疏干时间通常要求控制在两个雨季之间,否则Q的计算则无意义。

(2)任务。给定的条件是:①疏干中段水位降(S)确定为0m标高;②疏干时间要求在两个雨季间完成。

(3)最佳疏干量的计算与分析。

第一步:初选疏干时间段t。根据第二项任务,在现有地下水动态曲线(图11-24)上初选3个时间段,即270d、210d、150d,供计算分析。

图11-24　某矿区地下水水位动态曲线图(据　曹剑峰等,2006)

第二步:确定相应的Q值。根据给定的0m标高,从动态曲线图上确定出各时间段相对应的S值(表11-15)。

表11-15　不同时间段S与t的对应 关系(据　曹剑峰等,2006)

第三步:求相应的Q值。利用下面公式(符号为常用地下水动力学符号):

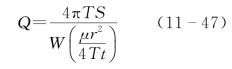
在已知t1、S1、t2、S2、t3、S3的条件下,求得相应的Q1、Q2、Q3,作为第四步分析的初值。

第四步:绘制不同疏干强度Q条件下的S=f(t)曲线(图11-25)。在初值Q1、Q2、Q3的范围内,通过内插给出一组供进一步分析的疏干量数据。其公式为:

分析不同疏干量时S随t的变化规律。

第五步:绘制不同定降深S条件下的S=f(t)曲线。根据图作出不同降深S条件下的疏干量Q与时间t的关系曲线Q=f(t)(图11-26),进行不同S条件下,疏干量Q与疏干时间的对比分析。

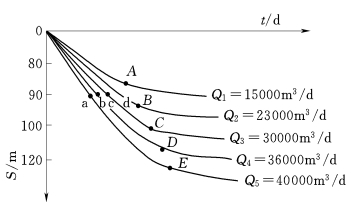
图11-25　不同疏干量条件下S=f(t)曲线(据　曹剑峰等,2006)

图11-26　不同降深条件下Q=f(t)曲线(据　曹剑峰等,2006)

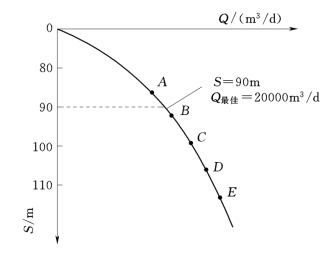
图11-27　拟稳定疏干量与降深的关系曲线(据　房佩贤等,1987)

第六步:绘制降深S与最佳疏干量Q的关系曲线。根据图中各S=f(t)曲线的拐点,求出不同降深S条件下的最佳疏干强度Q,即拟稳定疏干量与降深的关系曲线(图11-27)。

第七步:确定最佳疏干量,并检验其可行性。根据图11-27取得的不同降深的最佳疏干量Qmax检验它们达到S时所需的时间t,是否满足任务要求,即是否能在两个雨季之间完成疏干任务。如符合需要,预测就算完成;如不符合,则还要重复进行,直至所选取的最佳疏干量满足任务要求的S与t时为止。

从图11-26取S=90m,则Q最佳=20000m3/d;从图11-26中求得t=200天;可行性检验:200天＜210天,符合技术要求。

继之,求雨季最大疏干量Qmax:雨季地下水位上升,如以t表示雨季的时段长,以S表示水位上升幅度。为保证开采水平(中段)的正常生产,必须将雨季(特别是丰水年雨季)抬高的水头S降下去。因此,雨季的最大疏干量应为开采水平正常疏干量Q(即正常涌水量),亦即在前面所确定的最佳疏干量,再加雨季t时段抬高S所增加的疏干量,称疏干增量,即

Qmax=Q最佳+Q雨增

上述Qmax计算,关键是雨季t及其时段内地下水位上升幅度的确定。一般按动态观测资料会给出抬高S的平均值,较为可靠。将所得t、S代入式(11-47),则可计算出雨季增加的疏干量Q雨增。

3.实例3

广东曲塘多金属矿位于一个构造盆地边缘,地势平缓,雨量充沛,地表水系发育。矿体位于当地侵蚀基准面以下,赋存于含水性差的上泥盆统天子岭组泥灰岩中。由于地层缺失,在某些地段使强烈岩溶化的中上石炭统壶天群灰岩直接覆盖其上,构成矿区主要充水含水层。此外,地表分布有弱含水的第四系冲积黏土夹砾石[5]。矿区北、西有隔水层,东、南开阔,有地下水与地表水联系密切。根据边界的概化(图11-28)选择直交隔水边界的稳定流“大井”公式,计算各开采中段稳定涌水量,即

图11-28　广东曲塘矿区水文地质示意图(据　房佩贤等,1987)

1—相对隔水边界;2—河流;3—断层;4—上升泉;5—强烈岩溶化灰岩;6—砂页岩、泥灰岩

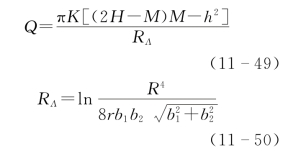
将-40m中段的矿坑涌水量计算的参数和结果列入表11-16和表1-17中。

表11-16　曲塘矿-40m中段矿坑涌水量计算所用参数(据　房佩贤等,1987)

表11-17　曲塘矿-40m中段矿坑涌水量预测计算表(据　房佩贤等,1987)

表11-16中的R=αQ,其中α为比例系数,根据多次水位落程的抽水试验求得。