水文地质勘察：准确估算水库渗漏量

2023-09-18 理论教育版权反馈

【摘要】：由于渗透损失为暂时性渗漏,其水量较小,一般情况下可忽略不计。K按加权法求得[6]:10.1.4.2 绕坝渗漏量Q绕坝的估算绕坝渗漏水流有潜水类型和承压水类型两种,计算方法稍有不同。图10-10单层岩土体分水岭渗漏量计算剖面无坡积层;有坡积层2.单层透水层分水岭、隔水层倾斜时(图10-

水库渗漏可分为坝区渗漏和库区渗漏。其中坝区渗漏又分为坝基渗漏和绕坝渗漏,库区渗漏包含库水的渗透损失和渗漏损失。由于渗透损失为暂时性渗漏,其水量较小,一般情况下可忽略不计。因此,水库的总渗漏量一般是其余三部分之和,即

式中:Q坝区、Q库区分别表示坝区渗漏量、库区渗漏量;Q坝基、Q绕坝、Q库区渗漏分别为坝基渗漏量、绕坝渗漏量和库水的渗漏损失量。

若为渗漏病险的水库,当坝体也出现渗漏时,水库的总渗漏量则为:

在实际工作中,坝体的渗漏量Q坝体可根据实测得到。由于土石坝体内部组成物质高度不均一,以及存在很大的垂向渗流,不宜用动力学公式或数值法估算。

其余的各项渗漏量一般都可采用地下水动力学的公式来估算的,因此,本文对此进行重点介绍。地下水动力学的公式本质上是由达西公式推导出来的,因此其适用的前提条件是地下水是达西流且含水介质为均质各向同性。

10.1.4.1 坝基渗漏量Q坝基的估算

1.单层透水坝基

pagenumber_ebook=219,pagenumber_book=205

当坝基为单层透水层,其厚度等于或小于坝底宽度时,假定坝身不漏水,则可将边界条件进行简化,如图10-5所示,按达西公式求得[6]:式中:q为坝基单宽剖面渗漏量,m3/(d·m);K为透水层渗透系数,m/d;H为坝上下游水位差,m;2b为坝底宽,m;T为透水层厚度,m。

图10-5中,库水的渗漏路径长度平均为2b+T;则上下游总的水力坡度为:

J=H/(2b+T)

据式(10-3),整个坝基的渗漏量为:

式中:B为坝轴线方向整个渗漏带宽度,m。

2.双层透水坝基

当坝基为两层透水层,其上层粉土、下层为砂砾石层时,若上层和下层的厚度分别为T1和T2(图10-6),则按式(10-5)计算单宽剖面渗漏量[6]:

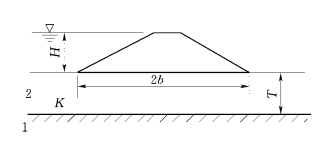
pagenumber_ebook=220,pagenumber_book=206

图10-5　单层透水坝基(摘自郭见扬等,1995)

1—隔水层;2—透水层;

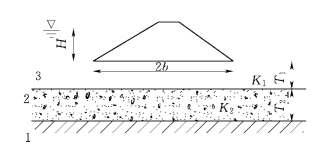
pagenumber_ebook=220,pagenumber_book=206

图10-6　双层透水坝基(摘自郭见扬等,1995)

1—隔水层;2—强透水层;3—弱透水层

pagenumber_ebook=220,pagenumber_book=206

若上层为砂砾石层,下层为黏性土(或粉土)层,因黏性土透水性较小,则可近似按式(10-3)计算,计算时把黏性土层当作隔水层处理[6]。

3.多层透水坝基

当坝基为多层土(水平产状),其渗透系数均不一样,但差值不太__大(在10倍左右)时,仍可按式(10-3)计算,此时,渗透系数用平均渗透系数K。K按加权法求得[6]:

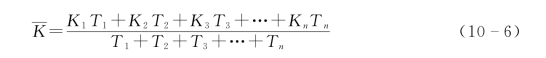
pagenumber_ebook=220,pagenumber_book=206

10.1.4.2 绕坝渗漏量Q绕坝的估算

绕坝渗漏水流有潜水类型和承压水类型两种,计算方法稍有不同。

1.潜水型时绕坝渗漏量的估算

(1)剖面计算法。首先在坝肩岩土体内绘制流线(在各向同性介质中,流线垂直于等水位线),对于均质的土体可按圆滑线处理(图10-7),然后在等水位线按单位宽度划分出剖面,如图10-7取1-1、2-2、3-3、4-4等。先计算出每个单宽剖面的渗漏量qi,最后将它们加起来,即得整个坝肩岩土体的渗漏量[6]。

即

各个单宽剖面的渗漏量可按达西公式求得[6]:

式中:Hi为第i剖面坝的上、下游水位差,m;Li为第i剖面的长度,即渗径长度,m;hi1、hi2分别为第i剖面上、下游透水层的厚度,m。

显然,每个剖面的渗漏量均有差别,离坝肩越远、剖面越长(即渗径越长),则渗漏量会越小,到一定距离后的剖面渗漏量就可以忽略了,这就是坝肩岩土体的渗漏范围。

当坝肩上、下游山坡有透水性弱的坡积层覆盖时(图10-8),由于该弱透水层起到铺盖作用,将减少库的渗漏量。此时,其单宽剖面渗漏量计算公式为[6]:

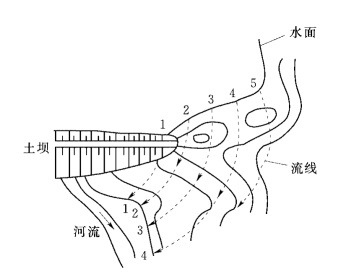
pagenumber_ebook=221,pagenumber_book=207

图10-7　沿山体基岩裂隙绕坝渗漏示意图(摘自郭见扬等,1995)

pagenumber_ebook=221,pagenumber_book=207

图10-8　边岸有坡积层时,沿流线绕坝渗流剖面图(摘自郭见扬等,1995)

pagenumber_ebook=221,pagenumber_book=207

式中:H1为上游水深,m;H2为下游水深,m;l1为坝肩上游坡积层的渗流长度,m;K1为坝肩上游坡积层的渗透系数,m/d;l2为坝肩主体岩层的渗流长度;m,K2为坝肩主体岩层的渗透系数,m/d;l3为坝肩下游坡积层的渗流长度,m;K3为坝肩下游坡积层的渗透系数,m/d。

(2)一次计算法。当边界条件较简单,绕坝渗漏流线接近圆形时(图10-9),绕坝渗漏量可用下式计算[6,16]:

式中:Q绕坝为绕坝渗漏量,m3/d;B为库岸可能漏水段的长度(从坝轴线算起),m;r0为坝肩与岩石接触面处绕坝渗漏流线圆轨迹半径,m;K为坝肩主体岩层的渗透系数,m/d;h1、h2分别为坝上、下游水头,m;H为大坝上下游水位差,m。

实际工作中,B的长度值需由d点来确定。如图10-9所示,B值相当于dc段的长度与r0之和。而c为坝端点,d点为地下潜水面与水库正常高水位面的交点,可根据勘探资料确定。

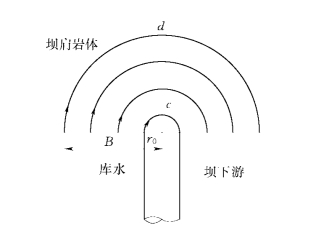
pagenumber_ebook=222,pagenumber_book=208

图10-9　流线近圆形的绕坝渗漏(摘自郭见扬等,1995)

(3)粗略计算法。当勘探资料缺乏时,不能确定绕坝渗流宽度B时,可按式(10-11)估算[6]:

式(10-11)是由式(10-10)令

0.366lg≈1.0而得的,作为粗略估算用,计算所得Q绕坝一般偏大。

2.承压水型时绕坝渗漏量的估算

将式(10-8)、式(10-10)、式(10-11)中的改为承压含水层的厚度T,则可得在承压水条件下各个计算绕坝渗漏量的公式,即[6]

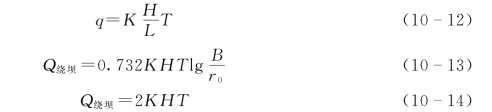
pagenumber_ebook=222,pagenumber_book=208

式中:T为承压含水层的厚度,m;其他变量意义同前。

10.1.4.3 库区渗漏损失量Q库区渗漏的估算

库水的渗漏损失是通过分水岭实现的。其渗漏量也可按达西公式计算。

1.单层岩土体分水岭隔水层水平时

假设前提条件:分水岭由单层岩土体组成,透水性较均一,隔水层埋藏不深。

无坡积层[图10-10(a)]时[6,17]:

pagenumber_ebook=222,pagenumber_book=208

式中:q为分水岭单宽剖面的渗漏量,m3/(d·m);K为分水岭岩土的渗透系数,m/d;H1为水库水位,m;H2为邻谷水位,m;L为库水在分水岭岩石内渗透的平均路径长,m;B为分水岭漏水段的宽度,m。

有坡积层[图10-10(b)]时[6]:

其中　 pagenumber_ebook=222,pagenumber_book=208

则

式中:l′、l″分别为分水岭水库一侧和邻谷一侧坡积层过水部分的厚度,m;l为除坡积层外,库水在分水岭岩石内渗透的路径长,m;K′、K″分别为分水岭水库一侧和邻谷一侧坡积层的渗透系数,m/d。

pagenumber_ebook=223,pagenumber_book=209

图10-10　单层岩土体分水岭渗漏量计算剖面(摘自　郭见扬等,1995)

(a)无坡积层;(b)有坡积层

2.单层透水层分水岭、隔水层倾斜时(图10-11)

如隔水层向水库倾斜,则有[6]:

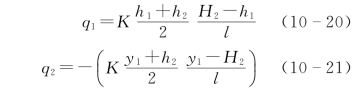
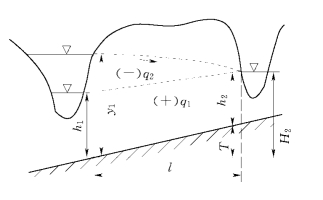
pagenumber_ebook=223,pagenumber_book=209

图10-11　单层透水层,隔水层倾斜剖面(据　郭见扬,1995)

单位库岸长度的渗漏损失为[6]:

qn=q1-q2

而H2=h2+T,T=il(i为隔水层的倾斜率),所以:

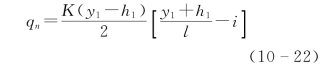
pagenumber_ebook=223,pagenumber_book=209

式中:qn为单位库岸长度的渗漏损失,m2/d;K为分水岭岩石层的渗透系数,m/d;H2为邻谷水头值,m。

如渗漏段的长度为B(m),则库区的总渗漏量为[6,17]:

3.双层透水层分水岭时

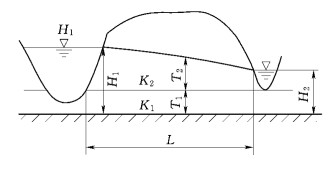
pagenumber_ebook=223,pagenumber_book=209

图10-12　双层透水层剖面(据　郭见扬,1995)

如图10-12所示,根据达西公式得[6]:

pagenumber_ebook=223,pagenumber_book=209

其中

则

式中:T1为下层透水层的厚度,m;T2为上层透水层过水部分的平均厚度,m;其余符号意义同前。

10.1.4.4 渗透系数K的确定

可根据坝址岩体的压水实验资料,由式(5-9)估算。但值得注意的是,由于基岩的透水性极不均一,透水的结构面多为高角度的裂隙,而压水试验孔都为铅直孔;另外勘探时揭露这些裂隙的机会不多,偶有揭露,也常会大量漏水,抬不起水头,无法取得这些大裂隙发育段的压入流量Q值。但决定岩体透水性的,恰恰正是这些较大的裂隙。这样,由于较完整岩石试段的透水性不能代表地段的透水性,故换算出的K值一般均偏小。而且透水性越弱,K值偏小越多[16]。

因此,根据岩石的压入流量Q值计算K时,不能简单地采用式(5-9),而应当根据当地的具体情况,最好在每一个工地上选择几个钻孔作比较试验,通过抽、压水对比,作出K=f(q)关系曲线,或求出不同地段不同岩层的经验K(或q)值,而在该地应用,这比直接用式(5-9)为好。但到目前为止,K与q值的换算关系还存在不少问题,需要进一步研究[16]。

10.1.4.5 岩溶地区水库总渗漏量Q的计算

在喀斯特发育强烈区的水库,由于岩溶管道水的运动已不再是达西流,此时如再利用地下水动力学的有关公式进行计算就不太合适。因此GB 50287—1999《水利水电工程地质勘察规范》附录B.0.5条的规定,岩溶地区的水库,其渗漏量必须采用地下水动力学法和水量均衡法进行计算,并相互验证。

水量平衡法是根据多年实测的水库水位、水面蒸发量、农业灌溉用水量等资料,利用水位—库容的关系资料,来计算水库的年蓄变量、年平均库容量、年实际库面蒸发量。

依据水量均衡原理,水库的渗漏量为[18]:

式中:Q为水库总的渗漏量;WQ为上游来水量;WP为水库水面直接接受降水补给量;WE为水库水面蒸发量;WF为水库放水量;W蓄为水库蓄变量。

以云南省昭通市渔洞水库为例。它位于金沙江二级支流居乐河上,水库的控制径流面积约为709km2。经分析发现,水库存在岩溶型渗漏。该水库的径流面积共计709km2,采用水库上游跳石站观测资料还原计算跳石至水库区间的入流量;蒸发量采用渔洞站E601的观测资料,出流量采用水库实测出流观测资料。计算时段选用1999年3月(该时段内基本无降水,计算的结果相对较准确)。计算得:月入流量WQ为474.8万m3,蒸发量WE为113.2万m3,出流量WF为4468.5万m3,再根据该月库容的变化量W蓄,最终求得水库的总渗漏量Q为1.0万m3[18]。

水文地质勘察：准确估算水库渗漏量

相关推荐