水文地质勘察：逐点求参法的应用

2023-09-18 理论教育版权反馈

【摘要】：5.7.3.1 逐点求参法对于一维稳定流场瞬时注入示踪剂的二维弥散试验,其弥散系数可按下两式求得[10]:式中:u为地下水的实际流速,m/h;C1为t1时刻减去背景值后的示踪剂的浓度,g/L;C2为t2时刻减去背景值后的示踪剂的浓度,g/L。

目前,确定二维地下水动力弥散参数的方法有直线图解法、逐点求参法、标准曲线配线法等等。限于篇幅,在此只介绍前2种。

5.7.3.1 逐点求参法

对于一维稳定流场瞬时注入示踪剂的二维弥散试验,其弥散系数可按下两式求得[10]:

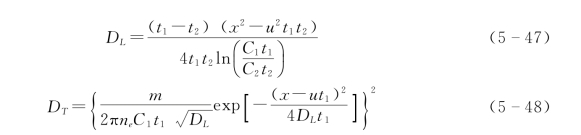
pagenumber_ebook=130,pagenumber_book=116

式中:u为地下水的实际流速,m/h;C1为t1时刻减去背景值后的示踪剂的浓度,g/L;C2为t2时刻减去背景值后的示踪剂的浓度,g/L。

资料整理时,利用2个时刻t1、t2及其所对应的浓度C1、C2的值,先按式(5-47)求得DL,然后再用式(5-48)求得DT。

5.7.3.2 直线图解法

在图5-34中,当监测孔位于x轴上,其坐标为(x0,0),把x=x0及y=0代入式(5-46)中,则式(5-46)就简化为下式[11]:

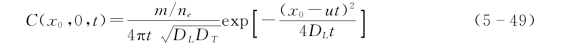
pagenumber_ebook=130,pagenumber_book=116

为了利用(x0,0)监测孔上的监测数据来反求式(5-49)中的参数,郭建青等人(2011)推导出以下线性方程[11]:

其中　

pagenumber_ebook=130,pagenumber_book=116

式(5-53)及式(5-54)中,

pagenumber_ebook=130,pagenumber_book=116

可利用作图法来求解式(5-50)。因为在以Y0为纵坐标轴、X0为横坐标轴的体系中,式(5-50)是一条直线。考察式(5-53)、式(5-54)可发现,Y0i和X0i均为试验中观测的数据函数,而常数项A0和B0则含有欲求的纵向弥散系数DL和地下水流速u。只要通过作图求得方程式(5-50)后,即可由式(5-58)和式(5-59)算出DL和地下水流速u的值。即[11]:

由式(5-51)得　

由式(5-52)得　

仅利用(x0,0)监测孔上的监测数据还不能求得横向弥散系数DT,需用不在x轴上的监测孔的监测数据才能求出。假设监测孔的位置为(x1,y1),把x=x1,y=y1代入式(5-46)得[11]:

pagenumber_ebook=131,pagenumber_book=117

为了利用(x1,y1)监测孔上的监测数据来反求式(5-60)中的参数,郭建青等人(2011)又推导出以下线性方程[11]:

其中　

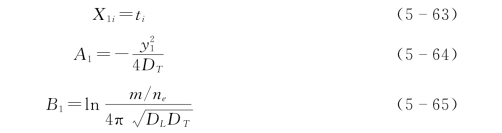
pagenumber_ebook=131,pagenumber_book=117

显然,可由式(5-64)求得DT,即:

还可由式(5-65)求得有效孔隙率,即:

直线图解法求参的思路是:先用位于x轴的观测孔来求出纵向弥散系数DL和地下水流速u,再利用不位于x轴上的观测孔的观测数据来求出横向弥散系数DT和有效孔隙率ne。具体步骤详见下述算例的求解过程。

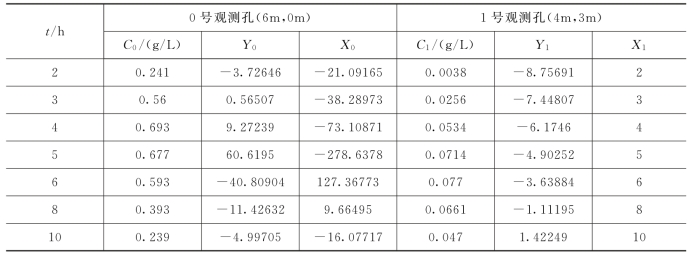
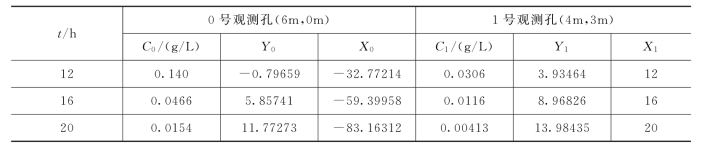
【例题5.4】某场地弥散试验中,含水层厚度10m,投放试剂20kg,表5-14中列出了0号孔与1号孔中示踪剂的浓度随时间的变化过程。现采用直线图解法求出纵向弥散系数DL、横向弥散系数DT、地下水实际流速u及有效孔隙率ne。

表5-14　观测孔的观测数据及计算中间数据(摘自郭建青,2011)

pagenumber_ebook=131,pagenumber_book=117

续表

pagenumber_ebook=132,pagenumber_book=118

解:先用0号孔观测数据求参:

(1)用式(5-55)～式(5-57)分别求得G0=0.1871,H0=8.60和F0=0.43614。

(2)用式(5-53)、式(5-54)计算对应于不同观测时间ti的Y0i、X0i,结果列于表5-14中。

(3)利用一元线性回归法计算直线方程式(5-50)中的常数A0=-9.00,B0=-0.24984。具体算法可参考本书的附录3。

(4)利用式(5-58)、式(5-59)分别求得纵向弥散系数DL=1.00m2/h,地下水流速u=1.00m/h。再用1号孔的观测数据继续求参。

(5)利用式(5-62)计算对应于ti的Y1i,并令X1i=ti。结果列于表5-14中。(6)利用一元线性回归法求得直线方程式(5-61)中的常数A1=-11.22738和B1=1.26222。

(7)因m=20/10=2.0kg/m,利用式(5-66)、式(5-67)分别算出横向弥散系数DT=0.200m2/h,有效孔隙率ne=0.101。

【讨论】从[例题5.4]计算结果可发现,利用弥散试验反求所得的地下水平均流速u与直接利用式(5-39)来计算的结果并不一致。若用示踪剂浓度的峰值在0号孔出现的时间(即4h)来计算地下水平均流速u,由式(5-39)得:

此结果为何与上述算例的结果不同?这主要因为受实际含水介质非均值各向异性的影响所致。本例0号观测孔测定得到的示踪剂浓度-时间关系曲线并不对称(峰值前4小时,而峰值后超过16小时,曲线两翼严重不对称),所求得的平均流速(u=1.00m/h)其实代表了能到达0号孔的所有示踪剂微粒的平均速度值。可见,利用弥散试验所求得的地下水平均流速值更为精确。而式(5-39)只有在观测孔中的示踪剂浓度-时间关系曲线呈正态分布曲线时才能得到准确的结果。

由此可见,通过野外弥散试验不仅能求出比较准确的、能反映真实情况的水动力弥散系数DL及DT,还能求得较为准确的地下水流速u及有效孔隙率ne,这是其他水文地质试验无法比拟的优点。不过由于式(5-45)并未考虑示踪剂被含水介质吸附,而是假定所投放的示踪剂全部能在含水层中迁移和弥散,因此,用于计算效孔隙率的m值偏大[见式(5-67)],引起所求得的ne值偏大。示踪剂被含水介质吸附量越多,ne值偏大越严重。

水文地质勘察：逐点求参法的应用

相关推荐