三铰拱为静定结构,其全部支座反力和内力都可由平衡条件确定。图12-22竖向荷载作用下的三铰拱内力计算1.支座反力的计算三铰拱有四个支座反力。即拱的竖向反力与相应简支梁的竖向反力相同。试计算图12-23所示三铰拱的内力,并绘制其内力图。图12-24三铰拱内力图弯矩图;剪力图;轴力图......
2025-09-29
框架结构承受的水平荷载主要是风荷载和水平地震作用。为简化计算,可将风荷载和地震作用简化成作用在框架节点上的水平集中力。在水平荷载作用下,框架将产生侧移和转角,框架的变形图和弯矩图如图4-15所示。
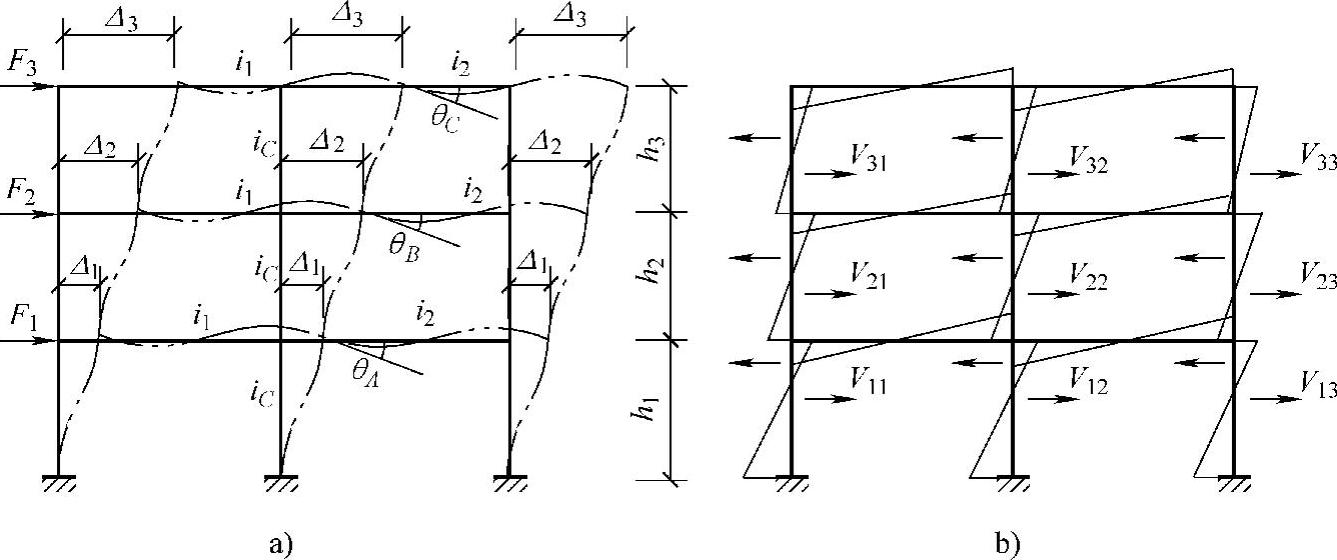
图4-15 水平荷载作用下框架变形和弯矩示意图
由图4-15a可知,底层框架柱下端无侧移和转角,上部各节点有侧移和转角。由图4-15b可知,规则框架在水平荷载作用下,在柱中弯矩均为直线,均有一零弯矩点,称为反弯点,若求得各柱反弯点位置和剪力,则柱的弯矩就可求。水平荷载作用下框架结构的内力和侧移可用结构力学方法计算,常用的近似算法有迭代法、反弯点法、D值法和门架法等。本节主要介绍反弯点法和D值法的基本原理和计算要点。
1.反弯点法
(1)反弯点法的计算假定 对层数不多的框架,柱轴力较小,截面面积也较小,梁的截面面积相对较大,框架梁的线刚度要比柱的线刚度大得多,框架节点的转角很小。当框架梁、柱线刚度比大于3时,框架在水平荷载作用下梁的弯曲变形很小,可以将梁的刚度视为无穷大,框架节点转角为零,其变形可简化为图4-16。
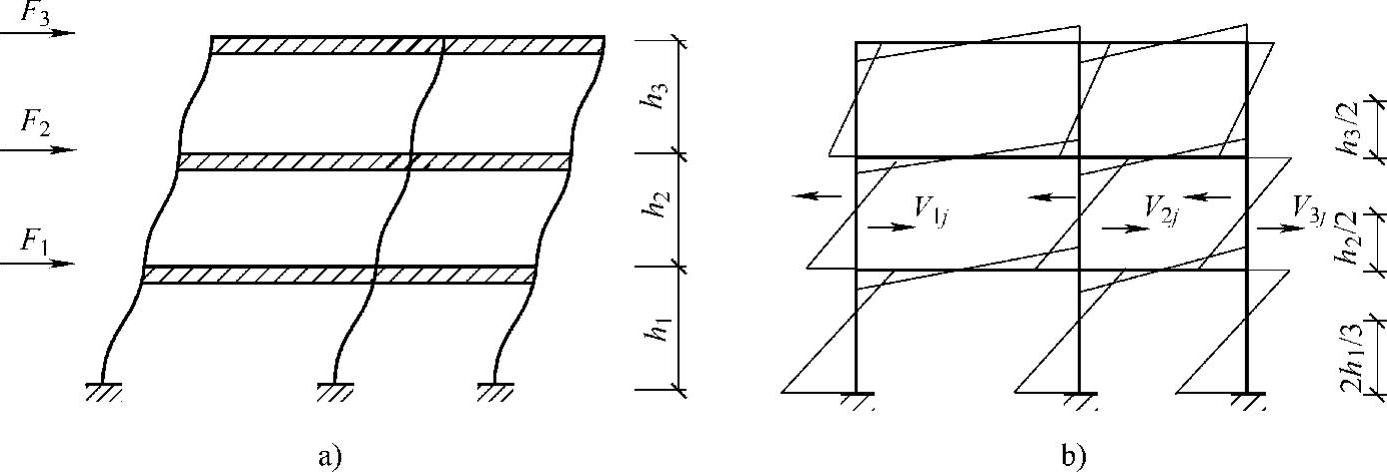
图4-16 反弯点法示意图
计算假定:①不考虑节点转角,即转角为0;②不考虑横梁轴向变形,即假定梁刚度为无穷大。
反弯点法的主要工作有两个:①求出各柱反弯点处的剪力;②确定反弯点高度。
(2)柱反弯点位置的确定 当梁的线刚度假定为无穷大,且柱端无转角时,柱两端弯矩相等,反弯点在柱的中点。对于上层各框架柱,当框架梁柱线刚度比大于3时,柱端转角很小,反弯点接近中点,一般假定就在柱的中点,即反弯点高度y=h/2。对于底层柱,由于底端固定而上部有转角,反弯点向上移,通常假定反弯点在距底端2/3高度处,即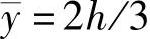 。
。
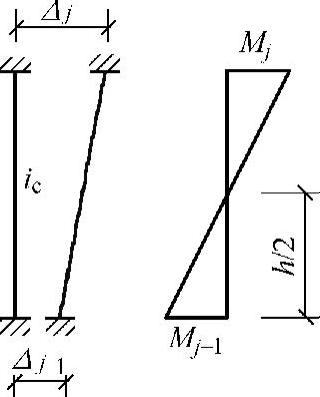
图4-17 两端固接柱侧移时变形和弯矩图
(3)柱剪力的确定
1)柱的侧移刚度d。根据前述假定,框架柱端无转角但有水平位移时(见图4-17),柱剪力与水平位移的关系为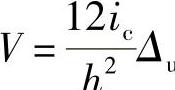 。
。
设 
则 
式中 ic——柱的线刚度;
h——柱高度;
Δu——柱端侧移,Δu=Δuj-Δuj-1;
d——柱的侧移刚度,其物理意义是柱上、下两端有单位侧移时,柱中产生的剪力。
2)柱剪力的确定。由计算假定可知,不考虑横梁变形时,同层各柱顶的相对位移均相等。由此可得第j层i根柱剪力:Vj1=dj1Δuj,Vji=djiΔuj。第j层柱的总剪力为Vj=Vj1+Vj2+…+Vji,Vj=(dj1+dj2+…+dji)Δuj。
第j层的侧移为 
则第j层第m柱剪力为 
可见各柱剪力的大小是按各柱侧移刚度分配给各柱的。
(4)梁端、柱端弯矩的计算 求出各柱剪力后,根据已知各柱反弯点位置,可求出各柱端弯矩。求出所有柱端弯矩后,根据节点力矩平衡求梁的弯矩。
1)柱端弯矩的计算。
柱上端弯矩 
柱下端弯矩 
2)梁端弯矩的计算。梁端总弯矩可由节点平衡求得。并按各梁的线刚度分配。
边节点Mlb=∑Mc (4-7)
中间节点 

【例4-3】框架计算简图如图4-18所示,用反弯点法求梁柱弯矩。
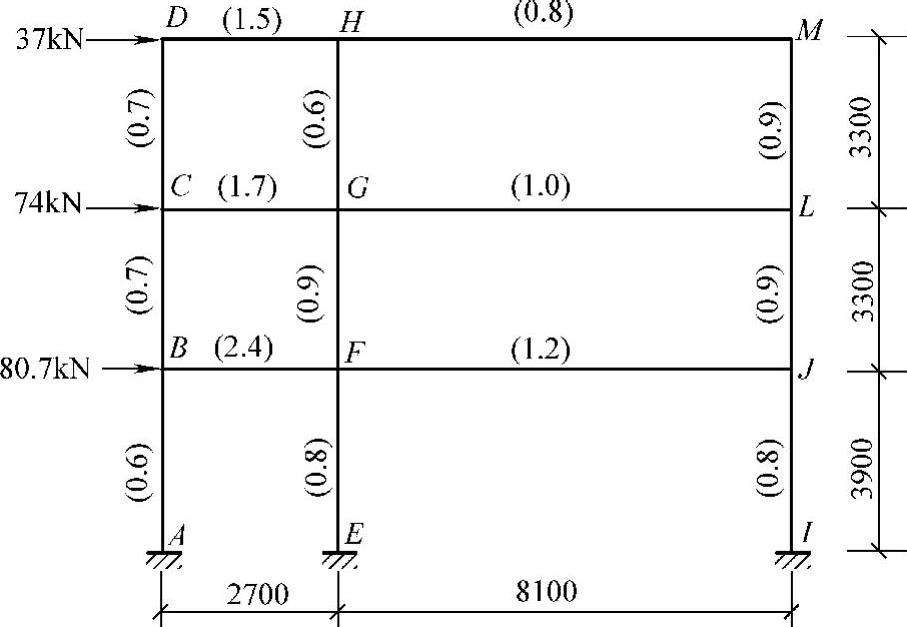
图4-18 框架计算简图
解:(1)求出各柱在反弯点处的剪力值
第三层 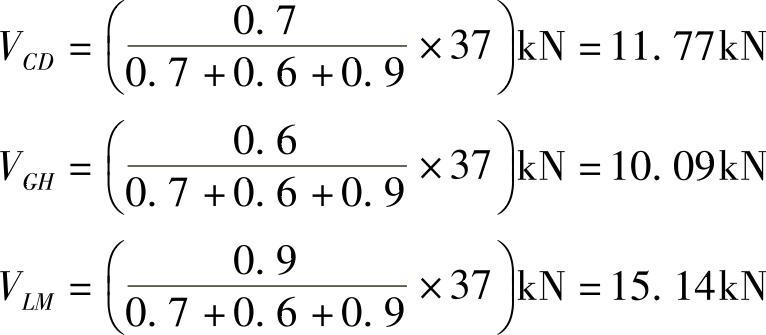
第二层 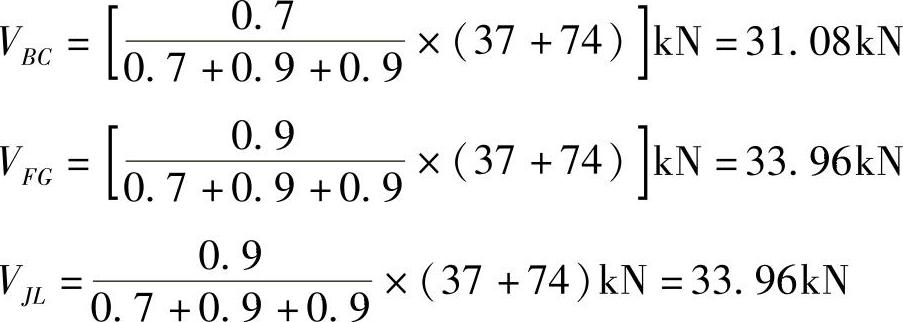
第一层 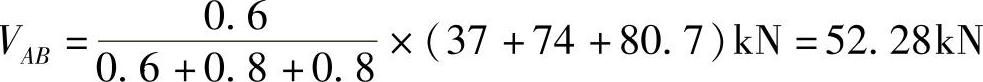
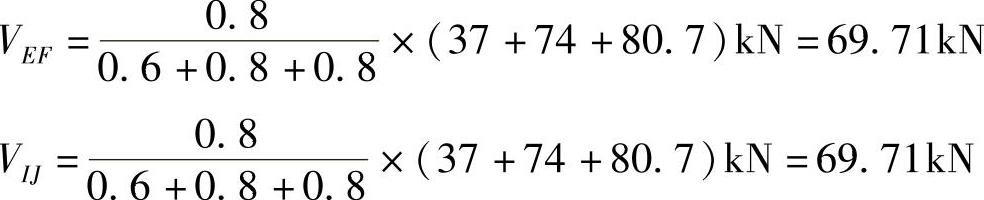
(2)求出各柱柱端的弯矩
第三层 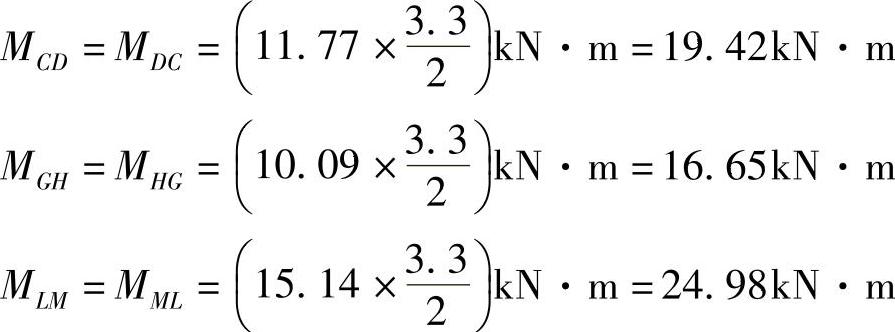
第二层 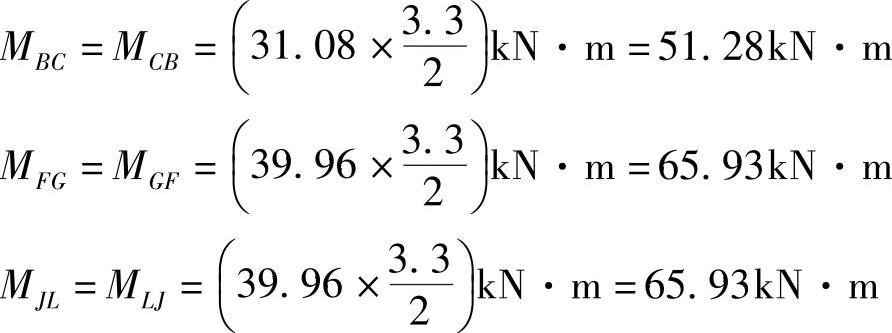
第一层 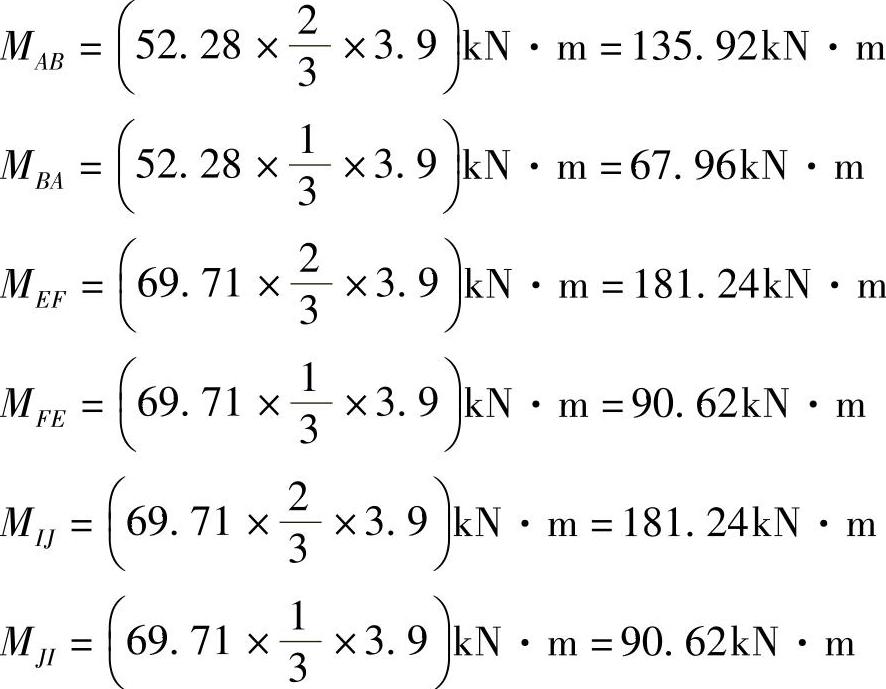
(3)求出各横梁梁端的弯矩
第三层 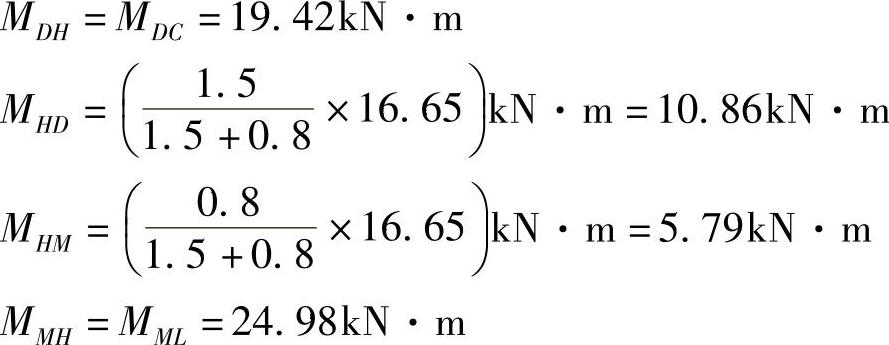
第二层 
第一层 
(4)绘制各杆的弯矩图 如图4-19所示。
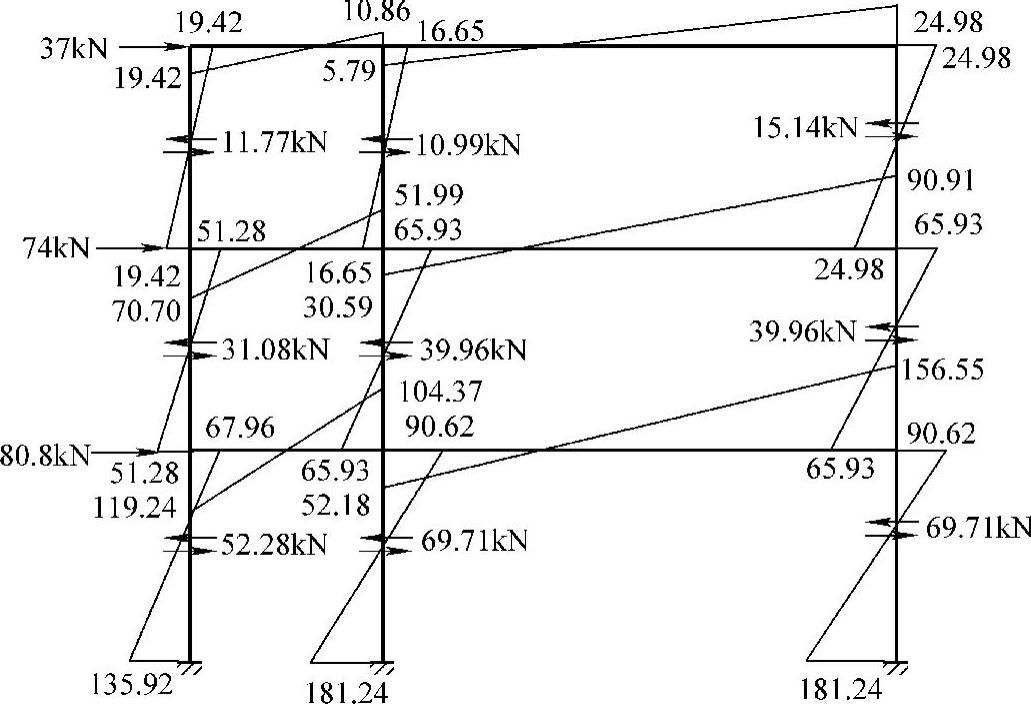
图4-19 例4-3弯矩图(单位:kN·m)
2.D值法
计算层数较多的框架时,由于柱截面尺寸较大,梁柱相对线刚度比会减少,框架节点的转角对柱抗侧刚度和反弯点位置会有较大的影响。用反弯点法计算时,会有较大的误差。此时可用D值法计算。D值法是在反弯点法的基础上,考虑上述的影响,对柱的抗侧刚度和反弯点位置予以修正,所以此法也称修正反弯点法。D值法计算要点如下:
(1)柱的侧移刚度D值 当柱两端有相对侧移Δu和转角θ时,柱的剪力为

设D=V/Δu,则

式中 D——修正后柱的抗侧刚度,与Δu、θ有关。
图4-20a所示多层框架,在水平荷载作用下,各节点将产生侧移和转角。框架节点A、B及与之相连的各杆件变形情况如图4-20b所示,为方便分析,推导D值时,作如下假定:①假定柱AB以及与柱AB相邻的各杆的杆端转角均为θ;②假定柱AB以及与其相邻的上、下层柱的线刚度均为ic;③假定各层层间侧移均为Δu。
汇交于节点A的各杆端弯矩为
MAE=(4i3+2i3)θ=6i3θ,MAG=6i4θ
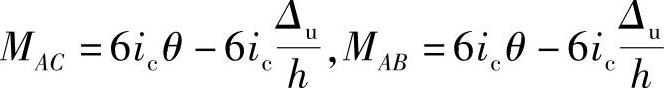
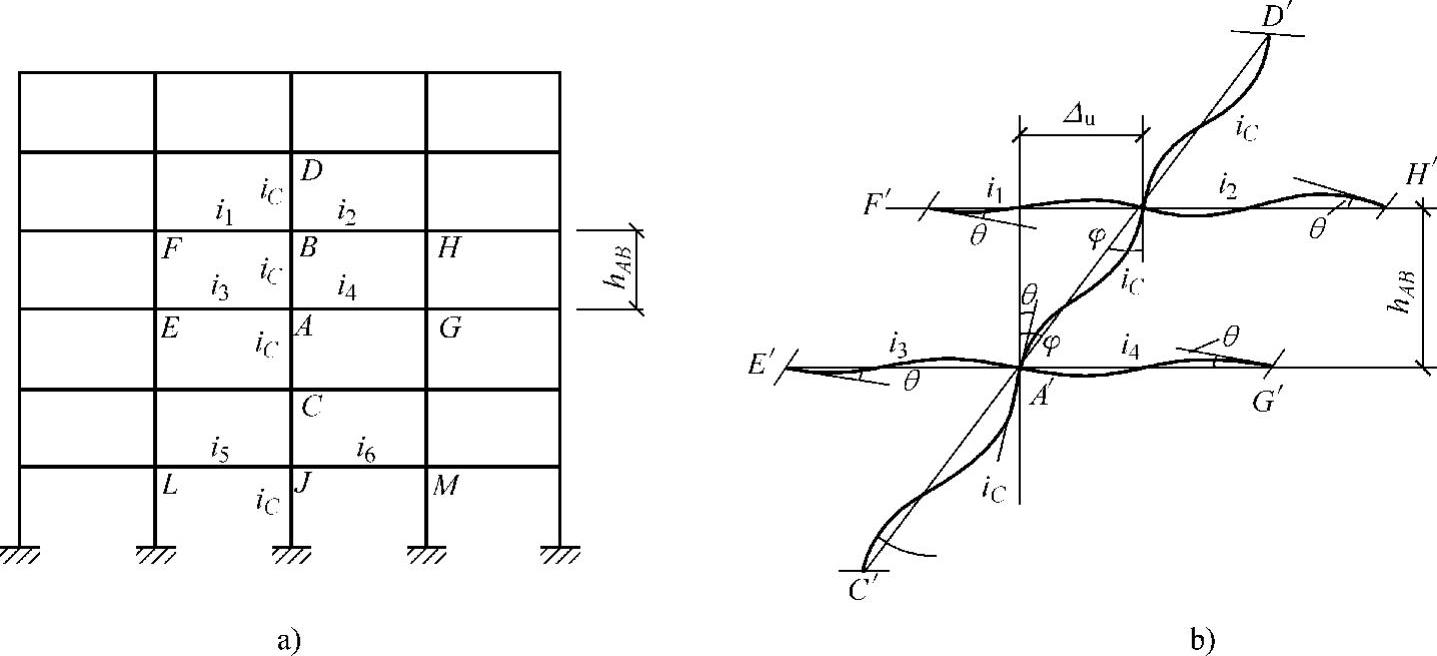
图4-20 框架侧移与节点转角
由节点A力矩平衡条件有 MAE+MAC+MAG+MAB=0
可得 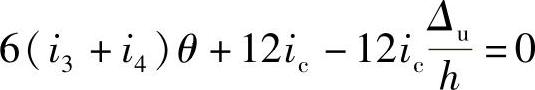
同理,由节点B力矩平衡得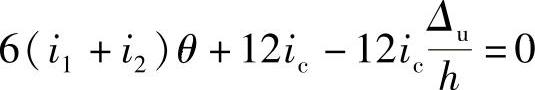
将上两式相加、整理得 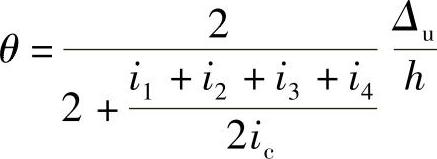
令 
则 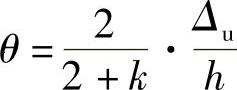
k为梁柱线刚度比。对于边柱i1=i3=0,可得

对于框架底层柱,由于底端为固定端,无转角,可按类似方法推导出梁柱线刚度比(https://www.chuimin.cn)

将θ代入式(4-11)得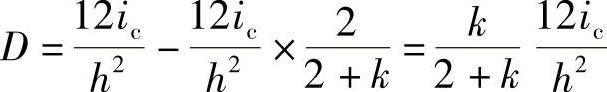
令 
则 
α表示梁柱线刚度比对柱刚度的影响,当梁柱线刚度比k值无穷大时,α=1,D=d。当梁柱线刚度比较小时,α<1,D<d。因此,α称为柱刚度修正系数,柱刚度修正系数见表4-3。
表4-3 柱刚度修正系数
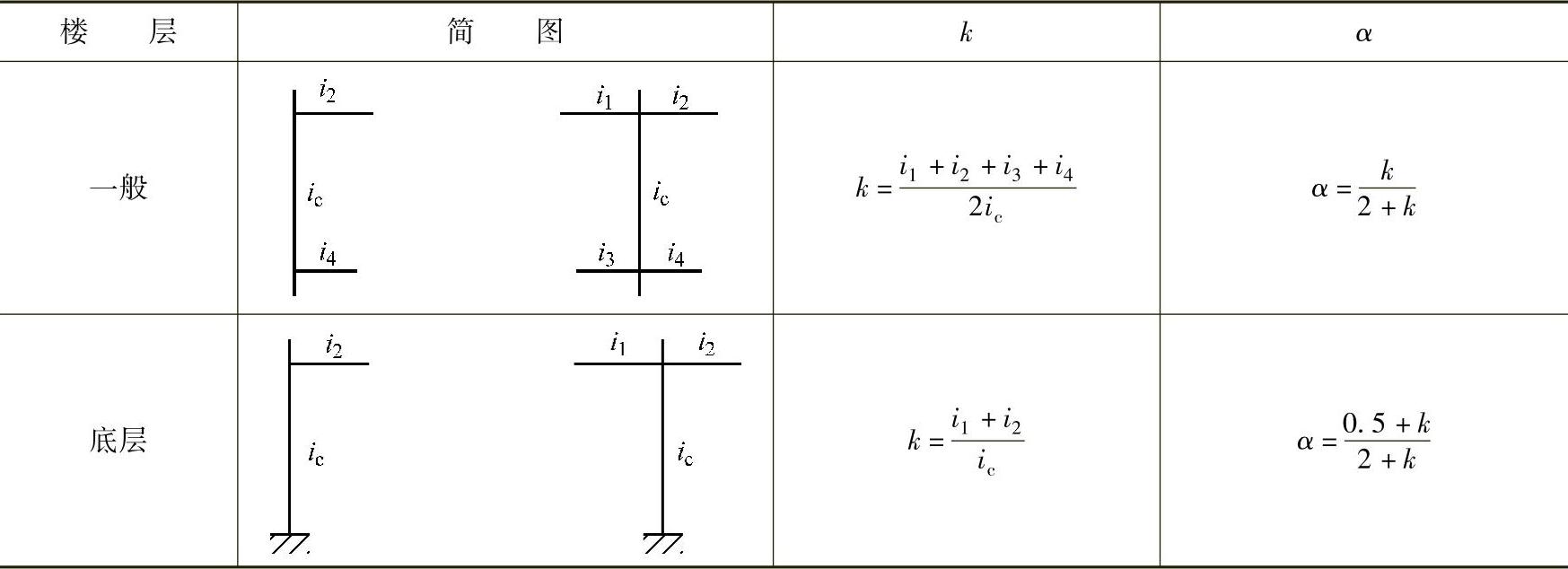
(2)柱反弯点位置 反弯点到柱下端的距离与柱高度的比值,称为反弯点高度比,用y表示。反弯点到柱底的距离即为yh。
柱反弯点的位置与柱两端的约束条件有关,当柱上、下两端固定或转角相同时,反弯点在中点;两端约束刚度不同时,转角也不相同,反弯点移向转角较大的一端,也就是向约束刚度较小的一端移动。影响柱两端约束刚度的主要因素有荷载的形式,结构总层数与该层所在位置,柱上、下层横梁刚度比,柱上、下层层高变化。
在D值法中,通过力学分析求得标准情况下的标准反弯点高度比y0,再根据上、下层横梁刚度比及上、下层层高变化,对y0进行修正。
1)标准反弯点高度比y0。标准反弯点高度比是在等高、等跨,各层梁柱线刚度都不变的多层框架在水平荷载作用下求得的反弯点高度比。表4-4、表4-5列出了在均布水平荷载、倒三角形分布荷载下的y0。
表4-4 均布水平荷载下各层柱标准高度比y0
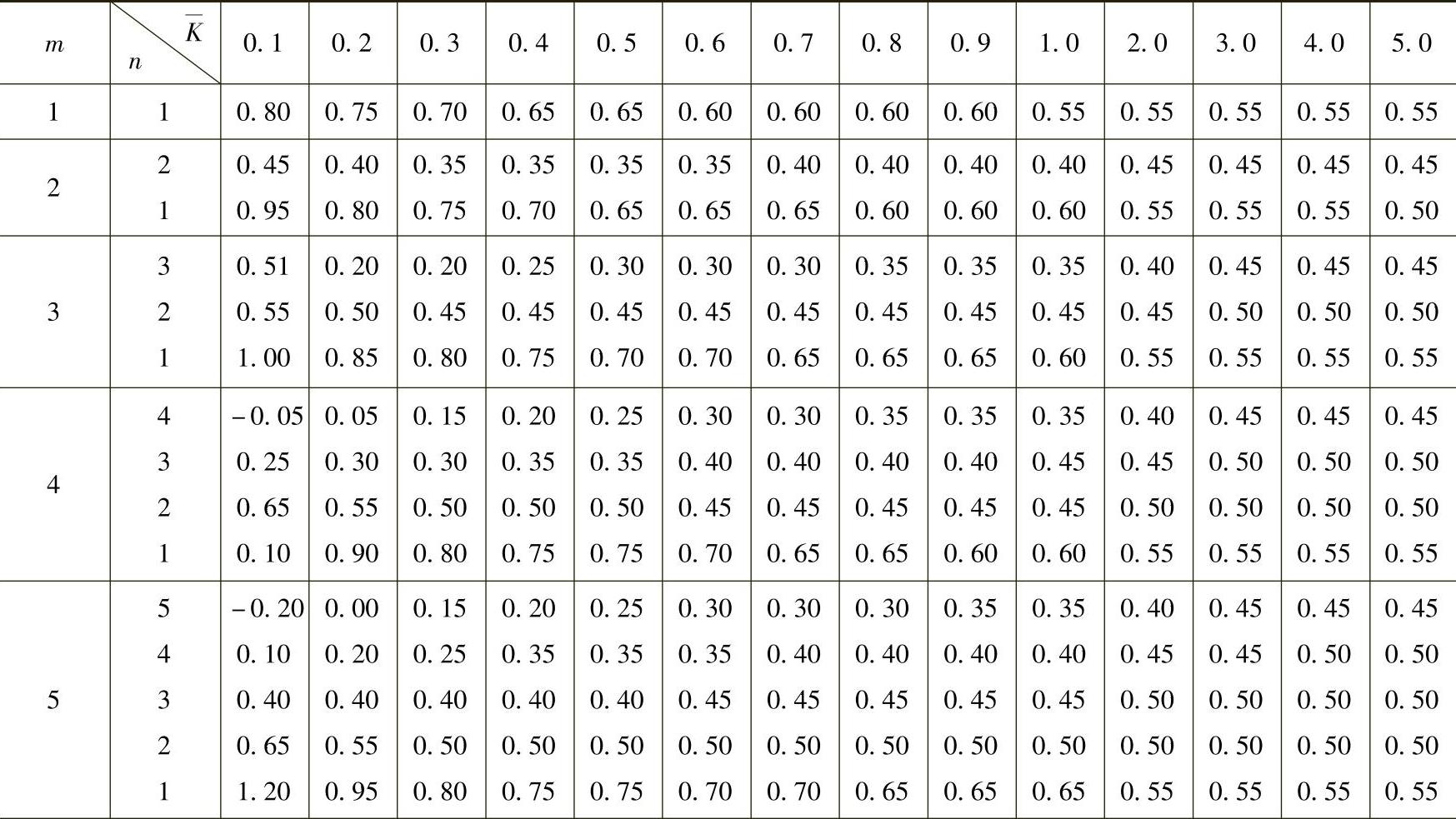
(续)
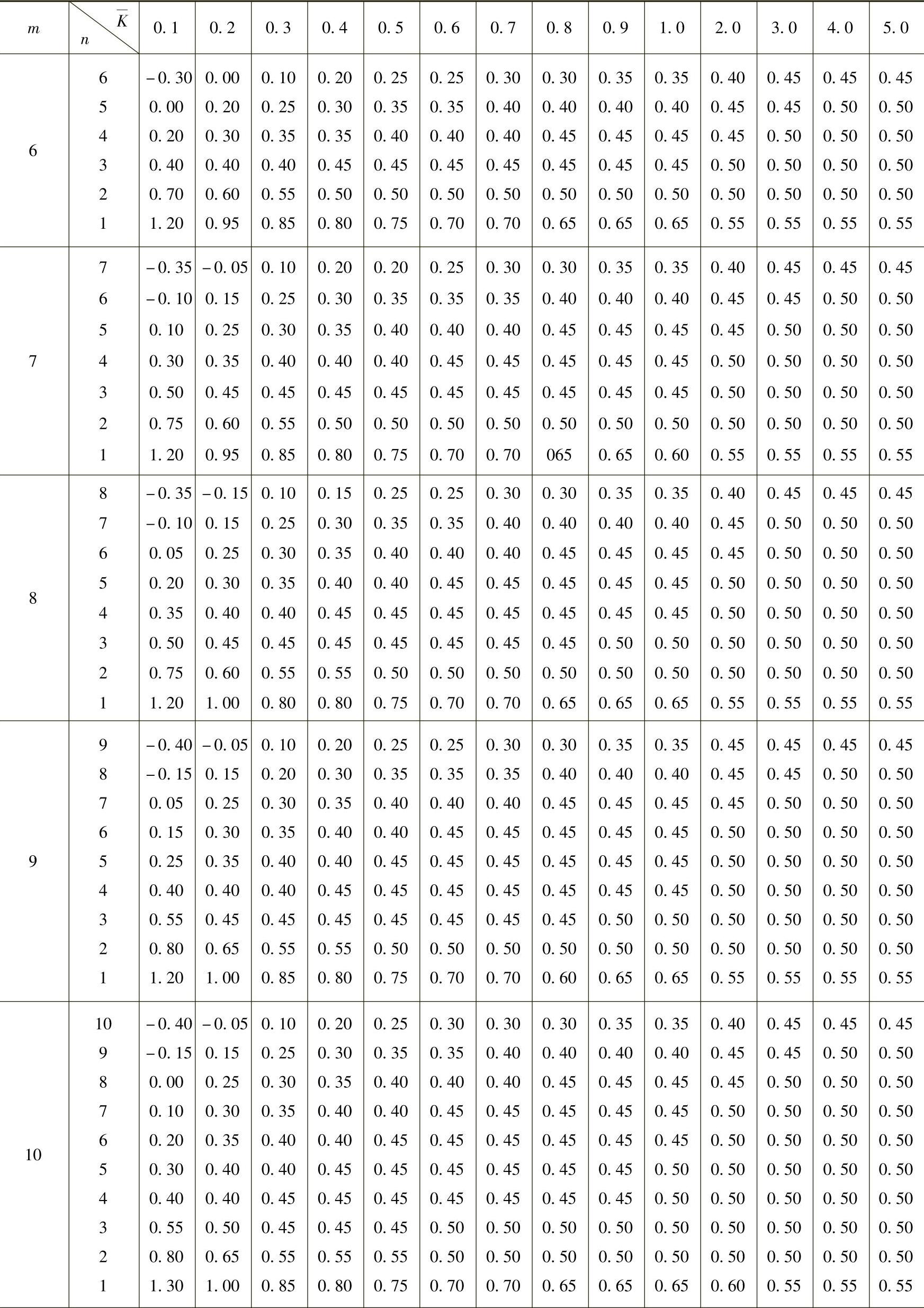
(续)
注: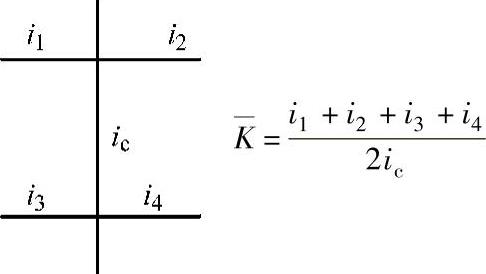
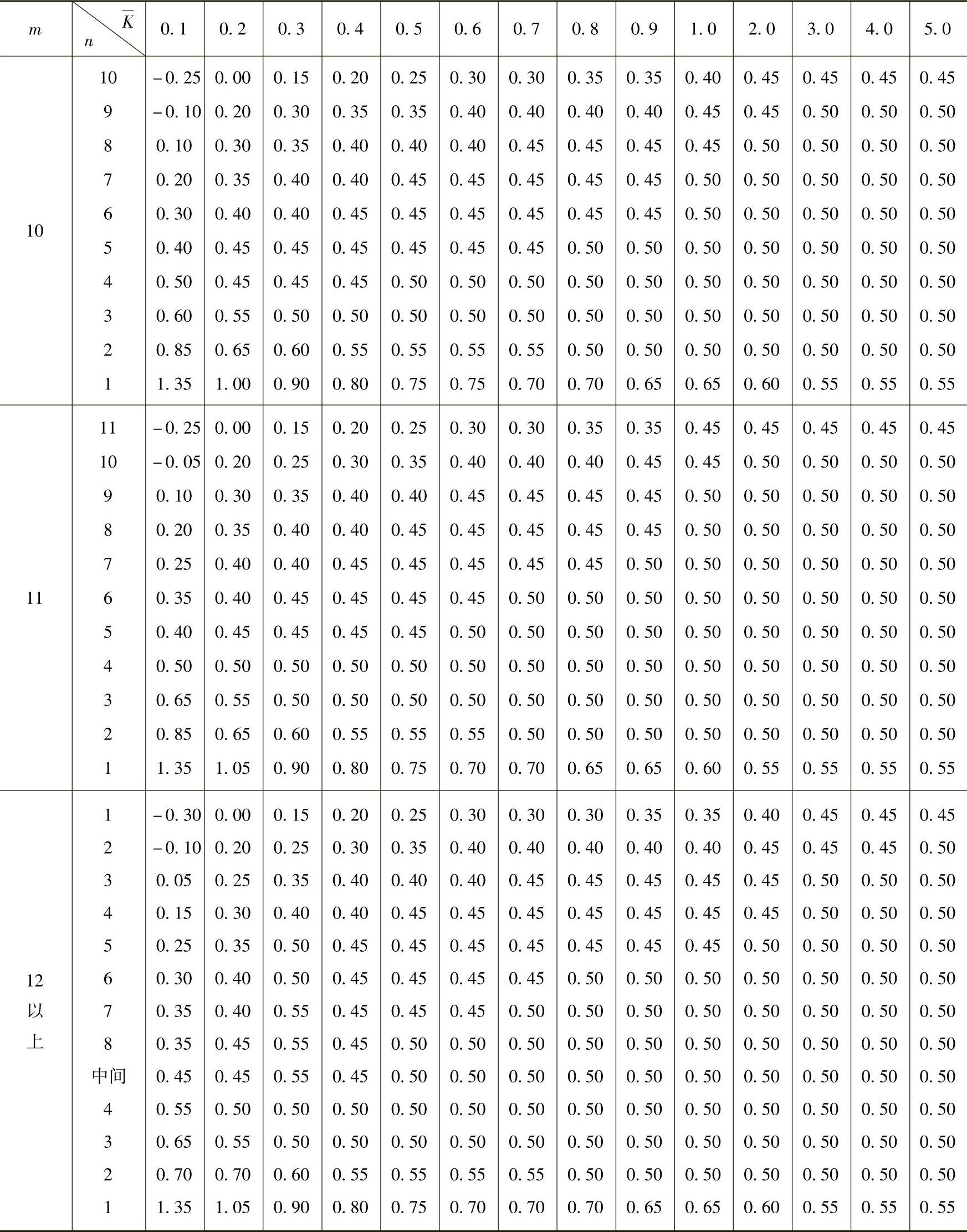
表4-5 倒三角形分布荷载下标准反弯点高度比y0
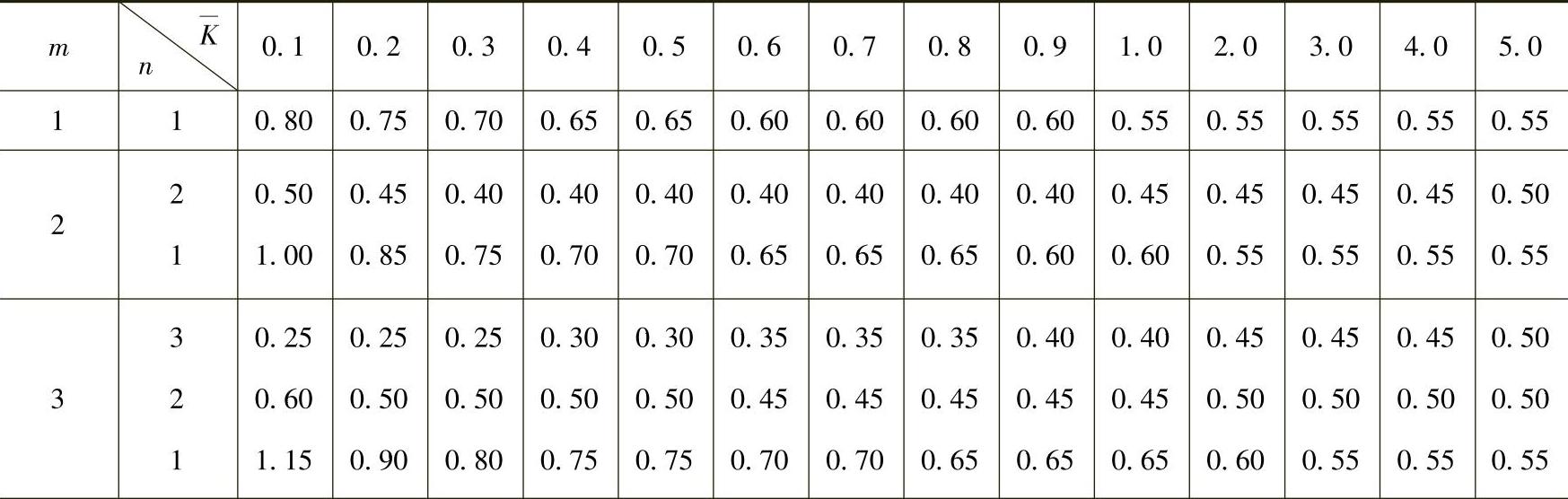
(续)
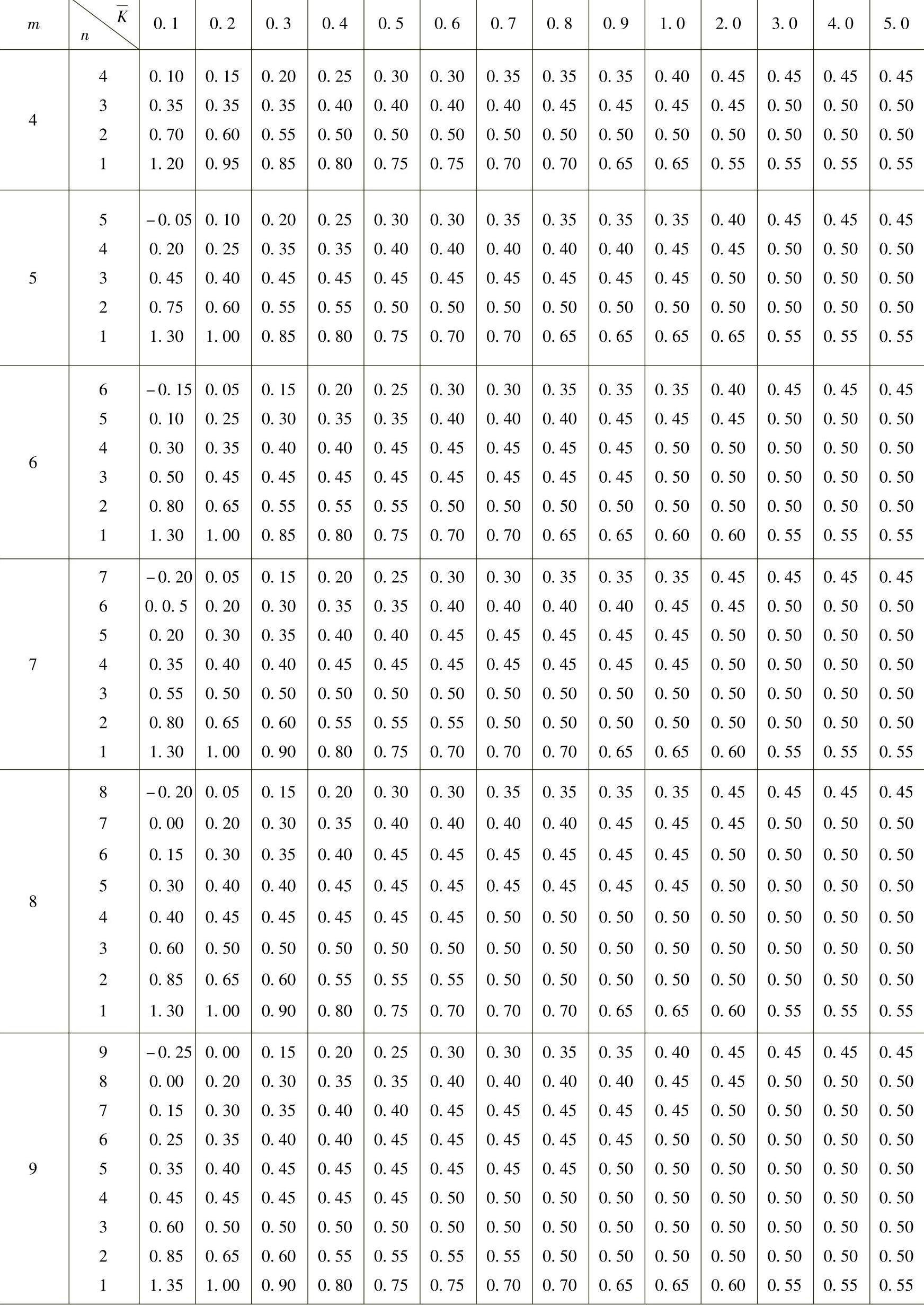
(续)
2)上、下层横梁刚度不同时的反弯点高度比位置修正值y1。当某柱的上、下层横梁刚度不同,柱上、下节点转角也不同时,反弯点位置有变化,应将标准反弯点高度比y0加以修正,修正系数为y1(见图4-21a及表4-6)。
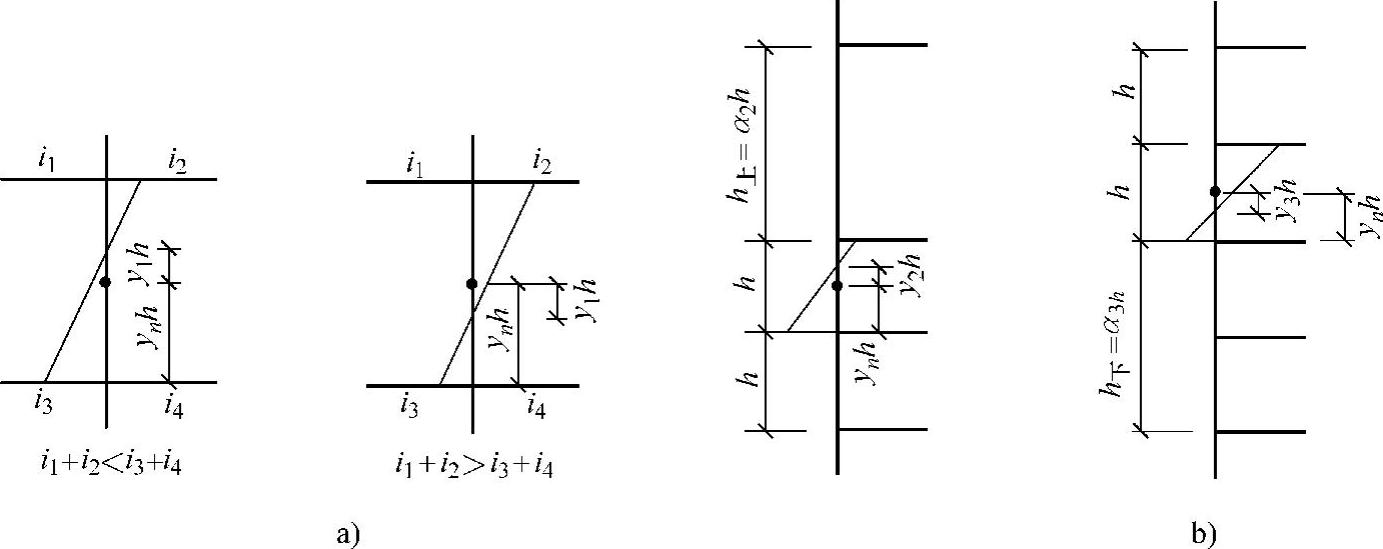
图4-21 反弯点位置变化图
a)上、下层梁刚度变化 b)层高变化
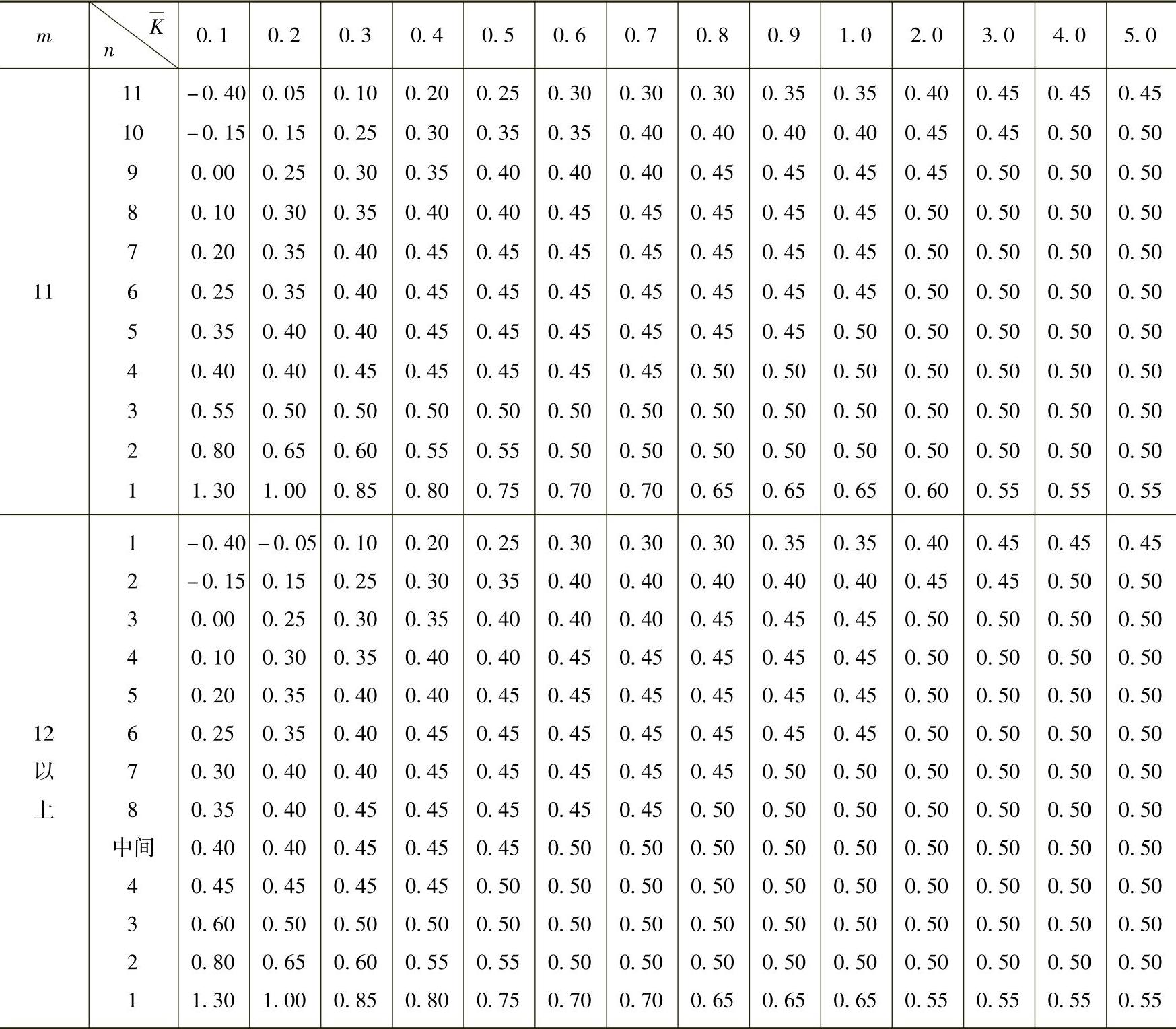
表4-6 上、下层横梁刚度变化时反弯点高度比的修正值y1
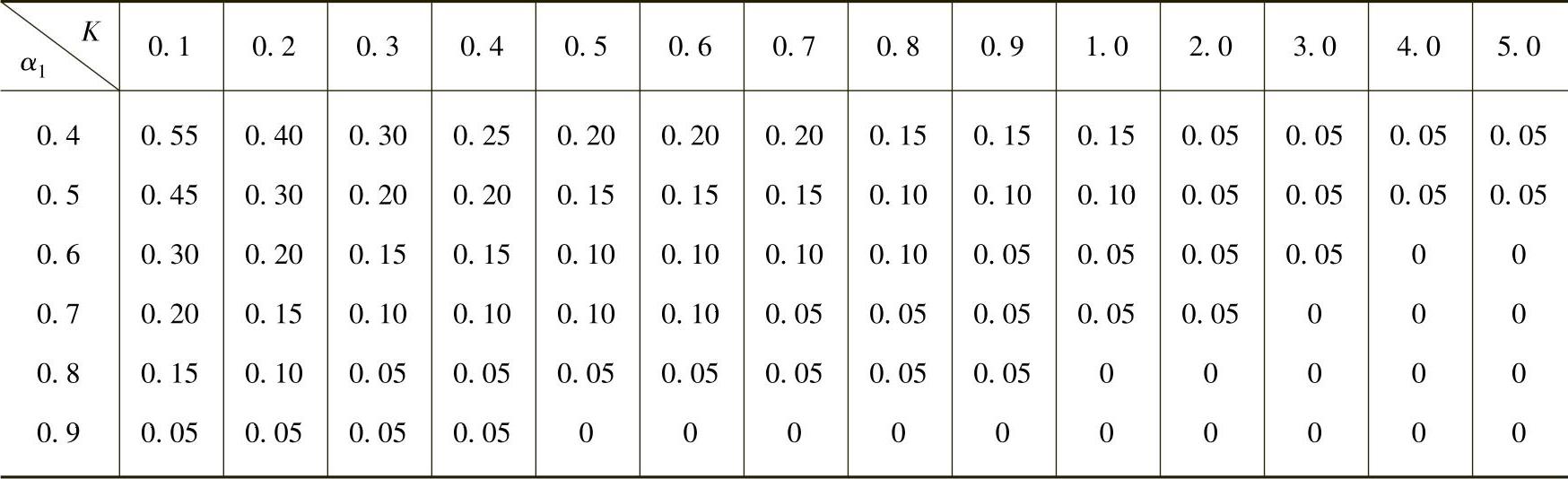
注: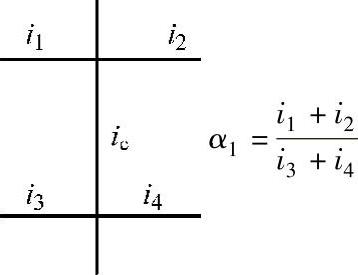 ,当i1+i2>i3+i4时,则α1取倒数,即
,当i1+i2>i3+i4时,则α1取倒数,即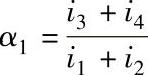 ,并且y1取负号;K按表4-3计算;底层可不考虑此项修正,即取y1=0。
,并且y1取负号;K按表4-3计算;底层可不考虑此项修正,即取y1=0。
当i1+i2<i3+i4时,反弯点应向上移动,取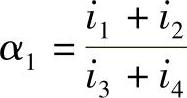 ,y1取正值;当i1+i2>i3+i4时,反弯点应向下移动,取
,y1取正值;当i1+i2>i3+i4时,反弯点应向下移动,取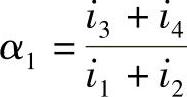 ,y1取负值;底层柱不考虑修正值y1。
,y1取负值;底层柱不考虑修正值y1。
3)上、下层层高变化时的反弯点高度比位置修正值y2和y3。层高有变化时,反弯点位置的变化如图4-21b所示。α2为上层层高h上和本层层高h之比。当α2>1时,反弯点向上移动,y2为正值;当α2<1时,反弯点向下移动,y2为负值;顶层不考虑修正值y2。α3为下层层高h下和本层层高h的比值。当α3>1时,反弯点向下移动,y3为负值;当α3<1时,反弯点向下移动,y3为正值;底层不考虑修正值y3。
柱反弯点高度比可用下式计算
y=y0+y1+y2+y3 (4-17)
上、下层层高度变化时修正值y2和y3见表4-7。
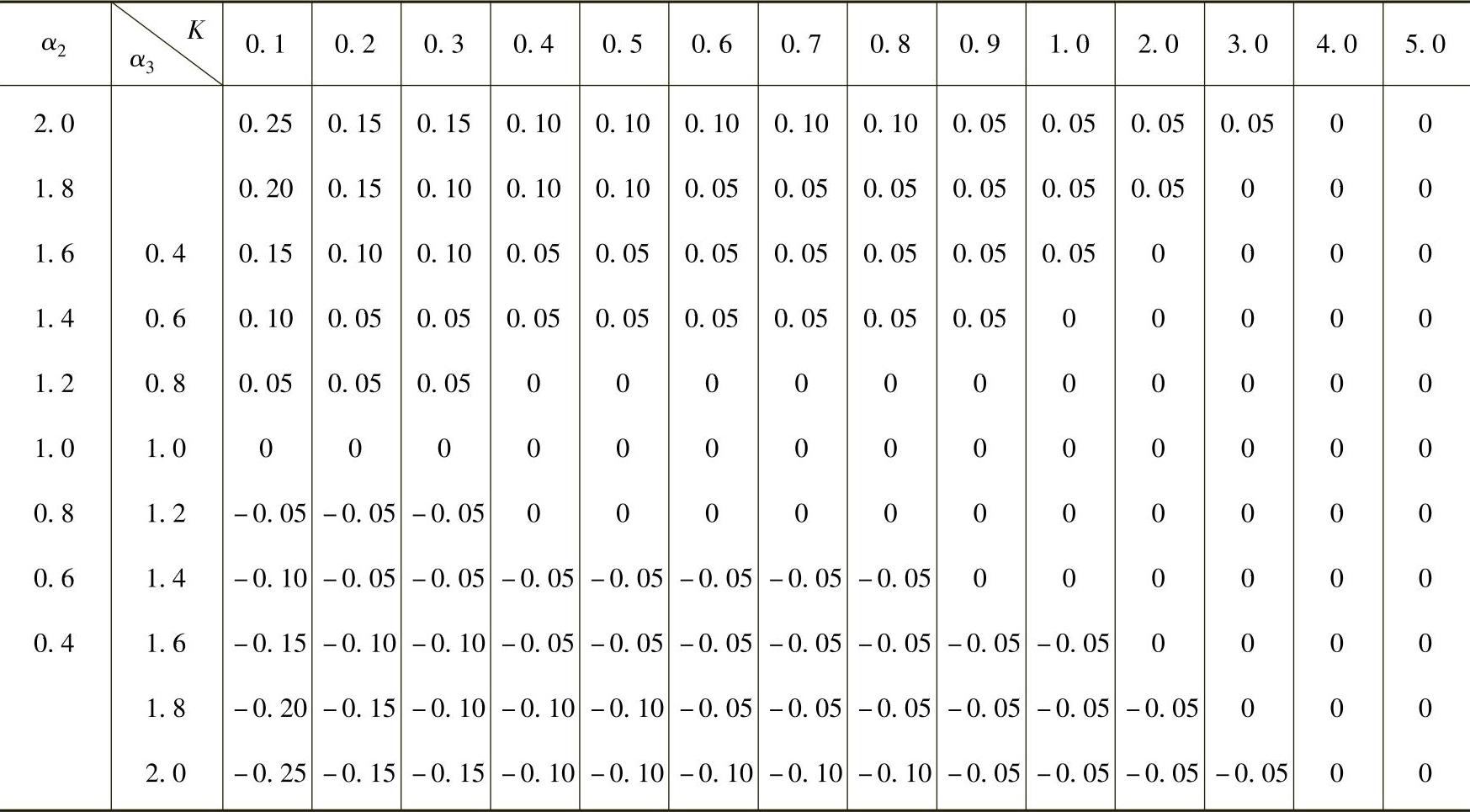
表4-7 上、下层层高度变化时反弯点高度比的修正值y2和y3
注: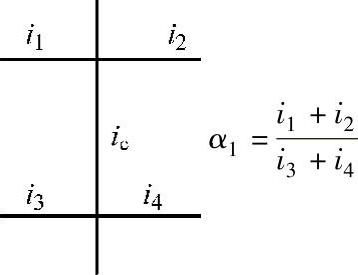 ,当i1+i2>i3+i4时,则α1取倒数,即
,当i1+i2>i3+i4时,则α1取倒数,即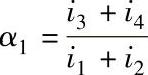 ,并且y1取负号;K按表4-3计算;底层可不考虑此项修正,即取y1=0。
,并且y1取负号;K按表4-3计算;底层可不考虑此项修正,即取y1=0。
注:α2=h上/h,α3=h下/h,h为计算层层高,h上为上一层层高,h下为下一层层高;K按表4-3计算;y2按K及α2查表,对顶层可不考虑该项修正;y3按K及α3查表,对底层可不考虑该项修正。
【例4-4】要求用D值法计算图4-22所示框架结构内力,框架计算简图中给出了水平力及各杆件的线刚度的相对值。
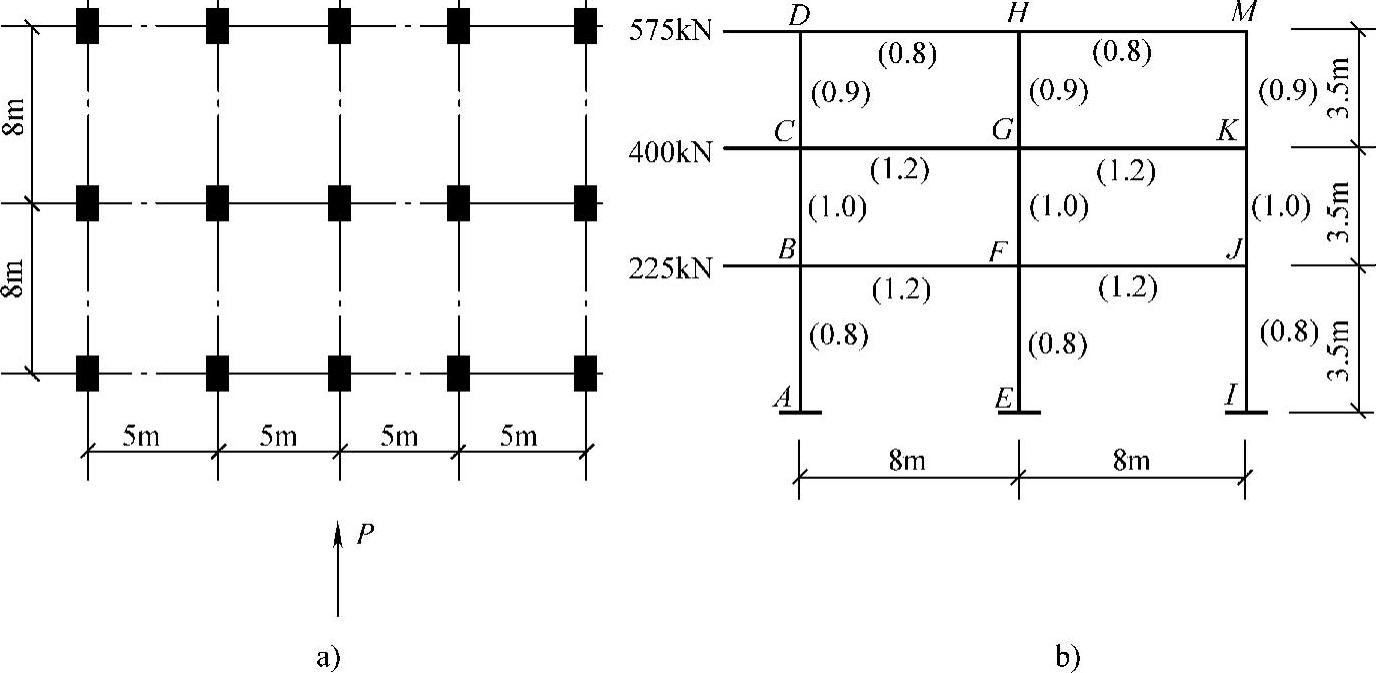
图4-22 框架结构平面布置及其计算简图
解:(1)计算层剪力Vi、Dij、Vij
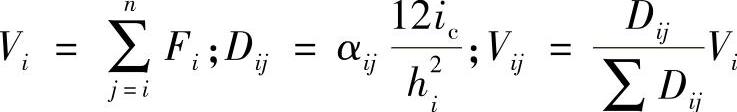
计算结果见表4-8。
(2)计算y(y=y0+y1+y2+y3)计算结果见表4-9。
表4-8 框架柱Dij、Vi、Vij值计算

表4-9 y值计算

(3)计算柱端弯矩
第三层:边柱 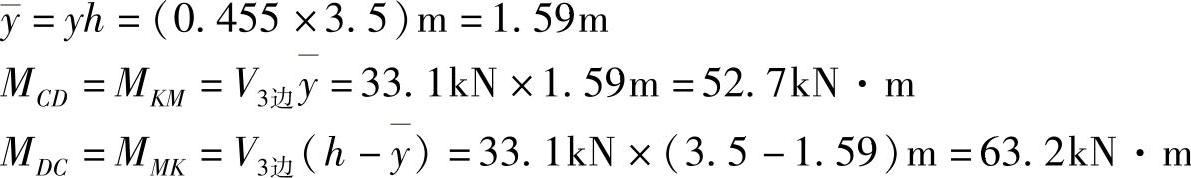
中柱 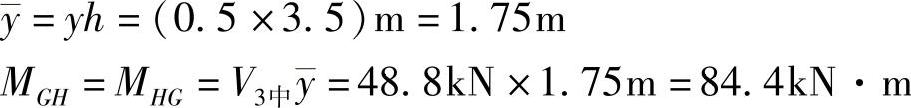
第二层:边柱 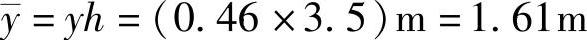
MBC=MJK=V2边y=56.4kN×1.61m=90.8kN·m
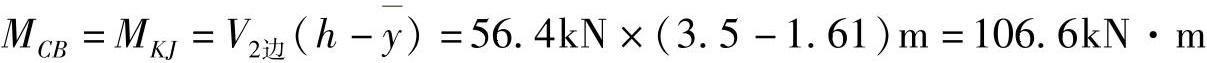
中柱 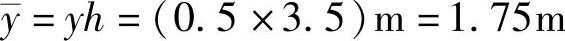
MFG=MGF=V2中y=82.1kN×1.75m=143.7kN·m
第一层:边柱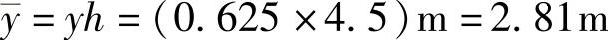
MAB=MIJ=V1边y=74.4kN×2.81m=209.1kN·m
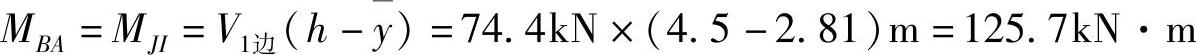
中柱 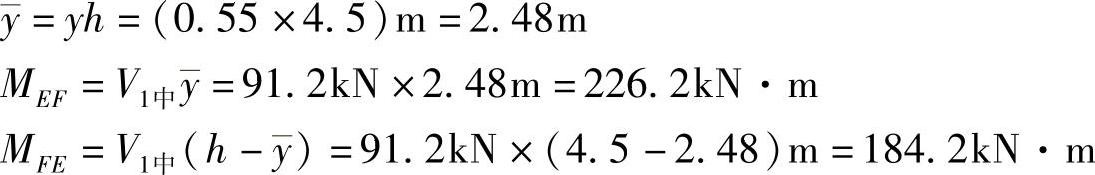
(4)计算梁端弯矩
第三层MDH=MMH=MDC=MMK=63.2kN·m
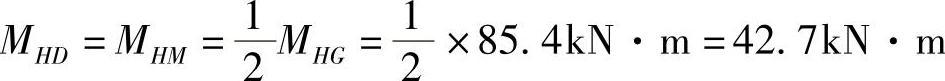
第二层MCG=MCD+MCB=MKG=(52.7+106.6)kN·m=159.3kN·m
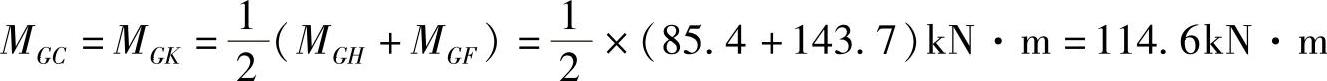
第一层 MBF=MBC+MBA=MJF=(90.8+125.7)kN·m=216.5kN·m
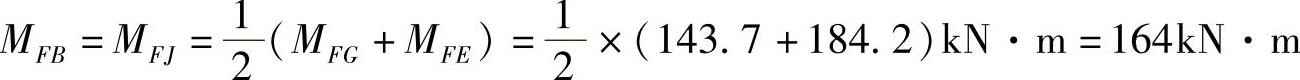
(5)画弯矩图 如图4-23所示。
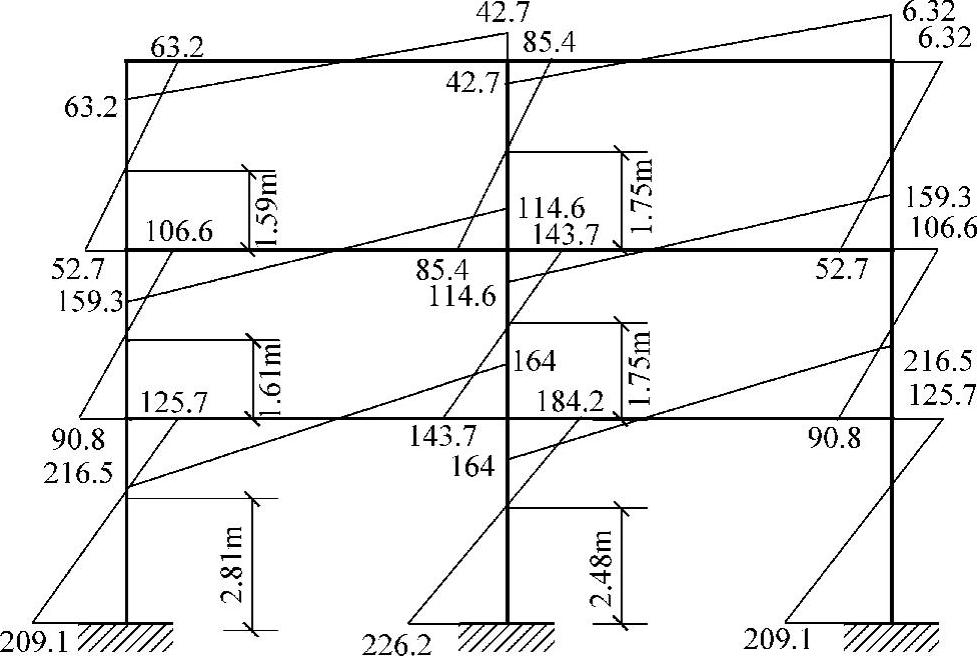
图4-23 例4-4弯矩图(单位:kN·m)
相关文章

三铰拱为静定结构,其全部支座反力和内力都可由平衡条件确定。图12-22竖向荷载作用下的三铰拱内力计算1.支座反力的计算三铰拱有四个支座反力。即拱的竖向反力与相应简支梁的竖向反力相同。试计算图12-23所示三铰拱的内力,并绘制其内力图。图12-24三铰拱内力图弯矩图;剪力图;轴力图......
2025-09-29

静定平面刚架的内力计算同梁一样,仍是用截面法截取隔离体,然后用平衡条件求解。根据荷载情况,将刚架分解成若干杆段,由平衡条件求出杆端内力。该杆上作用有一集中荷载,可以分为CE和EB两个无荷载区段,用截面法求出下列控制截面的弯矩:便可以绘制出该杆弯矩图。根据荷载和已经求出的反力,可以用截面法求出杆件各个控制截面的剪力和轴力,从而绘制出整个钢架的剪力图和轴力图,如图12-18、所示。......
2025-09-29

桁架的内力计算方法有节点法、截面法、联合法。桁架中某杆的轴力为零时,此杆称为零杆。图13-16试用节点法计算图13-17所示桁架的各杆内力。求图13-19所示桁架1、2、3杆的内力N1、N2、N3。如图13-20所示,欲求图中a杆的内力,如果只用节点法计算,无论取哪个节点为隔离体,都有三个以上的未知力,无法直接求解;如果只用截面法计算,也需要解联立方程。宜联合应用节点法和截面法,求所需反力和指定杆件内力。......
2025-09-30

设计荷载分基本荷载和特殊荷载两类。根据设计图确定。工作人员及浇筑设备、工具的荷载。计算模板及直接支承模板的楞木 (围囹)时,可按均布荷载2.5kPa 及集中荷载2.5kN 计算;计算支承楞木的构件时,可按1.5kPa计算;计算支架立柱时按1kPa计算。是侧面模板承受的主要荷载。表8-1最大侧压力pm值由表8-1 的侧压力分布图可知,它近似于一个三角形。根据现行GB 50009—2001 《建筑结构荷载规范》确定。......
2025-09-29

作用在多、高层建筑结构上的荷载有竖向荷载和水平荷载。竖向荷载按平面框架的负荷面积分配给各片平面框架,负荷面积按梁板布置情况确定。水平荷载一般简化为作用于框架节点的水平集中力,每片平面框架分担的水平荷载与它们的抗侧刚度有关。现结合多层框架结构房屋的特点,对楼面活荷载作一些补充说明。各种房屋或房间的楼面活荷载折减系数可由《建筑结构荷载规范》查得。......
2025-09-30

平面汇交力系可以建立两个独立的平衡方程,解算两个未知量。继续取8、6、7等结点为隔离体,可求得桁架右半边各杆的内力。图12-30桁架轴力示意在桁架内力计算时,往往会遇到内力为零的杆件,这种杆件称为零杆。计算桁架的内力宜从几何分析入手,以便选择适当的计算方法,灵活地选取隔离体和平衡方程。除结点法外,计算桁架内力的另一基本方法是截面法。截面法适用于联合桁架的计算以及简单桁架中求少数指定杆件内力的情况。......
2025-09-29

在短路电流的最简化计算中,可以假定短路电路连接到内阻抗为零的恒电势电源上。因此,短路电流周期分量的幅值不随时间而变化,只有非周期分量是衰减的。如果就上述短路电流的数值也不知道,那么还可以从与该部分连接的变电所装设的断路器的切断容量得到极限利用的条件来近似地计算系统的电抗。......
2025-09-29

第二个案例是在模拟地震荷载下混凝土柱的损伤演化致失效分析。图6.38混凝土柱试样[36]图6.39试验中施加的荷载谱应用前述的损伤演化致失效的跨尺度自适应模拟与分析方法对如图6.38所示的混凝土柱试样在试验模拟的地震荷载作用下的跨尺度损伤演化过程进行模拟,模拟结果见图6.40。通过将所模拟的混凝土柱在模拟地震荷载下的损伤演化过程的数值结果与实验结果进行对比,表明数值模拟结果与实验结果吻合较好,表明所发展的算法是可靠的。......
2025-09-30
相关推荐