框架结构承受的水平荷载主要是风荷载和水平地震作用。由图4-15b可知，规则框架在水平荷载作用下，在柱中弯矩均为直线，均有一零弯矩点，称为反弯点，若求得各柱反弯点位置和剪力，则柱的弯矩就可求。水平荷载作用下框架结构的内力和侧移可用结构力学方法计算，常用的近似算法有迭代法、反弯点法、D值法和门架法等。标准反弯点高度比是在等高、等跨，各层梁柱线刚度都不变的多层框架在水平荷载作用下求得的反弯点高度比。......
2023-08-30
混凝土结构设计：竖向荷载下内力近似计算的4.4.1框架结构
【摘要】：多层多跨框架在竖向荷载作用下，侧移很小，各层荷载对其他层杆件的内力影响不大，结构的内力可用力矩分配法计算。用力矩分配法计算各单层框架内力1）将框架分层以后，各单层框架柱的远端视为固定端。图4-10为二层框架结构，括号内数值为杆件相对线刚度，试利用分层法计算框架弯矩，并画出弯矩图。
框架结构简化为平面框架后，即可按照框架的负荷面积计算作用在框架上的竖向荷载。多层多跨框架在竖向荷载作用下，侧移很小，各层荷载对其他层杆件的内力影响不大，结构的内力可用力矩分配法计算。工程设计中，如采用手算，可采用迭代法、分层法、弯矩二次分配法及系数法等近似方法计算。本节简要介绍分层法及弯矩二次分配法的基本概念和计算要点。
1.计算假定
现在分析框架某层的竖向荷载对其他层的影响问题。由结构力学可知，等截面直杆远端固定时，弯矩传递系数为0.5，远端铰接时，弯矩传递系数为0。实际情况介于固定和铰接之间，因此，弯矩传递系数为0～0.5。首先，荷载在本层节点产生的不平衡力矩经过分配和传递，才影响本层杆件的远端。然后，在远端再进行分配才会影响到相邻层。在框架结构中，构件的远端一般与几个杆件相连，故传给远端的弯矩要在分配给相邻的各杆件后再向这几个杆件的远端传递，这样才能将弯矩传给其他层的梁和隔层的柱，这样第二次传递的弯矩就更小了，可忽略不计。
计算框架在竖向荷载作用下的内力时，可采用如下计算假定：
1）忽略框架在竖向荷载作用下的侧移。
2）作用在某一层梁上的竖向荷载只对本层梁以及与本层梁相连的柱产生弯矩和剪力，而对其他层的梁和隔层的柱不产生弯矩和剪力。
2.分层法
分层法就是依据计算假定，将一个n层框架分解成n个单层框架，每个单层框架用力矩分配法计算杆件内力。如图4-9a所示框架，可分解成如图4-9b所示的4个单层刚架。
图4-9 框架分层法计算简图
分层计算所得的梁端弯矩即为其最后弯矩。而每一柱（底层柱除外）属于上、下两层刚架，所以柱的弯矩为上、下两层弯矩相加。
分层计算时将柱的远端视为固定端，而实际结构中，除底层柱外，其他层柱端并不是固定端，在柱端有节点转角，柱的远端处于弹性约束状态。为考虑这一差别，应将除底层柱外的其他层柱的线刚度乘以0.9折减系数，并将传递系数取为1/3，底层柱的传递系数仍为1/2。
（1）用力矩分配法计算各单层框架内力
1）将框架分层以后，各单层框架柱的远端视为固定端。
2）计算各单层框架在竖向荷载作用下的梁固端弯矩。
3）计算梁、柱的线刚度和弯矩分配系数。
梁线刚度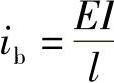 
，柱的线刚度
式中 I——梁、柱截面惯性矩；
l——梁跨度；
h——柱高。
计算梁截面惯性矩I时，对现浇楼盖：中间框架I=2I0，边框架I=1.5I0，I0是不考虑楼板影响时矩形梁的截面惯性矩。除底层柱外的其他层柱的线刚度乘以0.9折减系数，并将传递系数取为1/3。
（2）框架内力
1）用力矩分配法算得的各单层框架梁上的弯矩，即为所求框架梁的弯矩。将相邻两个单层框架中同一根柱的弯矩叠加，即得框架柱弯矩。此时，节点上的弯矩可能不平衡，必要时可将节点不平衡弯矩再分配一次。
2）根据杆端弯矩及梁上荷载求出框架剪力和轴力。
【例4-1】图4-10为二层框架结构，括号内数值为杆件相对线刚度，试利用分层法计算框架弯矩，并画出弯矩图。
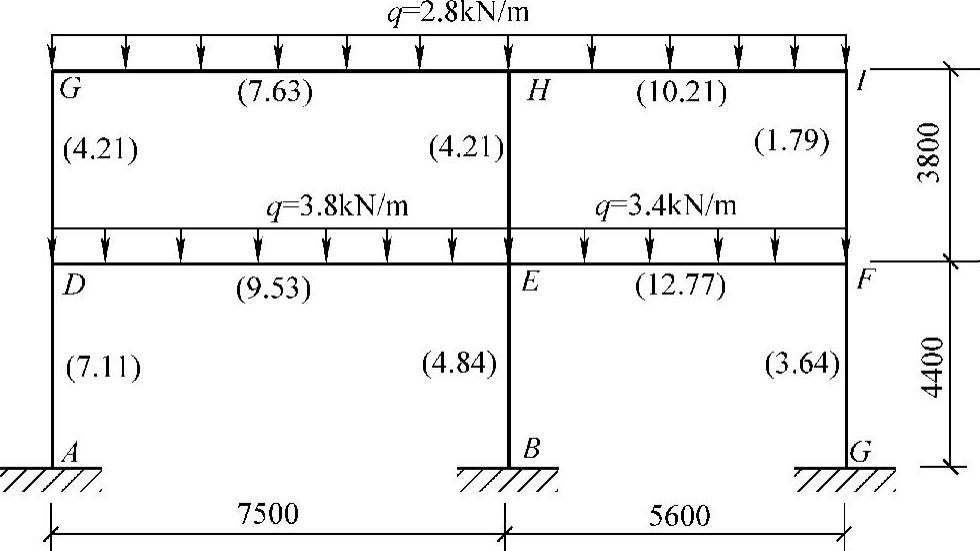
图4-10 框架计算简图
解：（1）求各节点的梁、柱弯矩分配系数，计算结果见表4-2。
表4-2 各层梁柱线刚度及弯矩分配系数计算
（2）固端弯矩计算
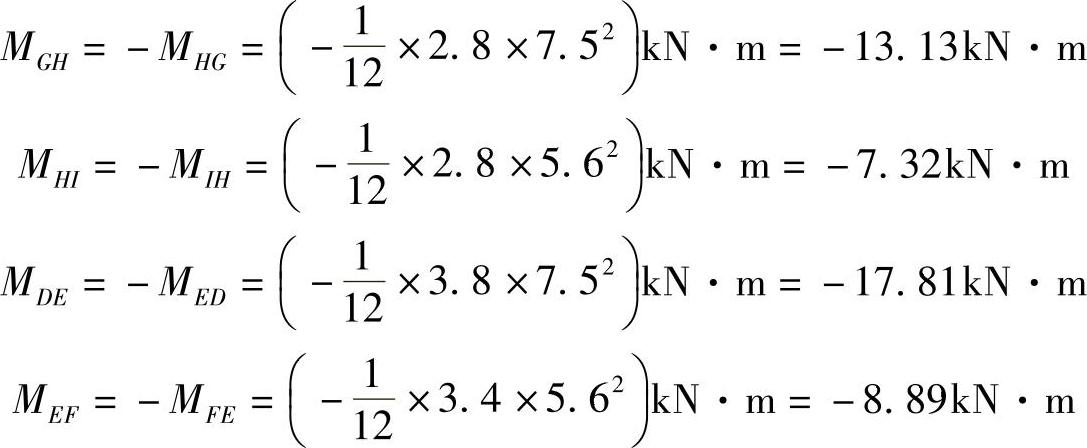
（3）分层法计算各节点弯矩 顶层及底层弯矩计算如图4-11、图4-12所示。
图4-11 顶层弯矩计算（单位：kN·m）
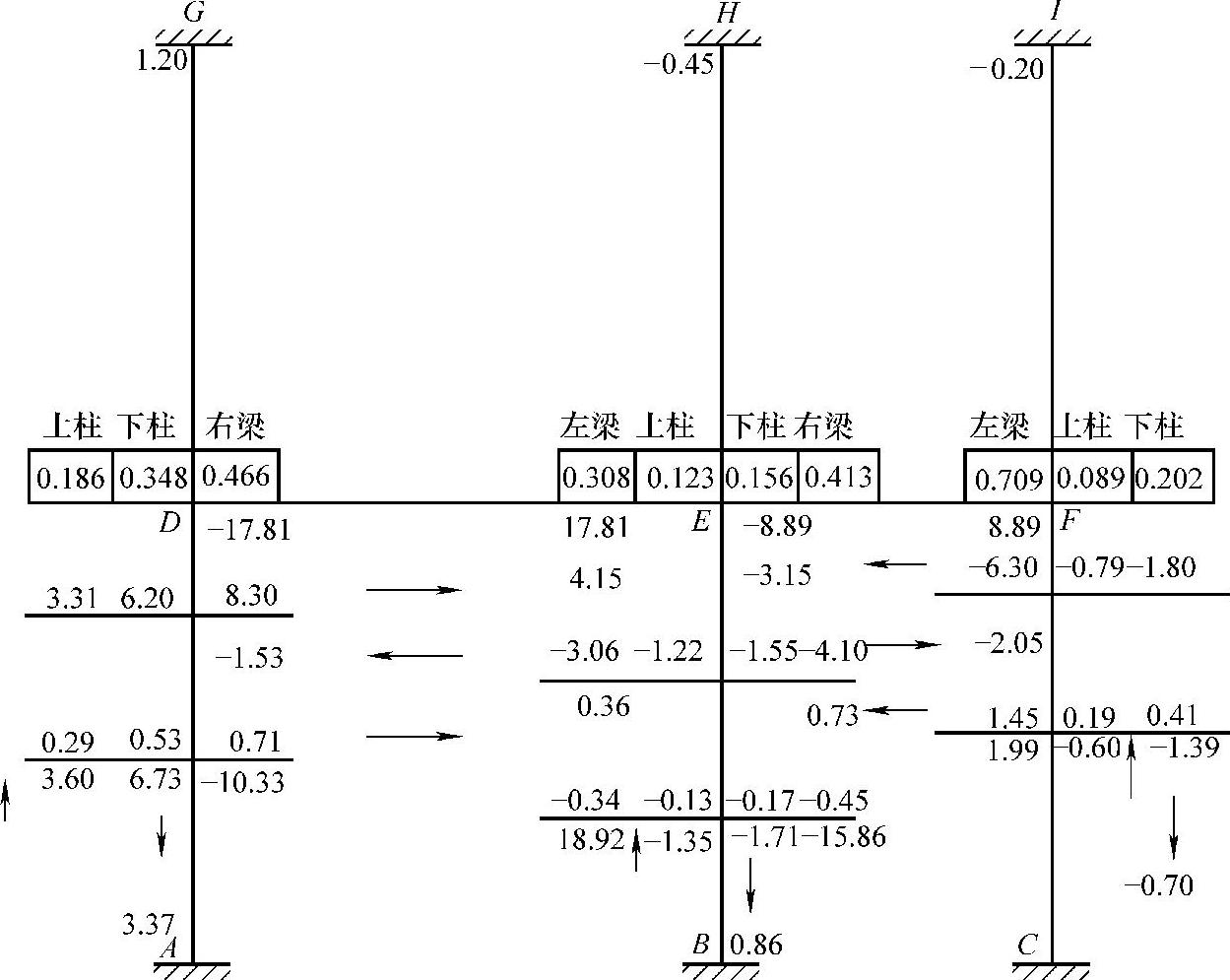
图4-12 底层弯矩计算（单位：kN·m）
（4）画弯矩图 同一层柱的柱端弯矩叠加后的弯矩图如图4-13所示。
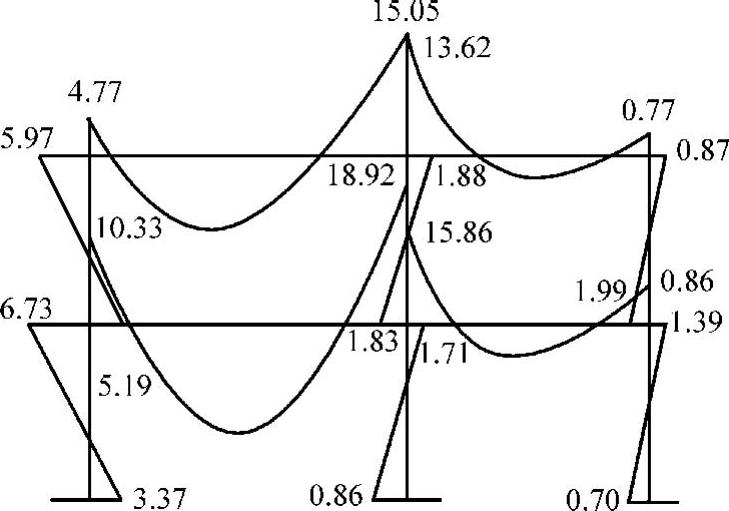
图4-13 例4-1框架弯矩图（单位：kN·m）
最后结点的不平衡弯矩可再进行分配，使节点弯矩达到平衡（其弯矩图略）。
（5）计算梁、柱端剪力（具体计算略）
（6）计算柱轴力（具体计算略）
Ni=Ni+1+Vi。
3.弯矩二次分配法
计算竖向荷载作用下多层多跨框架结构的杆端弯矩时，如用无侧移框架的弯矩分配法，由于该法要考虑任一节点的不平衡弯矩对框架结构所有杆件的影响，因而计算相当繁复。根据在分层法中所作的分析可知，多层框架中某节点的不平衡弯矩对相邻节点的影响较大，对其他节点的影响较小，因而可假定某一节点的不平衡弯矩只对与该节点相交的各杆件的远端有影响，这样可将弯矩分配法的循环次数简化到弯矩二次分配和其间的一次传递，此即弯矩二次分配法。
弯矩二次分配法是在满足工程计算精确度的条件下，对力矩分配法计算过程进行简化，框架不必分层，整体计算，所有节点同时分配力矩，又同时向远端传递，再将节点的不平衡再分配一次即完成。这种方法适合手算。
弯矩二次分配法计算要点：
1）计算各杆的线刚度：梁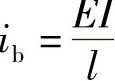
，柱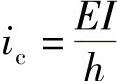
。
2）计算各杆固端弯矩和弯矩分配系数，计算弯矩分配系数时，柱的线刚度不折减。
3）将所有节点的固端弯矩同时反号分配（第一次分配）。
4）将各杆端的分配弯矩乘以1/2的传递系数同时向远端传递（第一次传递）。
5）将各节点传递弯矩和同时反号分配（第二次分配）。
6）将各杆端固端弯矩、分配弯矩、传递弯矩叠加，即为各杆端的最终弯矩。
【例4-2】已知框架同例4-1（见图4-10），试利用弯矩二次分配法计算其框架弯矩。
解：利用弯矩二次分配法计算，计算过程如图4-14所示。
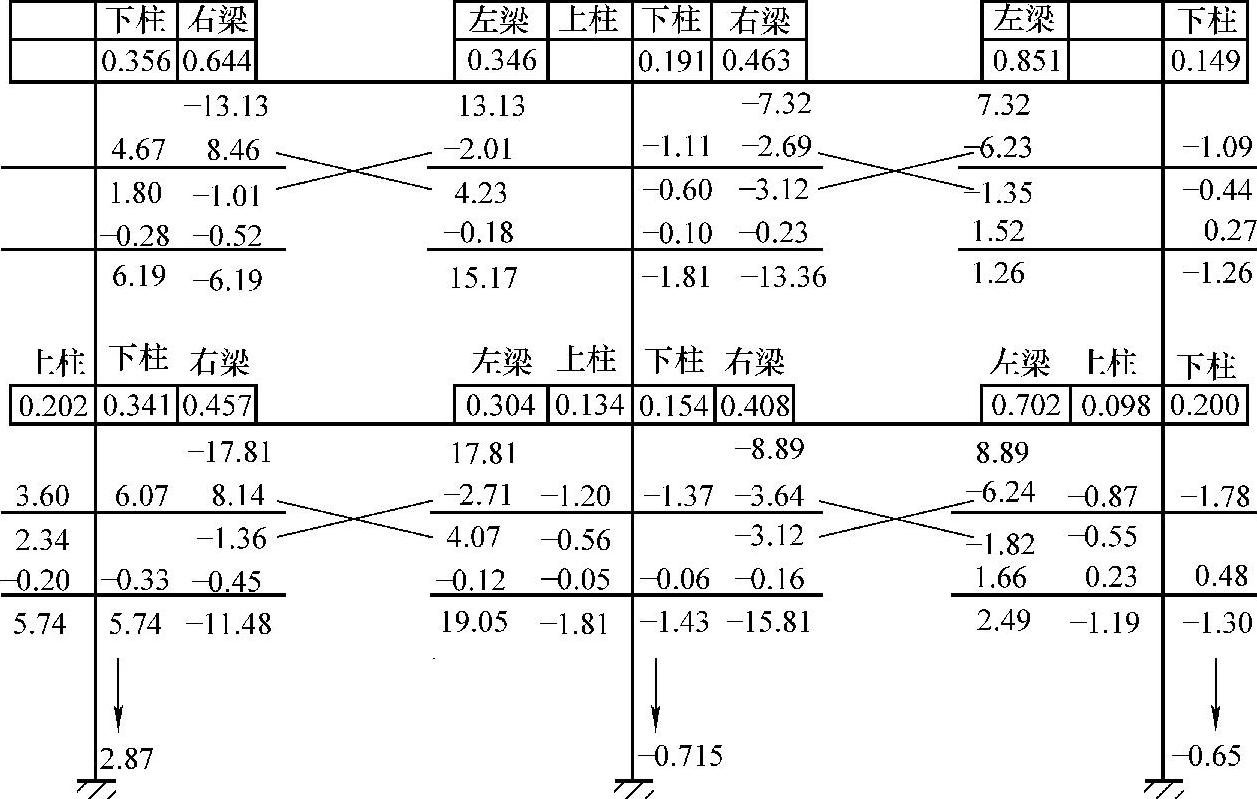
图4-14 例4-2弯矩二次分配法计算（单位：kN·m）
有关混凝土结构设计的文章
- 详细阅读
-
竖向荷载作用下三铰拱的内力计算详细阅读
三铰拱为静定结构，其全部支座反力和内力都可由平衡条件确定。图12-22竖向荷载作用下的三铰拱内力计算1.支座反力的计算三铰拱有四个支座反力。即拱的竖向反力与相应简支梁的竖向反力相同。试计算图12-23所示三铰拱的内力，并绘制其内力图。图12-24三铰拱内力图弯矩图；剪力图；轴力图......
2023-06-16
-
混凝土结构设计：4.4.3框架结构水平荷载下详细阅读
事实上，框架结构的侧移主要在水平荷载作用下产生，其侧移控制主要是结构的层间相对位移控制。图4-24 水平荷载下框架侧移1.梁柱弯曲变形引起的侧移如图4-24b所示，梁柱弯曲变形引起的侧移曲线属于剪切型变形，可用D值法来计算。对于高层框架，水平荷载产生的柱轴力较大，由柱轴力引起的侧移值也较大，在侧移计算中不可忽略。框架在水平荷载作用下，柱将产生轴向拉伸和压缩，框架因此产生弯曲型侧移。......
2023-08-30
-
4.3.3框架结构荷载分析|混凝土结构设计详细阅读
作用在多、高层建筑结构上的荷载有竖向荷载和水平荷载。竖向荷载按平面框架的负荷面积分配给各片平面框架，负荷面积按梁板布置情况确定。水平荷载一般简化为作用于框架节点的水平集中力，每片平面框架分担的水平荷载与它们的抗侧刚度有关。现结合多层框架结构房屋的特点，对楼面活荷载作一些补充说明。各种房屋或房间的楼面活荷载折减系数可由《建筑结构荷载规范》查得。......
2023-08-30
-
排架内力计算的结果-混凝土结构设计详细阅读
任意荷载作用下等高排架的内力计算，需要首先求解单阶超静定柱在各种荷载作用下的柱顶反力。图3-42 任意荷载作用下的等高排架内力分析2.不等高排架的内力计算不等高排架在任意荷载作用下，由于高、低跨的柱顶移位不相等，因此，不能用剪力分配法求解，通常用力法进行分析。下面以图3-43a所示两跨不等高排架为例，说明其内力计算方法。解力法方程求得未知力x1、x2后，就可通过平衡条件求得该两跨不等高排架各柱的内力。......
2023-08-30
-
混凝土结构设计-排架内力组合详细阅读
排架结构内力组合是将排架柱在各单项荷载作用下的内力，按照它们在使用过程中同时出现的可能性进行组合。在对钢筋混凝土结构构件进行裂缝宽度验算时，应采用荷载效应的准永久组合；在进行地基承载力验算时，应采用荷载效应的标准组合。为此，需要确定可能的最不利弯矩和轴力组合。对不考虑抗震设防的排架柱，箍筋一般由构造控制，故在柱的截面设计时，可不考虑最大剪力对应的不利内力组合，以及其他不利内力组合对应的剪力值。......
2023-08-30
-
混凝土结构设计中的排架荷载计算详细阅读
对两跨排架，考虑活荷载出现的可能性，屋面每跨在均布活荷载作用下的计算简图如图3-35所示。4）起重机荷载使吊车梁产生扭矩，因此，要计算扭矩并进行扭曲截面承载力验算。图3-36 起重机竖向荷载计算简图起重机竖向荷载......
2023-08-30
-
肋梁楼盖荷载传递原则-混凝土结构设计详细阅读
图2-3 交叉梁的荷载传递图2-4 荷载传递原则a）EI1=EI2时，P1/P和P2/P随跨度比L2/L1的变化 b）L1=L2时，P1/P和P2/P随抗弯刚度比EI1/EI2的变化2.单向板与双向板首先考虑图2-5a所示仅两对边简支的矩形板。根据上述荷载传递原则，板面荷载沿板短跨方向传递程度要大于沿长跨方向的传递程度。......
2023-08-30
相关推荐