本小节介绍钢筋混凝土屋架的设计要点，其内容主要包括：屋架高度和截面尺寸的确定、荷载及其组合、内力分析、杆件截面设计及构造要求、屋架的扶起和吊装验算等。实际上，钢筋混凝土屋架的节点具有一定的刚性，并非理想铰接；此外，在按连续梁计算上弦杆弯矩时，假定支座为不动铰支座，而实际上屋架节点是有位移的。......
2023-08-30
混凝土结构设计要点：3.6.2吊车梁设计
【摘要】：吊车梁是厂房的主要承重构件，承受起重机的起吊、运行时产生的移动荷载；同时对传递纵向水平荷载、加强厂房纵向刚度起着重要作用。图3-56 内力影响线、可能的荷载不利布置及内力包络图吊车梁的每一截面，根据移动荷载组的间距和荷载值，都可计算出它的最大内力。图3-56c为两台起重机作用下吊车梁的弯矩包络图和剪力包络图。由弯矩包络图可见，梁的绝对最大弯矩截面靠近跨中的左右两侧。
吊车梁是厂房的主要承重构件，承受起重机的起吊、运行时产生的移动荷载；同时对传递纵向水平荷载、加强厂房纵向刚度起着重要作用。本小节介绍起重机梁的设计要点，其内容主要包括：截面尺寸的确定、内力计算和截面验算等。
1.截面尺寸的确定
吊车梁的截面一般设计成I形或T形、截面高度与起重机起重量有关，一般取h=（1/10～1/5）l，l为吊车梁的高度。吊车梁的上翼缘承受横向制动力产生的水平弯矩，翼缘宽度bf′=（1/15～1/10）l，翼缘厚度取hf′=（1/10～1/7）h。腹板厚度由抗剪和配筋构造要求确定，一般取腹板高度的1/7～1/4。I形截面的下翼缘宜小于上翼缘，由布置预应力筋的构造决定。
2.内力计算
除具有一般简支梁的受力特点外，吊车梁在内力计算方面还具有下列特殊性。
（1）在一组移动荷载作用下梁的绝对最大内力 吊车梁在一组移动荷载作用下，任一指定截面I—I（见图3-56a）的最大内力可用影响线原理求得。将各集中力Pi分别作用在I—I截面上（见图3-56b），并根据影响线求出相应的内力值，其中最大者就是该截面在这组移动荷载下的最大内力，相应于最大内力的荷载位置称为该截面的荷载最不利位置。
图3-56 内力影响线、可能的荷载不利布置及内力包络图
吊车梁的每一截面，根据移动荷载组的间距和荷载值，都可计算出它的最大内力。将各截面的最大内力连接起来即为内力包络图，它是设计吊车梁的主要依据。图3-56c为两台起重机作用下吊车梁的弯矩包络图和剪力包络图。
由弯矩包络图可见，梁的绝对最大弯矩截面靠近跨中的左右两侧。为找出绝对最大弯矩的截面位置，应先确定一组已知荷载的合力P所在位置（见图3-57）；若梁的中线平分此合力和相邻一集中力的间距时，则此集中力所在位置的截面就可能出现绝对最大弯矩。图3-57中的梁有两种可能，应分别计算其界面间距，选其中较大者作为此梁的绝对最大弯矩。
（2）横向弯矩和剪力 吊车梁在横向制动力作用下发生横向弯曲，其受力状态可视为在水平截面内工作的简支梁。可用起重机竖向荷载作用下相同的分析方法，求得吊车梁的最大横向弯矩和最大横向剪力。
（3）截面扭矩 起重机竖向轮压和横向水平制动力对吊车梁截面的弯曲中心均存在偏心距（见图3-58），故每个起重机轮子作用于吊车梁的扭矩mT为
mT=0.7（μPmaxe1+Te2） （3-29）
图3-57 求绝对最大弯矩时移动荷载的位置
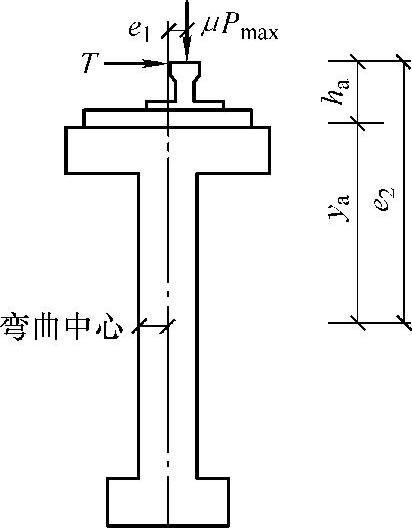
图3-58 吊车梁的扭矩
在疲劳强度验算时，不考虑横向水平制动力的作用，则
mT=0.8μPmaxe1 （3-30）
由于截面扭矩影响线与剪力影响线相同，故吊车梁的绝对最大扭矩发生在靠近支座截面处，可由剪力影响线求得总扭矩MT；
MT=∑mTiyi （3-31）
上述各式中，0.7和0.8为扭矩和剪力共同作用时的组合值系数；e1为轨道安装偏差，一般取20mm；e2为T的作用线对吊车梁截面弯曲中心的偏心距e2=ha+ya；ha为轨道顶面至吊车梁顶面的距离；ya为吊车梁顶面至弯曲中心的距离，可按材料力学有关公式计算；yi为各mT对应剪力影响线的坐标值。
3.截面验算
吊车梁是一种受力复杂的双向弯、剪、扭构件，且在使用阶段对其承载力、刚度和抗裂性要求较高，故需要按表3-6所示的内容进行验算。具体计算方法可参阅相关资料。
表3-6 吊车梁截面验算项目
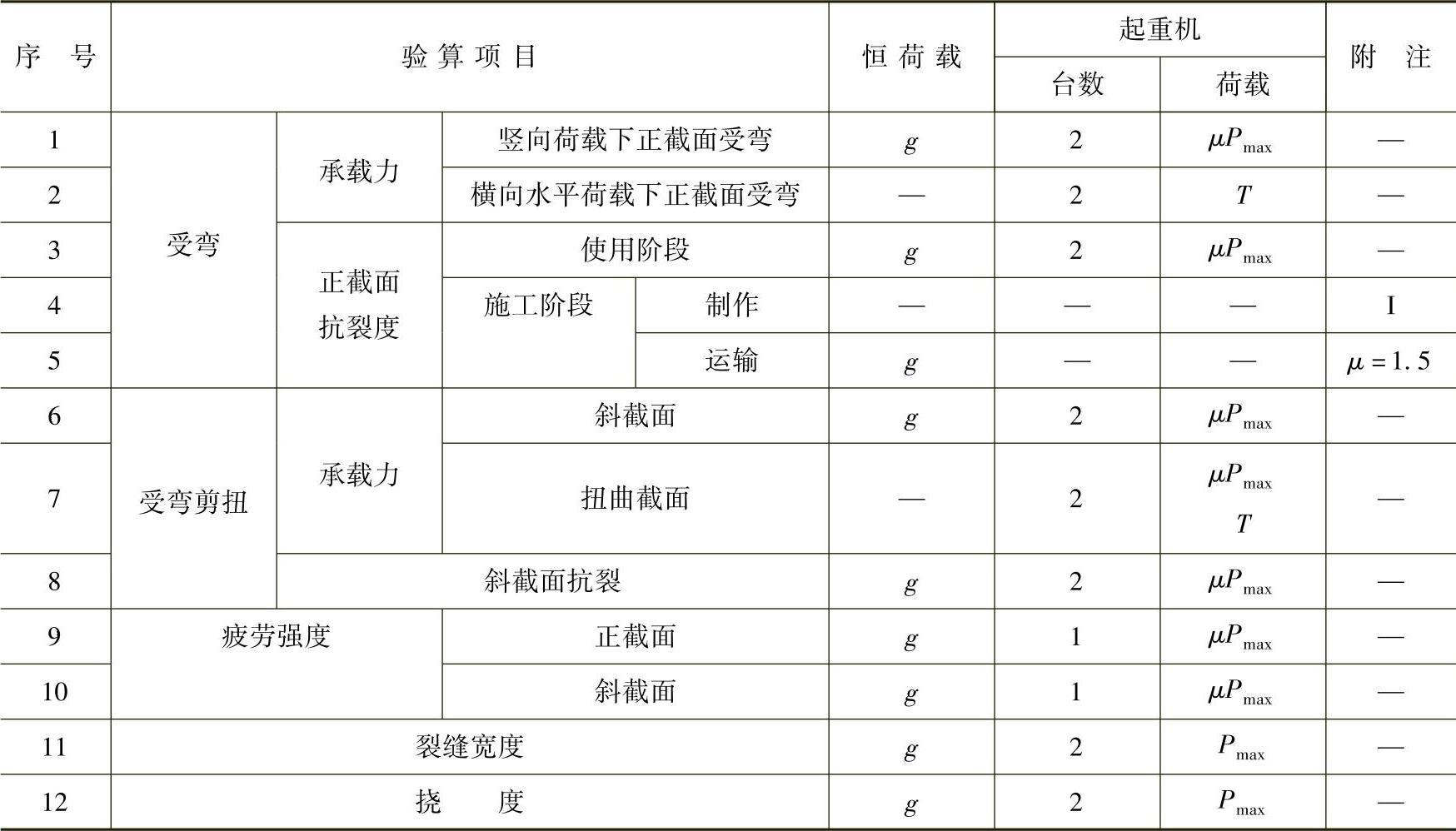
注：1.g为恒荷载，包括吊车梁及轨道连接件的重力荷载；Pmax为起重机最大轮压；T为起重机横向水平制动力；μ为动力系数。
2.表格中I代表当为预应力混凝土吊车梁时，要进行预应力混凝土构件制作时相应的验算。
有关混凝土结构设计的文章
- 详细阅读
- 详细阅读
-
混凝土楼梯结构设计-混凝土结构设计详细阅读
楼梯的平面布置、踏步尺寸、栏杆形式等由建筑设计确定，楼梯的结构形式则由结构设计确定。图2-74 整体式楼梯结构形式a）梁式 b）板式 c）剪刀式 d）螺旋式梁式楼梯由踏步板、梯段斜梁、平台板和平台梁组成。平台板支承于平台梁和墙体上，但是为了保证墙体安全，中间缓台平台板不宜支承于两侧墙体上。板式楼梯的优点是梯段板下表面平整，支模简单；其缺点是梯段板跨度较大时，斜板厚度较大，结构材料用量较多。......
2023-08-30
-
混凝土结构设计中凸出屋面天窗架横向抗震计算要详细阅读
4）凸出屋面天窗架的横向抗震计算，可采用下列方法：①有斜撑的三铰拱式钢筋混凝土和钢天窗架的横向抗震计算可采用底部剪力法，跨度大于9m或9度时，混凝土天窗架的地震作用效应应乘以增大系数，其值可采用1.5；②其他情况下天窗架的横向水平地震作用可采用振型分解反应谱法。......
2023-08-30
-
混凝土结构设计要求-混凝土结构设计详细阅读
框架结构属于高次超静定结构，荷载的形式与大小及构件的刚度都是框架内力和变形的决定因素，框架梁、柱截面尺寸应根据承载力、刚度及延性等要求确定。抗震设计时，梁端箍筋加密区箍筋的最小直径、最大间距应满足表4-14的要求；当梁端纵向钢筋配筋率大于2%时，表中箍筋直径应增大2mm。非抗震设计时，框架梁的箍筋应符合《混凝土结构设计规范》的规定。表4-15 柱纵向钢筋最小配筋率（%）注：1.表中括号内数值适用于框架结构。......
2023-08-30
-
预应力混凝土结构设计原理详细阅读
为了避免钢筋混凝土结构的裂缝过早出现，充分利用高强度钢筋及高强度混凝土，可以设法在结构构件受荷载前，用预压的办法来减小或抵消荷载所引起的混凝土拉应力，甚至使其处于受压状态。现以图8.2所示预应力混凝土简支梁为例，说明预应力混凝土结构的基本原理。图8.2预应力混凝土简支梁在荷载作用之前，预先在梁的受拉区施加偏心压力N，使梁下边缘混凝土产生预压应力为σc，梁上边缘产生预拉应力σct，如图8.2所示。......
2023-09-19
-
柱截面设计-混凝土结构设计成果详细阅读
对下柱，截面的有效高度取h0=mm=860mm，则大偏心受压和小偏心受压界限破坏时对应的轴压力为Nb=α1fc[bh0ξb+hf′]=1.0×14.3×[100×860×0.518××150]kN=1280.54kN当N≤Nb=1280.54kN时，为大偏心受压；由表3-15～表3-17可见，下柱Ⅱ—Ⅱ和Ⅲ—Ⅲ截面共有24组不利内力。由表3-5查得有起重机厂房排架方向上柱的计算长度为lc=l0=2×3.9m=7.8m；由表3-12可计算得出上柱截面的回转半径i=115.4mm。则M=ηsM2=kN·m=118.52kN·m故取x=2as′进行计算。......
2023-08-30
-
混凝土柱截面设计，结构设计成果详细阅读
当偏心受压柱的截面高度h≥600mm时，在侧面应设置直径不于10mm的纵向构造钢筋，并相应地设置复合箍筋或拉筋。当柱截面短边尺寸大于400mm且纵向钢筋多于3根时，或当柱截面短边尺寸不大于400mm且各边纵向钢筋多于4根时，应设置复合箍筋。......
2023-08-30
相关推荐