排架结构内力组合是将排架柱在各单项荷载作用下的内力,按照它们在使用过程中同时出现的可能性进行组合。在对钢筋混凝土结构构件进行裂缝宽度验算时,应采用荷载效应的准永久组合;在进行地基承载力验算时,应采用荷载效应的标准组合。为此,需要确定可能的最不利弯矩和轴力组合。对不考虑抗震设防的排架柱,箍筋一般由构造控制,故在柱的截面设计时,可不考虑最大剪力对应的不利内力组合,以及其他不利内力组合对应的剪力值。......
2023-08-30
1.等高排架内力计算
等高排架是指各柱的柱顶标高相等,或柱顶标高虽不相等,但柱顶由倾斜横梁相连的排架,如图3-39所示。由于排架横梁可视为刚性连杆,故等高排架在任意荷载作用下各柱柱顶侧移相等,因此可按剪力分配法求出各柱的柱顶剪力。这样超静定排架的内力计算问题就转变为静定悬壁柱在已知柱顶剪力和外荷载作用下的内力计算。任意荷载作用下等高排架的内力计算,需要首先求解单阶超静定柱在各种荷载作用下的柱顶反力。
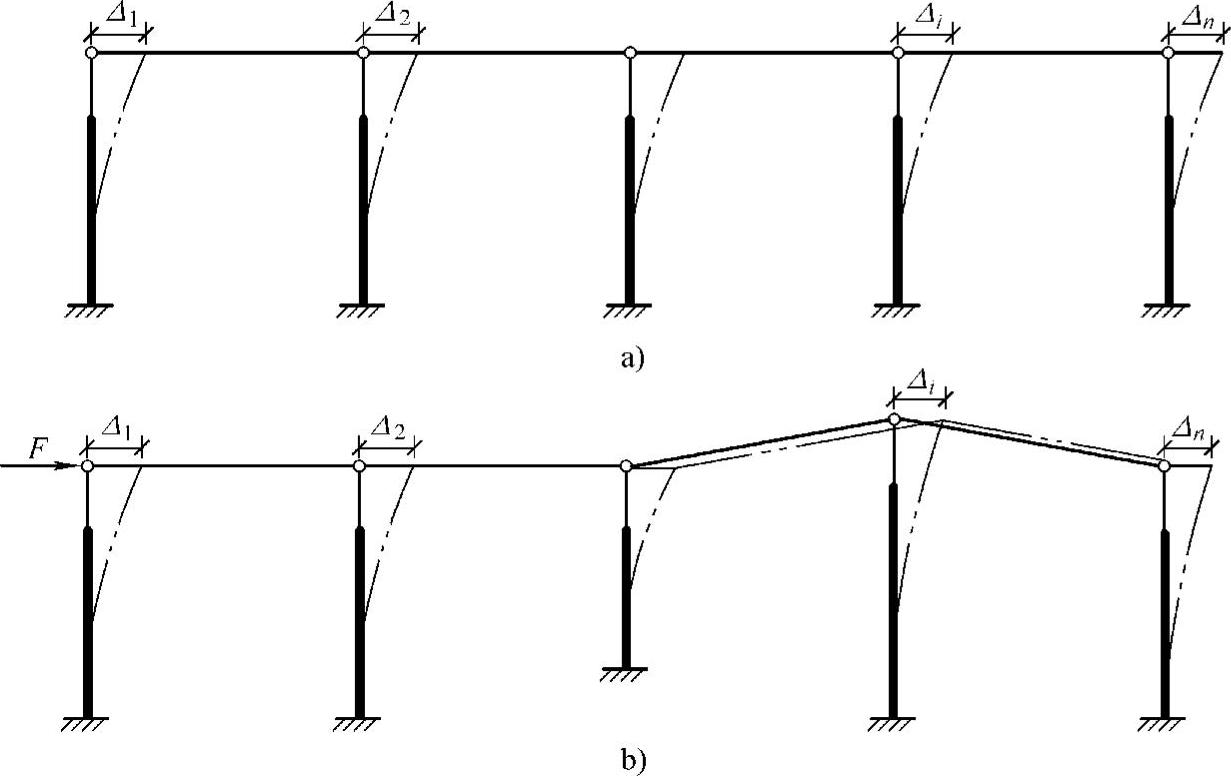
图3-39 等高排架计算简图
(1)单阶一次超静定柱在任意荷载作用下的柱顶反力 单阶一次超静定柱为柱顶不动铰支、下端固定的单阶变截面柱,如图3-40a所示。这是一个用力法对变截面构件求解的问题。如在变截面处作用一力矩M时,设柱顶反力为R,取基本体系如图3-40b所示,由力法方程可得Rδ-ΔP=0,则

式中 δ——悬臂柱在柱顶单位水平力作用下柱顶处的侧移值,因其主要与柱的形状有关,故称为形常数;
ΔP——悬壁柱在荷载作用下柱顶处的侧移值,因与荷载有关,故称为载常数。
由式(3-13)可见,柱顶不动铰支座反力R等于柱顶处的载常数除以该处的形常数。
令λ=Hu/H,n=Iu/Il,由图3-40c、图3-40d、图3-40e,根据结构力学中的图乘法可得

将式(3-14)和式(3-15)代入式(3-13),得

式中 C0——单阶变截面柱的柱顶位移系数,按式(3-17)计算;
CM——单阶变截面柱在变阶处集中力矩作用下的柱顶反力系数,按式(3-18)计算。
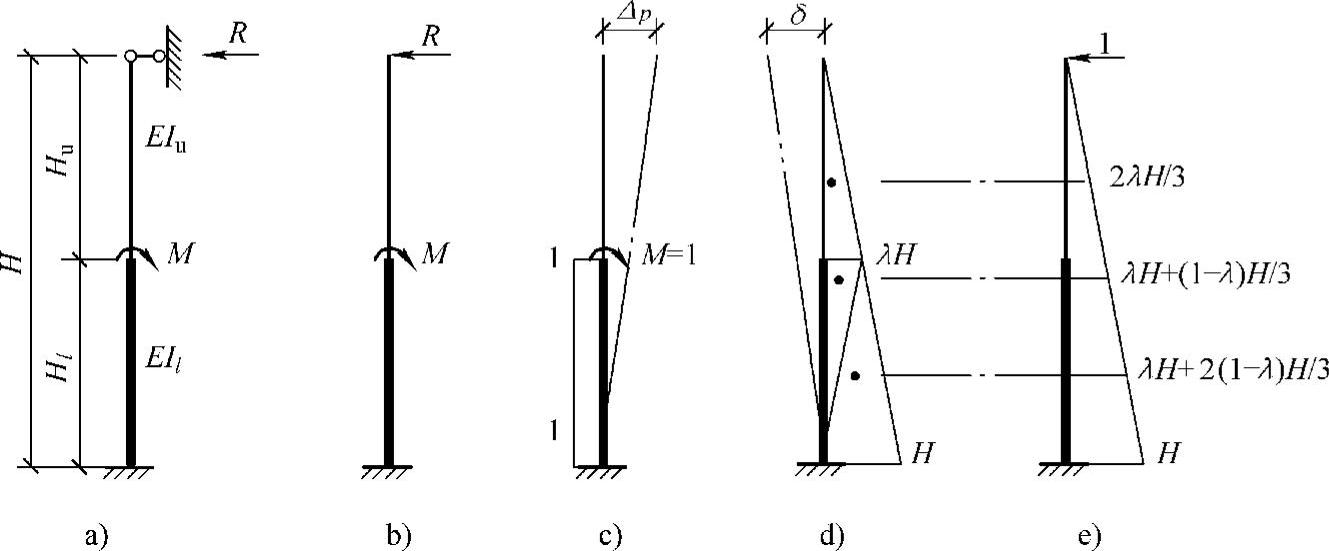
图3-40 单阶一次超静定柱分析
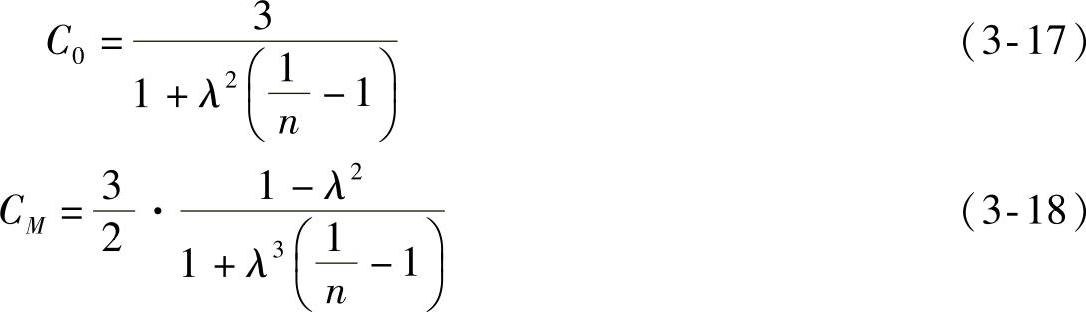

图3-41 柱顶水平集中力作用下的等高排架内力分析
按照上述方法,可得到单阶变截面柱在各种荷载作用下的柱顶反力系数。表3-2列出了单阶变截面柱的柱顶位移系数C0及在各种荷载作用下的柱顶反力系数C1~C11。
(2)柱顶水平集中力作用下等高排架内力分析 如图3-41a所示,在柱顶水平集中力F作用下,等高排架各柱顶将产生侧移Δi,由于假定横梁为无轴向变形的刚性连杆,故有下列变形条件
Δ1=Δ2=…=…=Δn=Δ (Ⅰ)
若沿横梁与柱的连接处将各柱的柱顶切开,则在各柱顶的切口上作用有一对相应的剪力Vi,如图3-41a所示。如取出横梁为脱离体,则有下列平衡条件
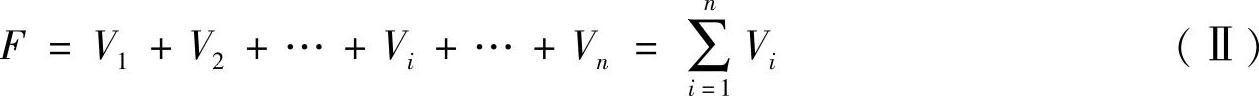
此外,根据形常数δi的物理意义,可得下列物理条件(图3-41b):
表3-2 单阶变截面柱的柱顶位移系数C0和反力系数C1~C11
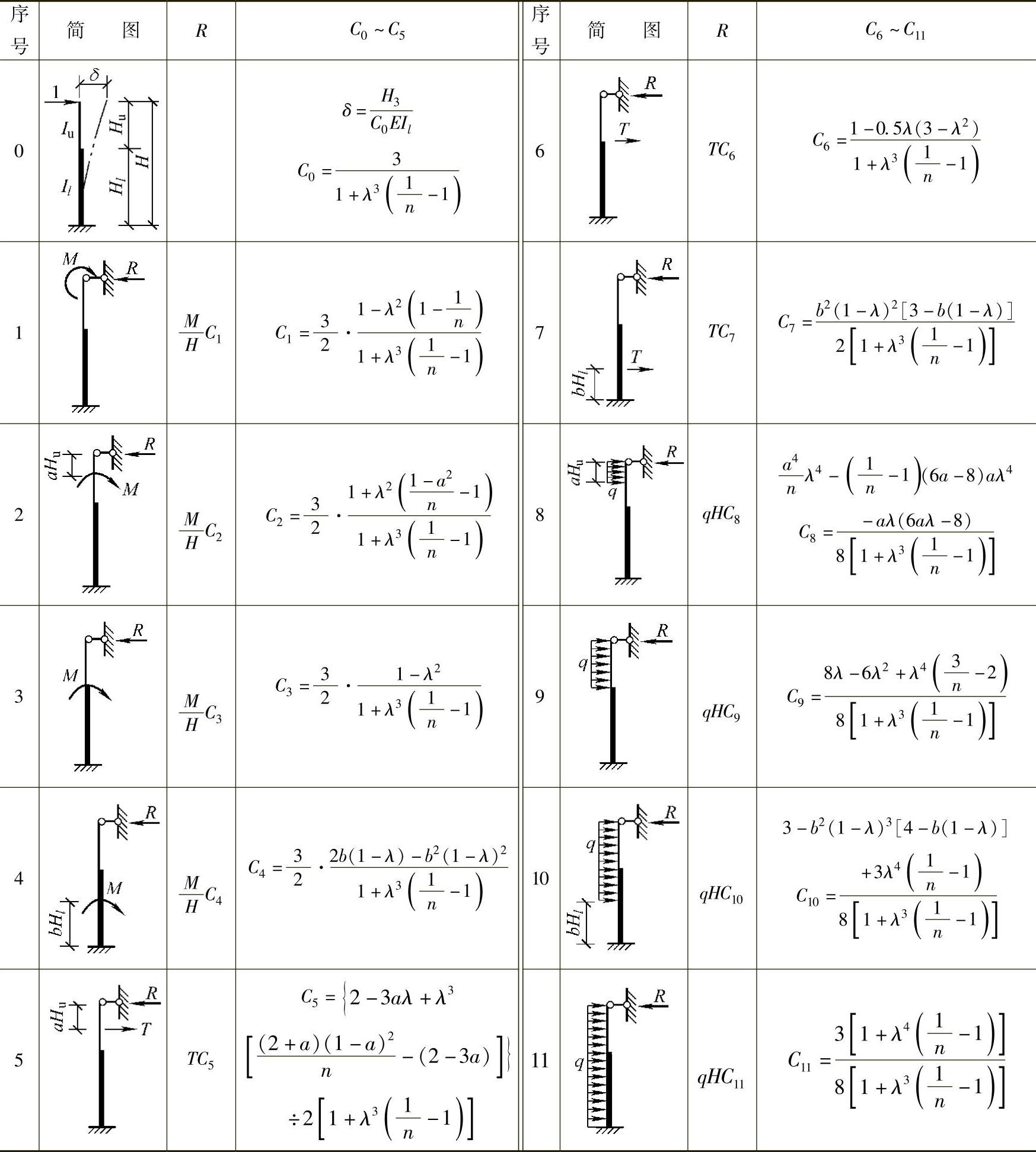
注:表中n=Iu/Il,λ=Hu/H,1-λ=Hl/H。
Viδi=Δi (Ⅲ)
联立方程(Ⅱ)和(Ⅲ)求解,并利用式(Ⅰ)的关系,可得

式中 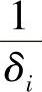 ——第i根排架柱的抗侧移刚度(或抗剪刚度),即悬壁柱柱顶产生单位侧移所需施加的水平力;
——第i根排架柱的抗侧移刚度(或抗剪刚度),即悬壁柱柱顶产生单位侧移所需施加的水平力;
ηi——第i根排架柱的剪力分配系数,按下式计算

按式(3-19)求得柱顶剪力后,根据平衡条件即可求得排架柱各截面的弯矩和剪力。
(3)任意荷载作用下等高排架的内力计算 等高排架在任意荷载作用下的内力计算步骤如下:
1)对承受任意荷载作用的排架(见图3-42a),在排架柱顶部附加一个不动铰支座以阻止其侧移,则各柱为单阶一次超静定柱(见图3-42b)。应用柱顶反力系数可求得各柱反力及相应的柱端剪力,得到柱顶假想的不动铰支座总反力为R=∑Ri。在图3-42b中,R2为零,R=R1+R3。
2)撤除假想的附加不动铰支座,将支座总反力R反向作用于排架柱顶(见图3-42c),应用剪力分配法可求出柱顶水平力R作用下各柱顶剪力ηiR。
3)将图3-42b、图3-42c的计算结果叠加,可得到在任意荷载作用下排架柱顶剪力Ri+ηiR,如图3-42d所示,根据此图即可求出各柱的内力。

图3-42 任意荷载作用下的等高排架内力分析
2.不等高排架的内力计算
不等高排架在任意荷载作用下,由于高、低跨的柱顶移位不相等,因此,不能用剪力分配法求解,通常用力法进行分析。下面以图3-43a所示两跨不等高排架为例,说明其内力计算方法。
图3-43b所示为不等高排架的基本构造,未知力为x1、x2,可列力法方程如下

式中 δ11、δ12、δ21、δ22——基本结构的柔度系数,可由图3-43c、图3-43d的单位力弯矩图图乘得到;
Δ1P、Δ2P——载常数,可分别由图3-43c、图3-43e以及图3-43d、图3-43e图乘得到。
解力法方程(3-21)求得未知力x1、x2后,就可通过平衡条件求得该两跨不等高排架各柱的内力。

图3-43 任意荷载作用下的等高排架内力分析
3.考虑厂房整体空间作用的排架内力计算
(1)厂房整体空间作用的概念 当结构布置或荷载分布不均匀时,由于屋盖等纵向联系构件将各榀排架或山墙联系在一起,故各榀排架或山墙的受力及变形都不是单独的,而是互相制约的。这种排架与排架、排架与山墙之间的相互制约作用,称为厂房的整体空间作用。单层厂房整体空间作用的程度主要取决于屋盖的水平刚度、荷载类型、山墙刚度和间距等因素。因此,无檩屋盖比有檩屋盖、局部荷载比均匀荷载、有山墙比无山墙的厂房的整体空间作用要大些,对于一般单层厂房,在恒荷载、屋面活荷载、雪荷载以及风荷载作用下,按平面排架结构分析内力时,可不考虑厂房的整体空间作用;而起重机荷载仅作用在几榀排架上,属于局部荷载,故在起重机荷载作用下按平面排架结构分析内力时,需考虑厂房的整体空间作用。
(2)起重机荷载作用下考虑厂房整体空间作用的排架内力分析
如图3-44a所示的单层厂房,当某一榀排架柱顶作用水平集中力R时,若不考虑厂房的整体空间作用,则此集中力R完全由直接承受荷载的排架承受,其柱顶水平位移为Δ(见图3-44c);当考虑厂房的整体空间作用时,由于相邻排架的协同工作,柱顶水平集中力R不仅由直接承受荷载的排架承受,而且将通过屋盖等纵向联系构件传给相邻的其他排架,使整个厂房共同承受荷载,如果把屋盖看作一根在水平面内受力的梁,而各榀横向排架作为梁的弹性支座(见图3-44b),则各支座受力R即为相应排架所分担的水平力。
厂房空间作用的大小可通过空间分配系数μ来反映。表示当水平荷载作用于排架顶柱时,由于厂房结构的空间作用。该排架分配到的水平荷载与不考虑空间作用按平面排架计算分配到的水平荷载的比值。μ值越小,说明厂房的空间作用越大,反之则越小。如设直接承受荷载的排架对应的支座反力为R0,且在弹性阶段,排架顶柱的水平位移与其所受荷载成正比,则空间作用分配系数可表示如下

式中 Δ0——考虑空间作用时直接受荷排架的柱顶位移。
表3-3给出了起重机荷载作用下单跨厂房的μ值,可供设计时参考。由于厂房在吊车荷载作用下并不是只有单个集中荷载作用,而是同时有多个集中荷载作用,故表中的数值考虑了这个问题并留有一定的安全储备。
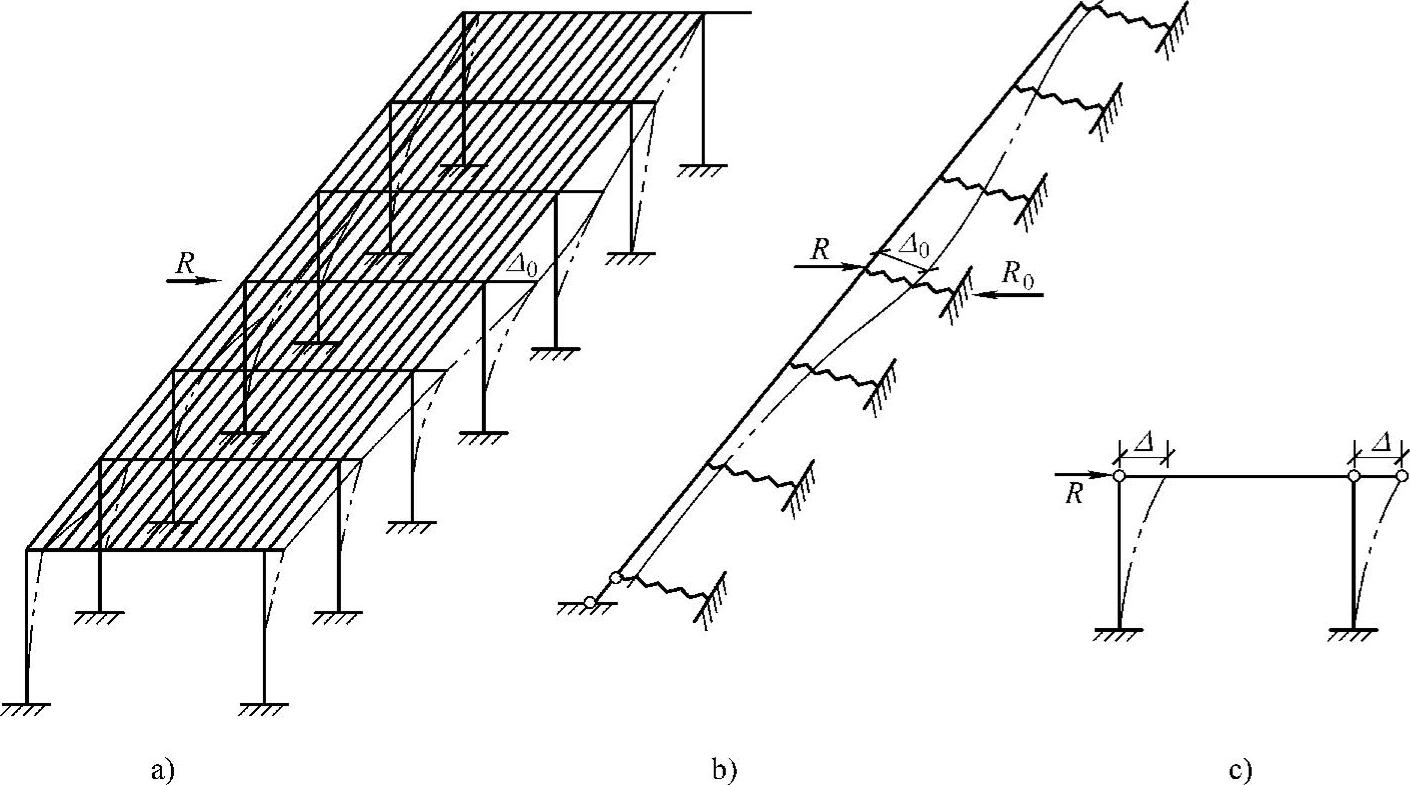
图3-44 厂房整体空间作用分析
表3-3 单跨厂房空间作用分配系数μ
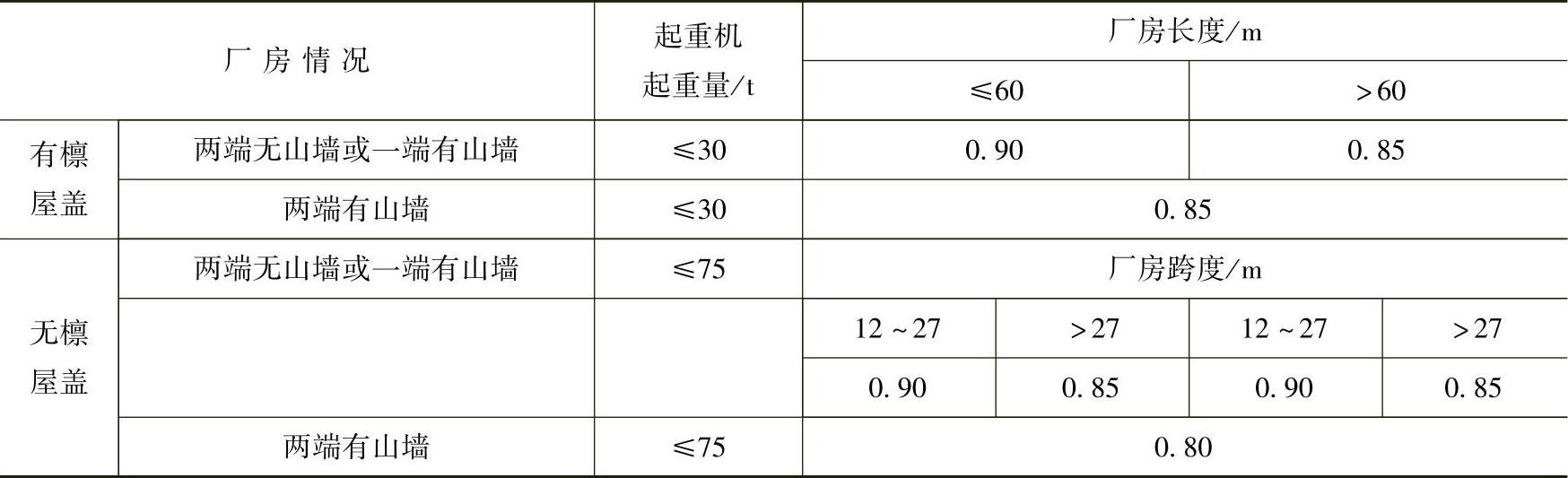
注:1.厂房山墙应为实心砖墙,洞口对山墙水平截面面积的削弱应不超过50%,否则应视为无山墙情况。
2.当厂房没有伸缩缝时,厂房长度应按一个伸缩缝处理,应视为无山墙。
(3)考虑厂房整体空间作用时排架内力的计算步骤 对于图3-45a所示排架,当考虑厂房整体空间作用时,可按下述步骤计算排架内力:
1)先假定排架柱顶无侧移,求出在起重机水平荷载Tmax作用下的柱顶反力R(或RA、RB)以及相应的柱顶剪力(见图3-45b),R=RA+RB。
2)将柱顶反力R乘以空间作用分配系数η,并将它反方向施加于该榀排架的顶柱,按剪力分配法求出各柱顶剪力ηAμR、ηBμR(见图3-45c)。

图3-45 考虑空间作用时排架内力分析
3)将上述两项计算求得的柱顶剪力叠加,即为考虑空间作用的顶柱剪力,根据顶柱剪力及柱上实际承受的荷载,按静定悬臂柱可求出各柱的内力,如图3-45d所示。
由图3-45d可见,考虑厂房整体空间作用时,柱顶剪力为
Vi′=Ri-ηiμR
不考虑厂房整体空间作用时(μ=1.0),柱顶剪力为
Vi=Ri-ηiR
由于u<1.0,故Vi′>Vi。因此,考虑厂房整体空间作用时,上柱内力将增大;又因为Vi′与Tmax方向相反,所以下柱内力将减小。由于下柱的配筋量一般比较多,故考虑空间作用后,柱的钢筋总用量有所减少。
有关混凝土结构设计的文章

排架结构内力组合是将排架柱在各单项荷载作用下的内力,按照它们在使用过程中同时出现的可能性进行组合。在对钢筋混凝土结构构件进行裂缝宽度验算时,应采用荷载效应的准永久组合;在进行地基承载力验算时,应采用荷载效应的标准组合。为此,需要确定可能的最不利弯矩和轴力组合。对不考虑抗震设防的排架柱,箍筋一般由构造控制,故在柱的截面设计时,可不考虑最大剪力对应的不利内力组合,以及其他不利内力组合对应的剪力值。......
2023-08-30

图3-64 恒载作用下排架内力图2.屋面活荷载作用下排架内力分析AB跨作用屋面活荷载 排架计算简图如图3-65a所示。其中起重机竖向荷载Dmax、Dmin在牛腿顶面外引起的力矩分别为MA=Dmaxe3=kN·m=138.68kN·mMB=Dmine3=kN·m=72.56kN·m对于A柱,C3=1.104,则对于B柱,n=0.218,λ=0.305,由表3-2得排架各柱顶剪力分别为VA=RA-ηAR=kN=-10.60kN(←)VB=RB-ηBR=kN=9.24kN(→)VC=-ηCR=kN=1.36kN(→)排架各柱的弯矩图、轴力图及柱底剪力值如图3-67b、c所示。......
2023-08-30

合并后平面排架柱的惯性矩应按合并考虑。图中排架柱的高度由基础顶面算至柱顶,其中,Hu表示上柱高度,Hl表示下柱高度。排架柱的计算轴线均取上、下柱截面的形心线。当柱为变截面柱时,排架柱的计算轴线呈折线形,如图3-33b所示。......
2023-08-30

对两跨排架,考虑活荷载出现的可能性,屋面每跨在均布活荷载作用下的计算简图如图3-35所示。4)起重机荷载使吊车梁产生扭矩,因此,要计算扭矩并进行扭曲截面承载力验算。图3-36 起重机竖向荷载计算简图起重机竖向荷载......
2023-08-30

图4.18按照抗剪要求计算各截面所需弯起钢筋的数量对于跨中截面:故不需设置剪力钢筋的区段长度。表4.4各排弯起钢筋起弯点设计弯矩计算表根据表4.4所示各截面设计弯矩值Mdx绘制设计弯矩图。图4.19按抗弯承载力要求计算各排弯起钢筋起弯......
2023-09-19

前面讲过,截面弯曲刚度就是使截面产生单位曲率需要施加的弯矩值。把式、式和式、式代入Bs的基本表达式中,即得短期截面弯曲刚度Bs的计算公式:式中,当h′f>0.2 h0时,取h′f=0.2 h0计算。式适用于矩形、T形、倒T形和工形截面受弯构件,由该式计算的平均曲率与试验结果符合较好。③当其他条件相同时,截面有效高度h0对截面弯曲刚度的影响最显著。......
2023-09-19

多层多跨框架在竖向荷载作用下,侧移很小,各层荷载对其他层杆件的内力影响不大,结构的内力可用力矩分配法计算。用力矩分配法计算各单层框架内力1)将框架分层以后,各单层框架柱的远端视为固定端。图4-10为二层框架结构,括号内数值为杆件相对线刚度,试利用分层法计算框架弯矩,并画出弯矩图。......
2023-08-30

2)梁内钢筋布置及种类纵向受力钢筋梁内主钢筋通常放在梁的底部承受拉应力,是梁的主要受力钢筋。梁内纵向受力钢筋直径一般选用10~30 mm,一般不超过40 mm,以满足抗裂要求。钢筋混凝土T梁的架立钢筋直径多为22 mm,矩形截面梁一般为10~14 mm。图3.5梁内钢筋骨架3)梁内钢筋保护层为使钢筋免于锈蚀,主钢筋至构件边缘的净距应符合规范规定。梁内钢筋的位置排布及间距要求如图3.6所示。其中,h0,h,as释义详见本章3.3.3节。......
2023-09-19
相关推荐