双向板按弹性理论的分析方法在混凝土结构设计中的应用

2023-08-30 理论教育版权反馈

【摘要】：当板厚远小于板短边尺寸的1/30，且板的挠度远小于板厚时，双向板可按弹性薄板理论计算。对于跨内截面弯矩值，尚应考虑双向弯曲对两个方向板带弯矩值的相互影响。图2-40 连续双向板的计算图式

1.单区格双向板的内力及变形计算

精确计算双向板的内力比较复杂。当板厚远小于板短边尺寸的1/30，且板的挠度远小于板厚时，双向板可按弹性薄板理论计算。附录C中列出了六种不同边界条件的板在均布荷载作用下的弯矩及挠度系数。计算时，取单位板宽b=1000mm，根据边界条件和短跨与长跨的比值，可直接查出弯矩系数，按下式算得相应的弯矩值

m=表中系数×pl²₀₁ （2-42）

式中 m——双向板单位板宽中央板带跨内或支座处截面最大弯矩设计值（kN·m/m）；

p——板上作用的均布荷载设计值（kN/m²）；

l₀₁——短跨方向的计算跨度（m），计算方法与单向板的计算相同。

需要说明的是，附录C中的系数是根据材料的泊松比ν=0制定的。对于跨内截面弯矩值，尚应考虑双向弯曲对两个方向板带弯矩值的相互影响。当ν≠0时，跨内截面弯矩可按下式计算

m^ν₁=m₁+νm₂ （2-43）

m₂^ν=m₂+νm₁ （2-44）

式中 m^ν₁、m₂^ν——考虑双向弯曲相互影响后的l₀₁、l₀₂方向单位宽度板带的跨内弯矩设计值；

m₁、m₂——按ν=0计算的l₀₁、l₀₂方向单位宽度板带的跨内弯矩设计值；

ν——泊松比，对于混凝土ν=0.2。

对于支座截面弯矩值，由于另一个方向板带弯矩为零，故不存在两个方向板带弯矩的相互影响问题。

2.多区格等跨连续双向板的内力及变形计算

精确计算连续双向板内力较为复杂，因此工程中采用实用计算法，该法通过对双向板上可变荷载的最不利布置以及支承情况等的合理简化，将多区格连续板转化为单区格板，然后通过查单区格板内力系数表来进行计算，方法简单实用。

此法假定支承梁不产生竖向位移且不受扭，同时规定双向板沿同一方向相邻跨度的比值l_0min/l0max≥0.75，以免计算误差过大。

在确定活荷载的最不利作用位置时，采用了既接近实际情况又便于利用单区格板计算表的布置方案：当求支座负弯矩时，楼盖各区格板均满布活荷载；当求跨中正弯矩时，在该区格及其前后左右每隔一区格布置活荷载，即棋盘式布置，如图2-40所示。

（1）各区格板跨内截面最大弯矩值为了求某区格板跨内截面最大弯矩，活荷载按图2-40所示的棋盘式布置。为了利用单区格双向板的内力计算系数表，将这种荷载分布情况分解成各跨满布荷载g+q/2和间隔布置±q/2两种情况，按以下方法进行内力计算：

1）多区格双向板在荷载g+q/2作用下，由于内区格板中间支座两侧荷载相同，忽略远跨荷载的影响，可以近似地认为支座不转动或发生很小的转动，可将所有中间支座近似地看作固定支座，所有中间区格均可视为四边固定的双向板。

2）多区格双向板在荷载±q/2作用下，相邻区格板在支座处的转角方向一致，大小相同，中间支座的弯矩为零或很小，故可近似地将中间支座视为简支支座，从而中间各区格板均可视为四边简支的双向板。

对上述两种情况，利用单区格双向板的内力系数表可以方便地求出各区格板的跨内截面弯矩。

3）将各区格板在两种荷载作用下的跨内弯矩叠加，得到各区格板的跨内截面最大弯矩。

对于边、角区格板，跨内截面最大弯矩仍采用上述方法计算，但外边界条件按实际情况确定。

（2）各区格板支座截面最大负弯矩值求支座最大弯矩时，为了简化计算，假定恒荷载和活荷载都满布连续双向板所有区格，中间支座均视为固定支座，内区格板均可按四边固定的双向板计算其支座弯矩。对于边、角区格，外边界条件应按实际情况考虑。由相邻区格板分别求得的同一支座的负弯矩不相等时，取绝对值较大的作为该支座的最大负弯矩。

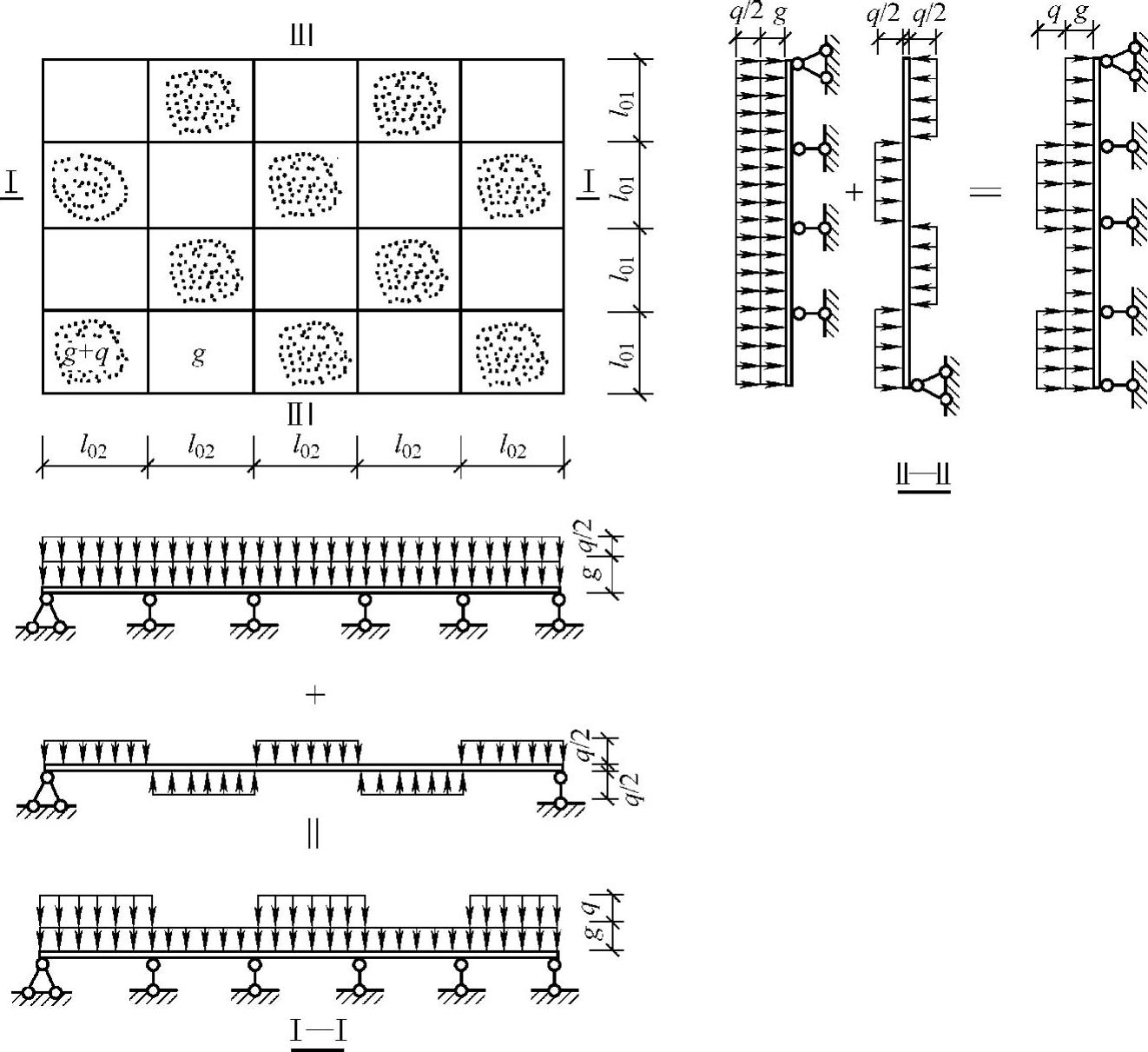
图2-40 连续双向板的计算图式

双向板按弹性理论的分析方法在混凝土结构设计中的应用

相关推荐