四边支承双向板的受力特点及试验结果

2023-08-30 理论教育版权反馈

【摘要】：本节主要讲述四边支承的正方形板和矩形板。图2-38 四边简支方板的主弯矩变化图2-39 均布荷载下双向板的裂缝分布

在纵、横两个方向弯曲且都不能忽略的板称为双向板。双向板的支承形式可以是四边支承、三边支承、两邻边支承或四点支承；板的平面形状可以是正方形、矩形、圆形、三角形或其他形状。本节主要讲述四边支承的正方形板和矩形板。

1.四边支承板弹性工作阶段的受力特点

如图2-37所示，从四边支承板内截出的任意两个板带并不是孤立的，它们受到相邻板带的约束，这使得其实际的竖向位移和弯矩有所减小。两个相邻板带的竖向位移是不相等的，靠近双向板边缘的板带，其竖向位移比靠近中央的相邻板带的竖向位移小，可见在相邻板带之间必定存在着竖向剪力。这种竖向剪力构成了扭矩。对此，还可以从图2-37中微元体（图中1234所示范围）的变形情况来理解：34面的曲率比12面小，两者间有相对扭转角存在，故在12、34面上必有扭矩作用；同理，在l₀₂方向的23面与14面也有扭矩。

扭矩的存在减小了按独立板带计算的弯矩值。与用弹性薄板理论求得的弯矩值进行比较，也可将双向板的弯矩计算简化为按独立板带计算出的弯矩乘以小于1的修正系数来考虑扭矩的影响。

与材料力学中由正应力、剪应力确定主应力的大小和方向相似，由l₀₁、l₀₂方向的弯矩M₁、M₂及扭矩M₁₂可确定主弯矩M_Ⅰ和M_Ⅱ及其方向

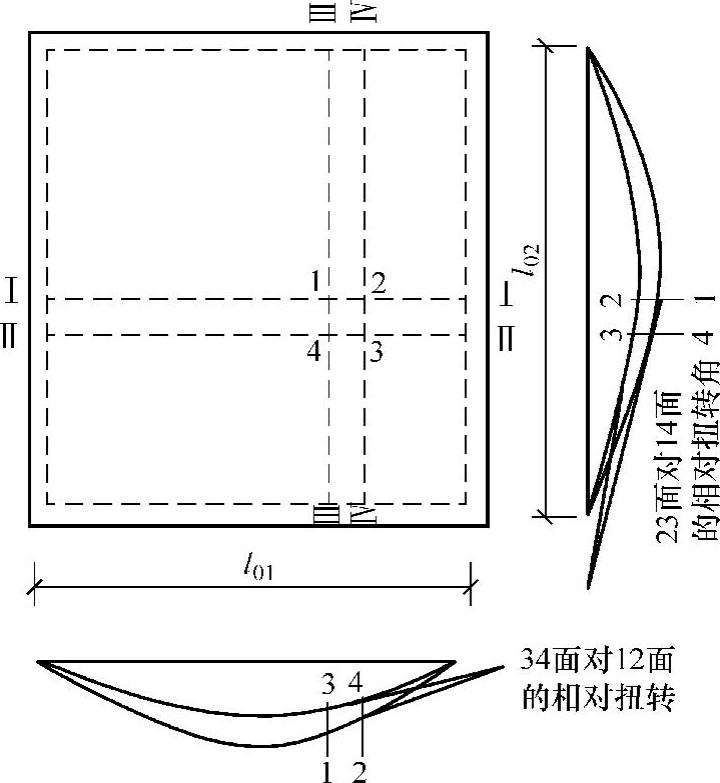
图2-37 双向板中的扭转变形

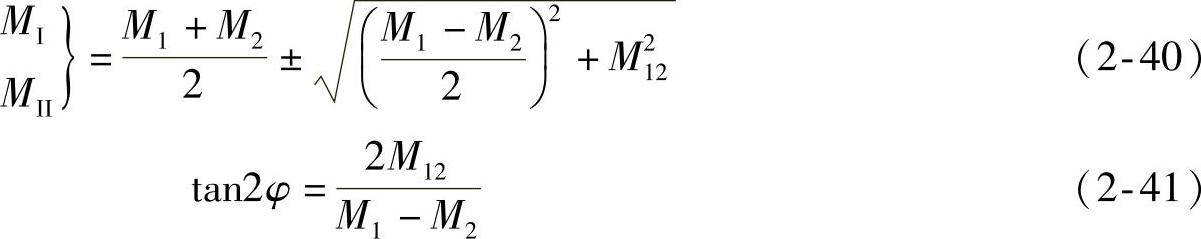
式中 M_Ⅰ、M_Ⅱ——两个相互垂直的主弯矩；

φ——主弯矩作用平面与l₀₁方向的夹角。

对于正方形板，由于对称，板的对角线上没有扭矩，故对角线平面就是主弯矩平面。图2-38为均布荷载p作用下，四边简支跨度为l的正方形板对角线上主弯矩的变化图形以及板中心线上弯矩M₁（=M₂）的变化图形（假定泊松比为零）。当用矢量表示时，主弯矩M_I的矢量是与对角线相平行的，且都是数值较大的正弯矩，双向板板底沿45°方向开裂，就是由主弯矩M_I产生的；主弯矩MⅡ矢量是与对角线相垂直的，并且在角部是数值较大的负值，双向板顶面角部垂直于对角线的裂缝就是由主弯矩M_Ⅱ产生的。

2.四边支承板的主要试验结果

1）板的竖向位移呈碟形，板的四角有翘起的趋势，因此板传给四边支座的压力沿边长是不均匀的，中部大、两端小，大致按正弦曲线分布。

2）在裂缝出现前，矩形双向板基本上处于弹性工作阶段，短跨方向的最大正弯矩出现在中点，而长跨方向的最大正弯矩偏离跨中截面。

3）两个方向配筋相同的正方形板，由于跨中正弯矩最大，板的第一批裂缝出现在板底中间部分，随后由于主弯矩M_I的作用，沿对角线方向向四角发展，如图2-39a所示，随着荷载不断增加，板底裂缝继续向四角扩展，直至因板的底部钢筋屈服而破坏。

4）当接近破坏时，由于主弯矩MⅡ的作用，板顶面靠近四角附近，出现垂直于对角线方向，大体上呈圆形的环状裂缝，这些裂缝的出现，又促进了板底对角线方向裂缝的进一步扩展；在两个方向配筋相同的矩形板板底的第一批裂缝，首先出现在中部，平行于长边方向，这是由于短跨跨中的正弯矩M₁大于长跨跨中的正弯矩M₂所致。随着荷载进一步加大，板底跨中裂缝逐渐延长，并沿45°角向板的四角扩展，如图2-39b所示，板顶四角也出现大体呈圆形的环状裂缝，如图2-39c所示。最终因板底裂缝处受力钢筋屈服而破坏。

图2-38 四边简支方板的主弯矩变化

图2-39 均布荷载下双向板的裂缝分布

四边支承双向板的受力特点及试验结果

相关推荐