结构计算简图及荷载分析方法

2025-09-30 理论教育版权反馈

【摘要】：对整体式梁板结构的板、次梁及主梁进行内力分析时，必须首先确定结构的计算简图。结构计算简图包括计算模型和计算荷载两个方面。结构计算模型的确定要考虑影响结构内力、变形的主要因素，忽略次要因素，使结构计算简图尽可能符合实际情况并能简化结构分析。图2-9 单向板肋梁楼盖平面、剖面及计算简图3.荷载取值与折算荷载荷载取值作用于梁板结构上的荷载可分为永久荷载（恒荷载）和可变荷载（活荷载）。

对整体式梁板结构的板、次梁及主梁进行内力分析时，必须首先确定结构的计算简图。结构计算简图包括计算模型和计算荷载两个方面。结构计算模型的确定要考虑影响结构内力、变形的主要因素，忽略次要因素，使结构计算简图尽可能符合实际情况并能简化结构分析。

1.计算假定

为了简化计算，通常引入如下假定：

1）梁板均为弹性杆件，其抗弯刚度为E_cI，E_c为混凝土的弹性模量，I为截面惯性矩。

2）梁、板的支座按表2-1采用。

表2-1 连续梁、板的支座

注：i_l、i_c分别为主梁和柱的线刚度。

3）在确定板传给次梁的荷载以及次梁传给主梁的荷载时，为了方便，可忽略板、次梁的连续性，每一跨都按简支梁来计算支座竖向反力。

假定2）中，有四点与实际情况不符：

1）端支座大多有一定的嵌固作用，故配筋时应在梁、板端支座的顶部放置一定数量的构造钢筋，以承受可能产生的负弯矩。当主要承受均布线荷载q时，通常取其负弯矩值为（-1/10～-1/12）ql²。

2）辊轴支座可自由转动的假定，实质上是忽略了次梁对板、主梁对次梁以及柱对主梁的约束。引起的误差将用折算荷载的方式来加以修正。

3）支座总是有一定宽度的，并不像计算简图中那样只集中在一点上，所以要对支座弯矩和剪力进行调整。

4）辊轴支座没有竖向位移，假定成滚轴支座实质上就是忽略了次梁的竖向变形对板、主梁的竖向变形对次梁的影响。

2.结构计算单元和计算模型

为了减少计算工作量，结构内力分析时，常常不是对整个结构进行分析，而是从实际结构中选取有代表性的某一部分作为计算的对象，称为计算单元。

整体式单向板梁板结构中，板结构计算单元可取1m宽的矩形截面板带作为板结构计算单元，在此范围内（图2-9中1m宽阴影表示）的楼面均布荷载（包括结构自重、抹灰荷载以及作用于板上的活荷载）便是该板带承受的荷载，这一负荷范围称为从属面积。

次梁结构通常取翼缘宽度为次梁间距l₁的T形截面带作为次梁结构计算单元。次梁承受板传来的均布线荷载以及次梁的结构自重、抹灰荷载。根据假定3），一根次梁的从属面积为次梁间距l₁的负荷范围。

主梁结构通常取翼缘宽度为主梁间距l₂的T形截面带作为主梁结构计算单元。主梁承受次梁传来的集中荷载以及主梁结构自重、抹灰荷载等。次梁传给主梁的荷载面积为l₁×l₂。一般主梁自重及抹灰荷载较次梁传递的集中荷载小得多，故主梁结构自重及抹灰荷载也可以简化为集中荷载。

依据假定，在现浇单向板肋梁楼盖中，板、次梁、主梁的计算模型为连续板或连续梁，其中次梁是板的支座，主梁是次梁的支座，柱或墙是主梁的支座，如图2-9所示。

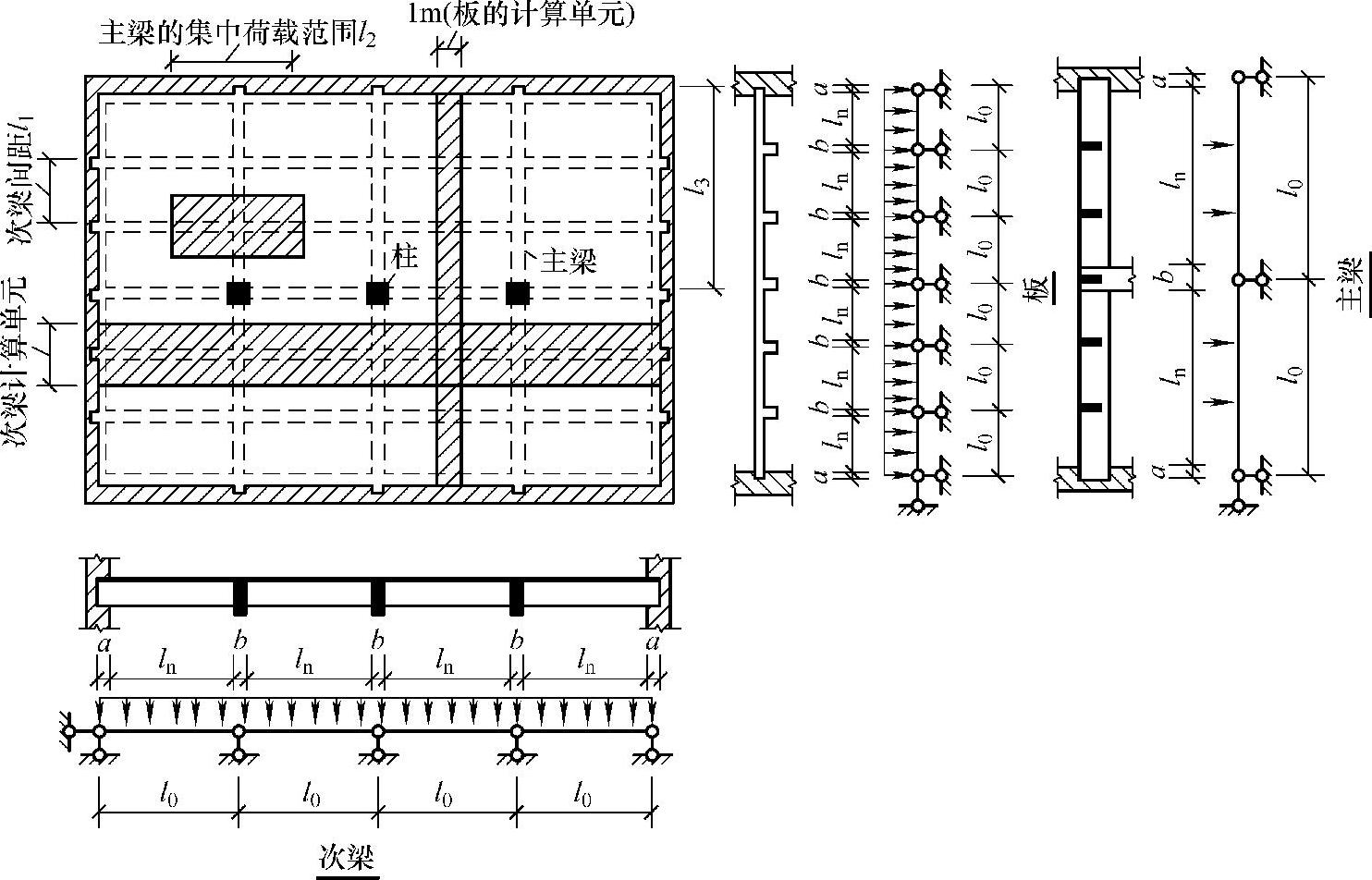
图2-9 单向板肋梁楼盖平面、剖面及计算简图

3.荷载取值与折算荷载

（1）荷载取值作用于梁板结构上的荷载可分为永久荷载（恒荷载）和可变荷载（活荷载）。永久荷载包括结构自重、地面及天棚抹灰、隔墙及永久性设备等荷载。可变荷载包括人群、货物荷载及雪荷载、屋面积灰荷载、施工活荷载等。可变荷载的分布通常是不规则的，在工程设计中一般折算成等效均布荷载。作用于板、梁上的活荷载在一跨内均按满跨布置，不考虑半跨内活荷载作用的可能性。永久荷载、可变荷载的标准值及荷载分项系数，详见GB 50009—2012《建筑结构荷载规范》。

在设计民用建筑梁板结构时，应注意楼面可变荷载值的折减问题，梁的负荷面积较大时，可变荷载全部满载并达到标准值的概率小于1，故计算梁时适当降低可变荷载数值更为符合实际，可变荷载的折减系数值详见《建筑结构荷载规范》，其折减系数即为可变荷载满载并达到标准值的概率。

（2）折算荷载整体式梁板结构中，板、梁和柱是整体浇筑在一起的，板支承于次梁，次梁支承于主梁，主梁支承于柱。因此，次梁对板、主梁对次梁、柱对主梁将有一定的约束作用，上述约束作用在结构分析时必须予以考虑。

例如，单向板在隔跨布置的活荷载作用下，支座次梁将发生转动，次梁由于两端固定在主梁上，将产生扭转抵抗而约束板在支座处的转动，其转角为θ′，如图2-10b所示。同样的约束作用也发生在次梁与主梁、主梁与柱之间。

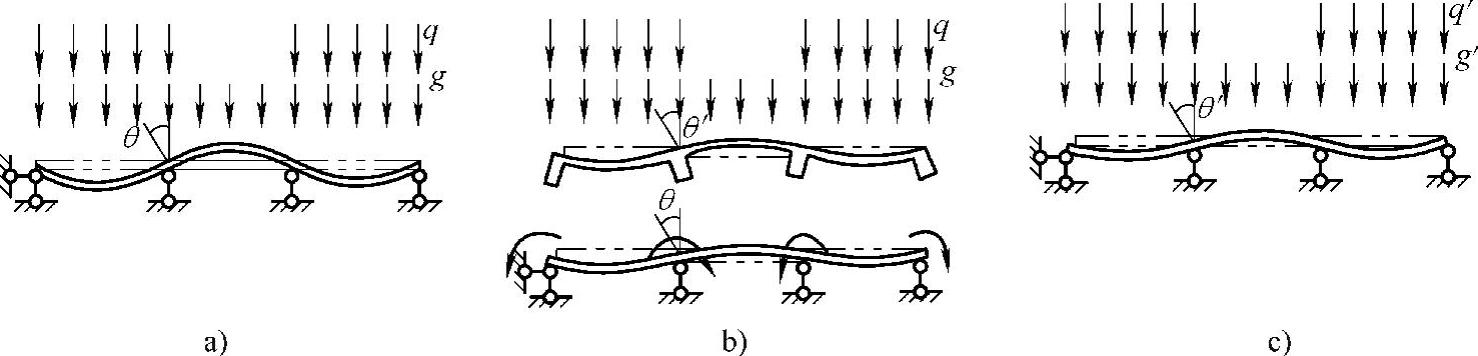
图2-10 次梁抗扭刚度对板的影响

为简化计算，假定结构的支承条件为铰支座，在上述荷载作用下结构支座处转角为θ，且θ＞θ′，如图2-10a所示。由此引起的误差需在结构分析时，通过调整结构恒荷载与活荷载的比例加以解决。由结构力学可知：多跨连续梁、板在均布的恒荷载作用下，中间支座截面转角值很小；而在隔跨布置的活荷载作用下，中间支座截面转角较大。为使铰支座的连续梁、板结构支座转角接近θ′，可采用增大恒荷载g值，减小活荷载q值的方法来解决上述约束作用引起的误差，如图2-10c所示。由于次梁对板的约束作用较主梁对次梁的约束作用大，故对板和次梁荷载采用下述的荷载调整方法，调整后折算荷载值可取为

连续板

次梁

式中 g、q——恒荷载、活荷载设计值；

g′、q′——折算恒荷载、活荷载设计值。

当主梁的线刚度与柱的线刚度比值大于5时，柱对主梁的约束作用较小，故对主梁荷载不作调整。

4.结构的计算跨度(https://www.chuimin.cn)

整体式梁板结构中，梁、板计算跨度是指单跨梁、板支座反力的合力作用线间的距离。支座反力的合力作用线的位置与结构刚度、支承长度及支承结构材料等因素有关，精确地计算支座反力的合力作用线的位置是非常困难的，因此梁、板的计算跨度只能取近似值。

（1）按弹性理论计算

1）对于单跨板和梁：

两端搁支在砖墙体上的板l₀=l_n+a≤l_n+h （2-7）

两端与梁整体连接的板l₀=l_n+b （2-8）

单跨梁l₀=l_n+a≤1.05l_n （2-9）

2）对于多跨连续板和梁：

边跨

且

中间跨l₀=l_c （2-13）

且l₀≤1.1l_n（板）（2-14）

l₀≤1.05l_n（梁）（2-15）

（2）按塑性理论计算按塑性理论计算时，多跨连续梁板的跨度由塑性铰的位置确定。

1）对于连续梁：

当两端与梁或柱整体连接时l₀=l_n （2-16）

当两端搁支在墙上时l₀=min（1.05l_n，l_c）（2-17）

当一端搁支在墙上，一端与梁整体连接时

2）对于连续板：

当两端与梁整体连接时l₀=l_n （2-19）

当两端搁支在墙上时l₀=min（l_n+h，l_c）（2-20）

当一端搁支在墙上，一端与梁整体连接时

式中 l_c——支座中心线之间的距离；

l₀——梁板的计算跨度；

l_n——梁板的净跨度（见图2-9）；

h——板的厚度；

a——梁、板在墙体上的支承长度（见图2-9）；

b——梁、板的中间支座宽度（见图2-9）。

5.结构的计算跨数

依据前述假定，连续梁板的计算简图如图2-11b所示。结构计算中对于等跨度、等刚度、荷载和支承条件相同的多跨连续梁板，经结构内力分析表明：除端部两跨内力外，其他所有中间跨的内力都较为接近，内力相差很小，在工程结构设计中可忽略不计。因此，所有中间跨的内力和配筋都可按第三跨处理，如图2-11c所示，即当结构实际跨数多于五跨时，可按五跨进行内力计算，如图2-11d所示。

对于跨数超过五跨的连续梁板，当各跨荷载相同，且跨度相差不超过10%时，可按五跨连续梁板进行计算。

对于跨数小于五跨的多跨连续梁板，按实际跨数计算。

对于跨度、刚度、荷载或支承条件不同的多跨连续梁板，应按实际跨数进行结构分析。

结构计算简图及荷载分析方法

相关推荐