单元刚度矩阵是基于杆单元局部坐标系的，以杆轴线为x 轴，这样所有的单元都具有相同的单元刚度矩阵的形式。可以采用坐标变换的方法，将局部坐标系下的单元刚度矩阵转换至整体坐标系中。图9-4整体坐标系中的单元刚度矩阵K e。......
2023-08-30
连续梁整体刚度矩阵-结构力学
【摘要】：λ e中的元素决定了单元刚度矩阵中的各元素在结构刚度矩阵中的位置，故将 λ e称为单元 e 的定位向量。对于式和式有 试用直接刚度法建立如图 9-6 所示连续梁的结构刚度矩阵，并计算各杆的杆端弯矩。图9-6单元刚度矩阵和定位向量。
结构计算必须满足平衡条件和变形协调条件。矩阵位移法在单元分析的基础上，利用结构的变形协调条件和平衡条件建立结构刚度方程，得到结构刚度矩阵。研究结构刚度矩阵形成的规律，便可直接形成结构刚度矩阵的方法。
如图9-5 所示两跨连续梁分为两个单元，三个结点，单元编号为①、②，结点编号为 1～3，采用图示整体坐标系，其中单元坐标系与整体坐标系相一致。现取结构的结点位移列向量为：
其中 Δ（ii=1, 2, 3）代表第 i 个结点位移，以顺时针为正。
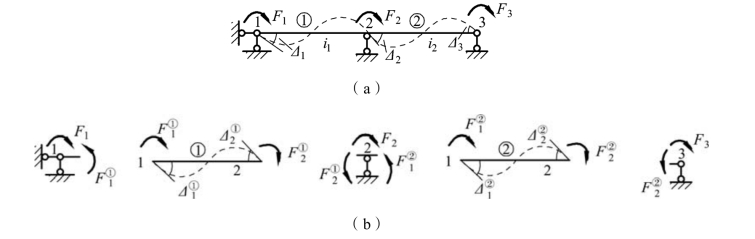
图9-5 连续梁
相应的结点荷载是附加约束上的集中力偶 F1， F2， F3。它们构成整体坐标系下结点荷载的列向量：
其中Fi代表与第i 个结点角位移相应的荷载，与Δi方向一致时为正。下标中的1，2，3是对结点位移和结点荷载在整体坐标系中统一编排的数码，称为总码。
为了导出结点荷载列向量 F 与位移列向量Δ 之间的关系式，应考虑结点的力矩平衡方程条件和结点与杆端的变形协调条件。取如图9-5 所示结点为隔离体，建立相应的平衡方程。即
写成矩阵：
对于单元①：
其单元①刚度矩阵为：
式中标注在单元刚度矩阵旁用整体码表示行码和列码。
对于单元②：
其单元②刚度矩阵为：
对结构进行整体分析，引入位移条件，即
引入平衡条件，即
将式（9-21）和式（9-23）代入式（9-25）可得
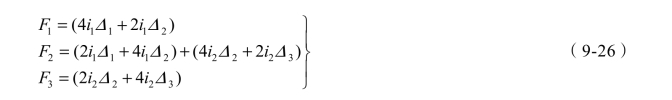
将上述方程写成矩阵的形式，即
简写为：
式中的K 就是结构刚度矩阵，即
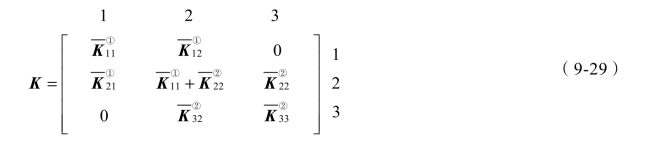
由式（9-29）可以看出，结构刚度矩阵中的各元素都是由各单元刚度矩阵的相关元素组成，单元刚度矩阵元素在结构刚度矩阵中的位置，由单元在整体坐标系中所对应的总码决定。根据元素所对应的总码，可将单元刚度矩阵中的相关元素直接形成结构刚度矩阵。
上述先对单元刚度矩阵换码，再按总码表示的列码和行码分别将各元素置于结构刚度矩阵的相应位置，直接形成结构刚度矩阵的方法称为直接刚度法。而在形成结构刚度矩阵之前，已考虑结构位移边界条件（如结点线位移为零，固定端转角为零）的直接刚度法称为先处理法。
将所得结构刚度矩阵代入式（9-28)，得结点位移，即
根据上式求得结点位移后，根据变形协调条件将杆端位移代之以相应的结点位移，即可计算出各单元的杆端弯矩。
各单元刚度矩阵换码后才能用直接刚度法形成结构刚度矩阵。换码后矩阵上方从左往右，右侧从上往下，总码的排列是完全相同的，所以可将其写成列向量的形式并用 λ e表示。 λ e中的元素决定了单元刚度矩阵中的各元素在结构刚度矩阵中的位置，故将 λ e称为单元 e 的定位向量。
对于式（9-21）和式（9-23）有
【例题 9-2】 试用直接刚度法建立如图 9-6 所示连续梁的结构刚度矩阵，并计算各杆的杆端弯矩。
解：（1）编号。
单元编号为①、②；结点位移分量的总码分别编号为 0、1、2。左端为固定端支座，结点无转角位移，编号为0；杆件轴线的箭头表示单元坐标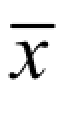
的方向。
图9-6
（2）单元刚度矩阵和定位向量。
单元①的刚度矩阵及定位向量为：
单元②的刚度矩阵及定位向量为：
（3）整体刚度矩阵为：
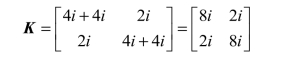
（4）荷载列向量为：
（5）基本方程：
即
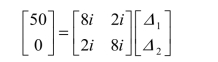
（6）解方程可得：
根据各单元定位向量，从解得结点位移中确定相应的杆端位移，根据单元①和②的刚度矩阵，确定单元①和②的杆端弯矩如下。
单元①：
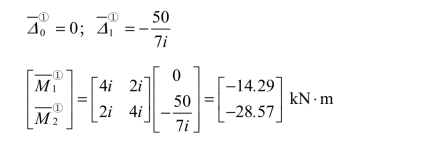
单元②：
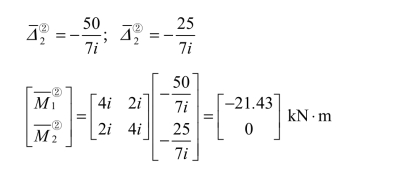
所得结果满足结点 2 的力矩平衡条件，故知计算结果正确。
有关结构力学的文章
- 详细阅读
-
混凝土连续梁板内力分析方法详细阅读
在等截面的连续梁板结构中，若结构各截面配筋相同，即结构的Mu相同，则结构截面内力最大者，即为结构的控制截面。由等截面多跨连续梁板结构分析与设计可知：梁、板的各支座截面及各跨的跨中截面为结构的控制截面。图2-12为五跨连续梁单跨布置活荷载时的弯矩图和剪力图。现以承受均布线荷载的五跨连续梁的弯矩、剪力包络图来说明。......
2023-08-30
-
3.2结构力学：多跨静定梁的内力计算详细阅读
图3-6多跨静定梁是由若干单跨静定梁相互用铰连接起来的，通常有两种基本形式。图3-82.多跨静定梁的内力计算从受力分析来看，由于基本部分直接与地基组成几何不变体系，因此它能独立承受荷载而维持平衡。......
2023-08-30
-
用位移法计算连续梁与超静定刚架详细阅读
位移法计算连续梁及超静定刚架一般步骤如下：确定基本未知量和基本结构。用位移法计算时，只有节点转角基本未知量，故仅需建立刚节点处的力矩平衡方程，即可求解出全部未知量，进而计算杆端弯矩，绘制出内力图。此连续梁只有一个刚节点B的转角位移θB，如图15-32所示。列各杆杆端弯矩计算式。用位移法计算图15-34所示的超静定刚架，并作出弯矩图。......
2023-08-26
-
混凝土连续梁板塑性理论内力分析方法详细阅读
这种不一致现象主要是由钢筋混凝土的受弯塑性变形引起的，称为塑性内力重分布。需要特别注意的是，塑性铰的转动能力有一定的限度，这会影响塑性内力重分布的程度。......
2023-08-30
-
简支梁的绝对最大弯矩和内力包络图-《结构力学详细阅读
据此可以判断，在荷载组中部的几个集中荷载作用的截面，发生绝对最大弯矩的可能性最大。经验表明，在通常情况下产生简支梁绝对最大弯矩时的临界荷载 FK就是使跨中截面产生最大弯矩时的临界荷载。试求简支梁的绝对最大弯矩，并与跨中截面 C 的最大弯矩相比较。包络图分为弯矩包络图和剪力包络图。......
2023-08-30
-
用力矩分配法计算连续梁和无侧移刚架设计技巧详细阅读
上节用只有一个刚结点的结构介绍了力矩分配法的基本概念。对于具有两个以上刚结点的结构也可用力矩分配法进行计算。多结点力矩分配法的计算步骤如下：求出汇交于各结点每一杆端的力矩分配系数μij，并确定其传递系数Cij。固定刚结点B和C，各杆的固端弯矩为其余各固端弯矩均为零。刚结点B的约束力矩除固端弯矩外，还包括传递过来的传递弯矩，即所以传递弯矩为进行第二轮计算。用力矩分配法作图16-8所示刚架的弯矩图。......
2023-06-16
-
加劲梁参数分析及索塔刚度对位移影响详细阅读
图7.24弹性模量变化对加劲梁位移响应的影响图7.25抗弯惯性矩对加劲梁位移响应的影响表7.14加劲梁参数对位移响应的影响上述分析结果表明，加劲梁的弹性模量与抗弯惯性矩对动力响应有一定的影响，且二者的影响值和规律几乎相同。图7.29索塔刚度对加劲梁位移的影响为了分析索塔刚度对加劲梁位移动力可靠度的影响，选取索塔的弹性模量Et为变量，分析Et增加或减小10%对加劲梁动力可靠度的影响。......
2023-09-19
相关推荐